3.3. Метод Ньютона.

Пусть снова задано уравнение f(x)=0. Запишем его тождественно в виде ,

где , и положим .

Пусть х_к – некоторое приближение к корню х*. Для ускорения сходимости итераций желательно, чтобы был как можно меньше. Положим

Отсюда находим, что . Подставляя в исходное уравнение, получаем рекуррентную формулу:

, . (11)

Это и есть итерационная процедура Ньютона.

Метод Ньютона известен и под другим названием: метод касательных. Дадим графическую иллюстрацию данного метода.

Пусть и строго выпукла (т.е. ). Пусть, кроме того, - единственный корень функции на промежутке .

В качестве начального приближения возьмем точку , такую, для которой . Проведем через точку на плоскости касательную к кривой . Запишем уравнение касательной: . В качестве следующего приближения возьмем точку , в которой . Отсюда находим

. Далее в точке графика проводим новую касательную, и т.д. В результате получаем итерационную процедуру Ньютона (11).

Метод касательных проиллюстрирован на рис.3.2.

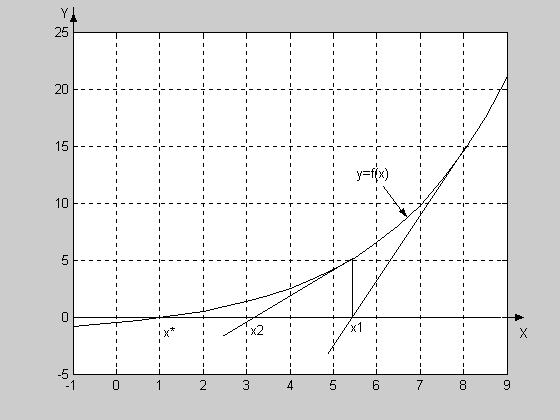
Рис.3.2. Графическая иллюстрация метода Ньютона (метода касательных). Начальная точка x₀ = 8. Точное значение корня x* = 1. x₁ и x₂ – два последовательных приближения к корню, полученные с помощью касательных.

Исследуем условия сходимости метода Ньютона.

Теорема 3.5. Пусть , на , и имеет единственный действительный корень на . Тогда , такое, что на множестве

процедура Ньютона (1) сходится к точке со скоростью геометрической прогрессии, а в некоторой малой окрестности точки x^* и с квадратичной скоростью.

В силу непрерывности функций на [a,b], обе производные ограниченыпоэтому , причем по условию.

Заметим, что итерационная процедура (11) равносильна методу простых итераций для уравнения

(12)

Очевидно, что является неподвижной точкой функционального оператора , называемого операторной функцией Ньютона-Рафсона. Проверим условия сжатости данной функции. Для этого вычислим и оценим производную . Имеем:

.

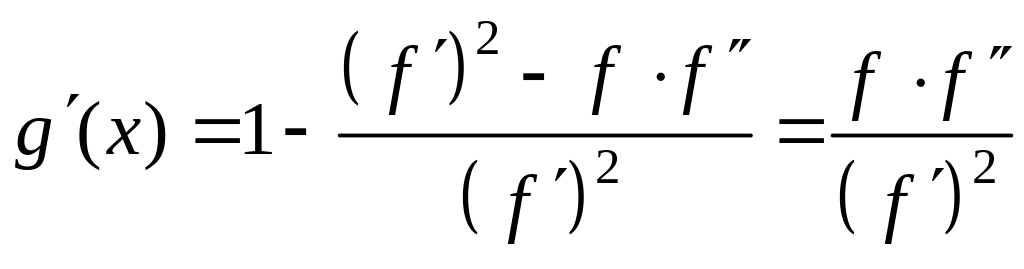Оценивая полученное равенство по модулю, и учитывая условия теоремы, получим

(13)

Поскольку - корень уравнения , то, как следует из неравенства (13),

и близка к нулю в некоторой малой окрестности точки , где и следует ожидать выполнения условия сжатости.

Запишем формулу конечных приращений Лагранжа

.

Оценивая по модулю, получаем

.

Подставляя эту оценку в (13), получаем:

.

Условие сжатости будет, очевидно, выполнено, если

. (14)

Обозначив , получаем конкретизацию окрестности , где выполняется одно из условий сжатости. Пусть теперь найдено -е приближение к корню .

Так как по условию теоремы непрерывна на , то справедливо тэйлоровское разложение функции с центром в точке с остаточным членом в форме Лагранжа

Положим в последнем равенстве :

.

Выражая отсюда , получим:

(15)

Вычтем (15) из (11):

;

Оценивая последнее равенство по модулю, получаем:

(16)

Продолжим далее оценку по модулю, используя (14):

.

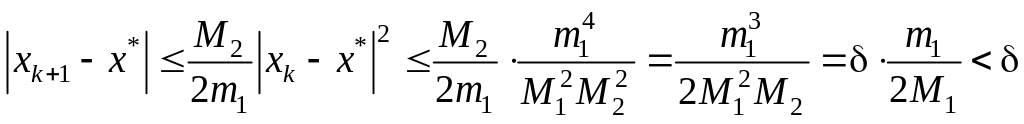Таким образом, если , где определяется из неравенства (14), то точка . Следовательно, выполняется и второе условие теоремы 3.4, а значит последовательность сходится к корню со скоростью геометрической прогрессии (т.е. линейно). Далее из неравенства (16) следует, что как только при некотором выполнится условие , так в дальнейшем, при сходимость становится квадратичной:

.

Пример 3. Вычислить с точностью до 3-х верных знаков после запятой.

Положим . Заметим, что , т.е. – строго выпукла всюду. Согласно процедуре Ньютона (11),

.

В качестве начального приближения возьмем . На третьей итерации заданная точность достигается:

x₃=3,60555»3,6056 ( точное значение .

Метод Ньютона в многомерном случае.

Пусть задана система нелинейных уравнений

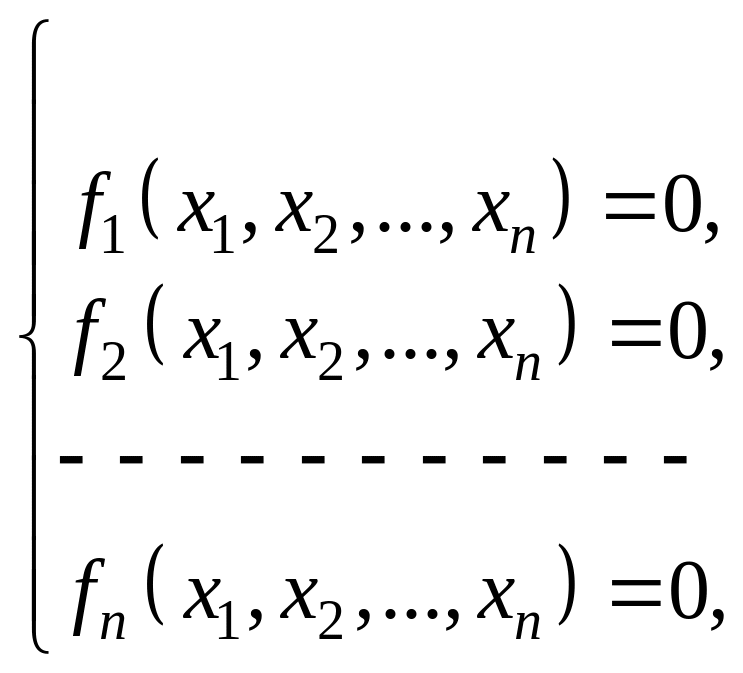
или в более компактной форме: f(x)=0, где ─ -мерная вектор-функция (вектор-столбец).

Для реализации метода решения и исследования сходимости необходимо, чтобы функции были достаточно гладкими, например, , где .

Рассмотрим i-ое уравнение системы: и пусть - некоторое приближение к корню , полученное на k-ой итерации.

Разложим функцию в многомерный ряд Тейлора в точке :

,

(17)

где

-

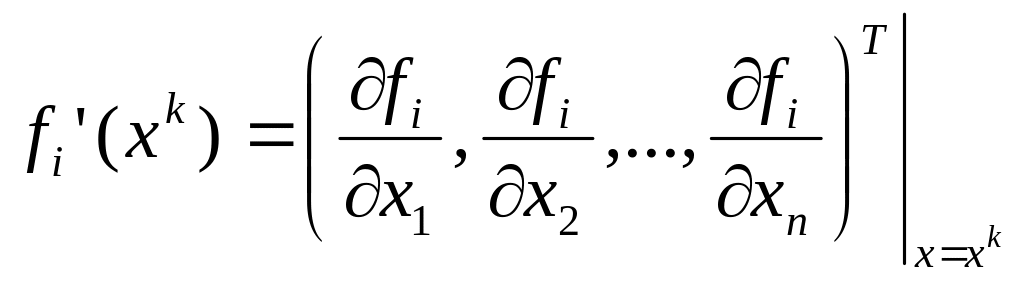- вектор-градиент функции в точке , а - скалярное произведение векторов a и b. Пренебрегая остаточным членом в (17), положим

или в более компактной матричной форме:

,

(18)

где

-

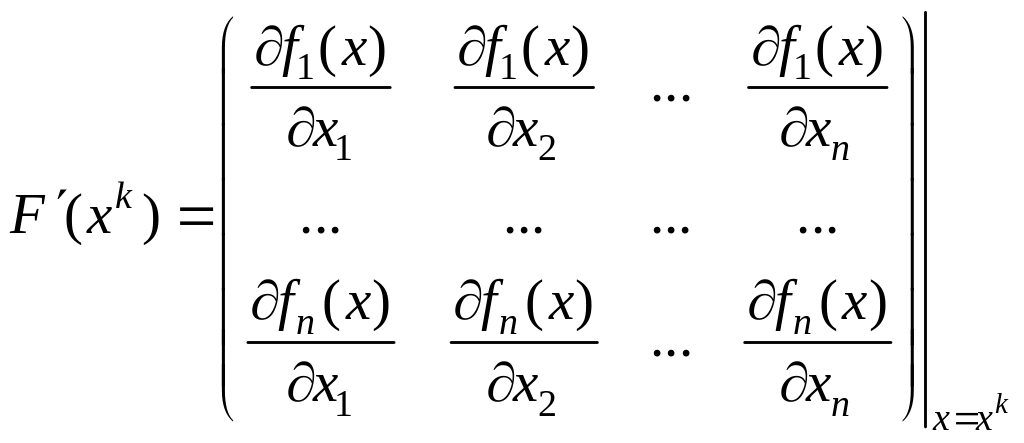- так называемая матрица Якоби первых производных в точке .

Пусть . Разрешим систему линейных алгебраических уравнений (18) относительно x:

И положим :

(19)

Векторное уравнение (19) представляет собой итерационную процедуру Ньютона в многомерном случае. Для ее запуска необходимо задать начальную точку . Однако при произвольном выборе начальной точки нельзя гарантировать сходимость процедуры Ньютона. Вопрос о сходимости (19) в теоретическом плане более сложный, чем тот же вопрос о сходимости метода Ньютона в одномерном случае. Рассмотрим некоторые основные моменты проблемы исследования сходимости процедуры (19).

Прежде всего отметим, что для реализации метода Ньютона необходимо, чтобы матрица Якоби была невырождена в некоторой окрестности точки . Тогда обратная матрица существует в этой окрестности. Аналогично одномерному случаю, процедуру (19) можно рассматривать как итерационный поиск неподвижной точки для уравнения

,

где - -мерная оператор-функция. Можно показать, что . Поэтому, как и в одномерном случае существует окрестность точки , в которой оператор-функция является сжимающим оператором с некоторой константой сжатия , тем меньшей, чем ближе точка к точке (в эвклидовой норме). Поэтому о характере сходимости многомерного метода Ньютона справедливы утверждения, аналогичные одномерному случаю.

Например, если - строго выпукла в G, и начальное приближение выбирается достаточно близко к , то итерационная процедура Ньютона (19) сходится с линейной скоростью, а, начиная с некоторого номера, - и с квадратичной скоростью.

Замечание. Строгую формулировку достаточных условий сходимости метода Ньютона в многомерном случае можно найти в цитируемой литературе (см., например, [2]). На практике эти условия, как правило, проверить чрезвычайно сложно. Поэтому при работе на компьютере (например, в пакете MATLAB) используют метод проб и ошибок при выборе начальной точки . На начальном этапе важно найти так называемую зону притяжения, т.е. такую область , что при выборе процедура (19) сходится.

Пример 4. Задана система уравнений:

Взяв в качестве начального приближения точку , выполнить одну итерацию по методу Ньютона.

Ответ: . Точное решение: .