3.2. Метод простых итераций для функциональных уравнений.
Теорема 3.3. Пусть
(одномерный
случай) и задана функция f(x),
удовлетворяющая условиям:
1)
условие Липшица с константой на отрезке [a,b];
2)
|
(1) |
-
.Тогда оператор f(x) - сжимающий и уравнение f(x)=х имеет единственную неподвижную точку, которую можно найти методом простых итераций:
.
Действительно,
определим
.
Следовательно, выполняется условие
Липшица из теоремы 3.2, откуда и следует
результат.
Теорема 3.4. Пусть
,
причем выполнены условия:
1) ;
2)
|
(8) |
Тогда оператор
f(x)
является сжимающим, и справедливо
утверждение теоремы 3.1, т.е. последовательность
сходится к единственному коню уравнения
.
Пусть
,
тогда
,
согласно условию 1) теоремы. Далее по
индукции устанавливаем, что все члены
последовательности
принадлежат
.
Пусть
.
Согласно теореме о среднем
,
.
Оценим это неравенство по модулю:
согласно условию
2) теоремы.
Таким образом, выполняются все условия теоремы 3.3., откуда и следует результат.
Рассмотрим задачу
поиска корней уравнения
.
Пусть известны границы для единственного
корня этого уравнения и мы хотим найти
этот корень методом итераций. Если
удастся привести уравнение к виду
x=f(x),
так чтобы
выполнялись условия теоремы 3.3 или
теоремы 3.4, то в этом случае можно будет
применить метод итераций. Такое
преобразование, вообще говоря, не
единственно, причем главная трудность
заключается в определении того замкнутого
ограниченного множества S
(а в одномерном случае – отрезка [a,b]),
для которого помимо условия сжатости,
выполняется условие
.
Лемма 3.1. Определим
множество
-
замкнутый r-“шар”
с центром в точке х0
(в одномерном случае – отрезок). Пусть
оператор Т
- сжимающий на S
и выполняется следующее условие:
|
(9) |
Тогда для любой
точки
выполняется:
.
Достаточно
доказать, что
Имеем:
{неравенство
треугольника}
.
Пример 1. Решить уравнение
с точностью
.
Приведем уравнение к виду:
|
(10) |
Г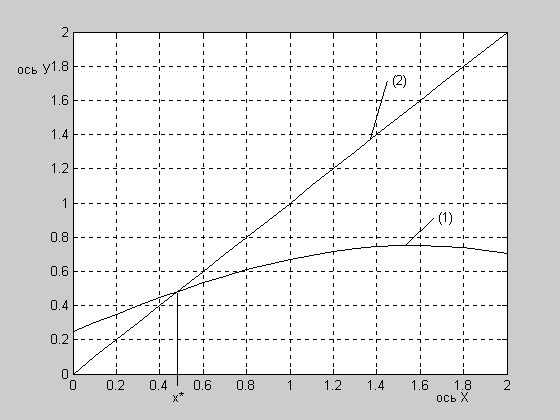
рафическое
решение уравнения (10) приведено на
рисунке 3.1.
Рис. 3.1. Графическое решение уравнения
(10). Кривая (1) - график функции
.
Кривая (2) - график функции
.
Найдем первую
производную:
.
При
имеем:
(значение
можно использовать в итерациях). Можно
улучшить оценку для
,
если заметить, что по графику на рис.3.1
.
Но это значение константы сжатия следует
подтвердить выполнением условия (9)
леммы 3.1.
Для простоты
положим
=0,5
и оценим радиус “шара” r,
взяв в качестве начальной точки
.
Тогда получим:
;
.
Таким образом, если положить
,
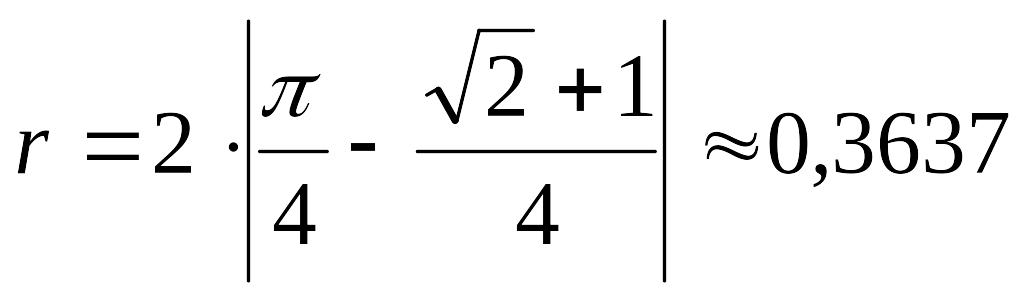то условие (9) выполняется. Последовательно находим:
Продолжаем
процедуру, пока 4 значащие цифры после
запятой не установятся. При
придется
сделать 10 итераций, при этом х*=х10=0,4816.
Пример 2. Решить
уравнение
F(x)=tg
x
– x=0,
xÎ[
;
].
Решить самостоятельно: построить график, затем сделать замену переменных:
x=
+arctg
y
и привести уравнение к виду:
y=
+arctg
y=f(y),
показать, что данное уравнение
удовлетворяет принципу сжатых отображений.
Оценить α и запустить процедуру для ε
= 0,001.