8. Порівняння чисел різними способами (Змоделюйте фрагмент уроку)

На підставі порівняння сукупностей об’єктів способом утворення пар учні знайомляться з рівночисельними та нерівночисельними множинами, зі знаками «рівно», «не рівно». Коли порівнюються рівночисельні сукупності або рівні числа, з’ясовується відношення рівності, то ставиться знак «=». Для того, щоб пояснити учням, чому саме цей знак обраний для позначення рівності, вчитель звертає увагу на те, що цей знак складається з двох відрізків однакової довжини.

У подальшому навчанні діти знайомляться з написанням знака порівняння: «більше», «менше». Зазначимо, що, пояснюючи запис результату порівняння за допомогою знаків «більше», «менше», треба звернути увагу школярів на те, що це один і той же знак, тільки перекинутий. Знак ставиться так, щоб більше число знаходилося з того боку, де відстань між кінцями більша. Або можна застосувати аналогію з пташками: мама-пташка годує маленьких пташенят із дзьобика, тому до меншого числа знак ставимо «дзьобиком».

С

3 < 4

посіб утворення пар. Наприклад, треба порівняти числа 3 і 4. Діти викладають на парті стільки кружечків, скільки вказує цифра «3»; під кружечками викладають стільки трикутників, скільки вказує цифра «4»; складають пари з кружечків і трикутників; з'ясовують, які фігури лишилися без пари – їх більше; яких фігур не вистачило для утворення пар – їх менше. Запис нерівності діти читають двома способами: три менше чотирьох. Чотири більше трьох.

Цей спосіб порівняння чисел використовується в період ознайомлення з числами першої п’ятірки.

С

5 < 7

посіб порівняння за місцем числа в натуральному ряду. Порівняння здійснюються на підставі застосування правила: «Число, яке йде при лічбі раніше (пізніше) даного числа, завжди менше (більше) цього числа». Наприклад, треба порівняти числа «5» та «7»: число «5» при лічбі називається раніше, ніж число «7», тому «5» менше «7»; число «7» при лічбі називається пізніше, ніж «5», тому «7» більше за «5».

Л

4 < 5

огічний спосіб міркування здійснюються на підставі знання складу чисел. Наприклад, треба порівняти числа «5» та «4»: число «5» – це «4» та ще «1», «4» та ще «1» більше чотирьох, тому п’ять більше чотирьох. Порівняємо числа «4» та «5»: «4» – це «5» без 1-го, «5» без 1-го менше п’яти , тому «4» менше 5-ти.

9. Вивчення складу чисел (Змоделюйте фрагмент уроку)

Вивчення складу чисел за чинною програмою розглядається як етап, що допомагає здійснити підготовку до розуміння дій додавання і віднімання та засвоєння таблиць додавання і віднімання в межах 10. Ознайомлення зі складом числа проводиться на предметній основі. З цією метою доцільно використовувати два різновиди вправ: розгляд окремих випадків складу числа і розгляд впорядкованої сукупності пар чисел, на які можна розкласти число.

Р

озглянемо методику ознайомлення зі складом числа «5». Учитель пропонує учням поділити робоче місце парти на дві частини – праву та ліву і взяти п’ять зелених кружечків та розташувати їх ліворуч. Пересуваючи по одному кружечку праворуч, визначаємо їх кількість окремо ліворуч та праворуч, а також загальну кількість; виходячи з цього, робимо висновок про те, що ці числа складають дане число; записуємо випадок складу числа в таблиці:

5

4 1

2 3

1 4

Записуючи склад числа «5», ми почнемо з випадку утворення числа «5» з попереднього числа «4» і «1», а потім, подумки пересуваючи по одному кружечку, відтворимо і всі випадки складу числа «п’ять».

значення

частки

5

4 1

І

люструвати склад чисел можна за допомогою кругів, що обертаються. Учитель вирізає з картону два однакові круги і кожний з них ділить, наприклад, на 5 сегментів (стосовно складу числа, що вивчається); у центрі кожного сегменту розташовується якийсь малюнок – у першому крузі, наприклад, червоного кольору, а в другому – зеленого.

У кожному крузі робимо розріз по радіусу. У цей розріз вставляються круги один в один , що дозволяє їх обертати.

Для запам’ятовування складу чисел корисними є завдання на складання «будиночків», «машинок», «потягів» зі складом чисел. Треба зазначити, що, враховуючи дані психологічної науки стосовно підвищення ефективності сприймання молодших школярів, ці таблиці корисно розташовувати горизонтально:

7	3	2	7	3	4	6
1	5	6	1	5	4	2

8

3	2	1	5	4	6
4	5	6	2	3	1

7

Для засвоєння складу чисел корисно застосовувати картки типу «доміно»: спочатку учні виконують прості вправи – визначають, скільки точок праворуч, скільки ліворуч, скільки точок усього. Далі дітям пропонується знайти лише ті картки, які ілюструють число. Наприклад: з карток «доміно» виберіть ті, що ілюструють склад числа, наприклад «5»:

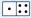
Після ознайомлення з дією додавання склад числа розглядається як подання його у вигляді суми двох доданків. А після введення конкретного змісту дії віднімання учні за картками «доміно» складають не лише дві рівності на додавання, а й дві – на віднімання. Таким чином, відбувається пропедевтика переставної властивості додавання та взаємозв’язку між діями додавання і віднімання. Наприклад: 2 + 3 = 5. Зліва 2 точки, справа 3 точки; об’єднуємо точки зліва направо, буде 5 точок. 3 + 2 = 5 Справа 3 точки, зліва 2 точки; об’єднуємо точки справа наліво, отримаємо 5. 5 – 2 = 3. Всього 5 точок, виключили 2 точки (можна прикрити їх рукою), отримаємо 3 точки. 5 – 3 = 2. Всього 5 точок¸ виключили 3 точки, залишилось 2 точки.

Корисні завдання на заповнення пропусків у складі чисел і запис на цій основі рівності на додавання та віднімання:

5	+	1	=	6
3	+	3 3	=	6
1	++	5	=	6
4	+	2	=	6
2	+	4	=	6
.
.

6	-	5	=	1
6	-	3	=	3
6	-	1	=	5
6	-	2	=	4
6	-	4	=	2

6 – це 5 і 1.

6 – ціле. 5 і 1 – його частини.

Об’єднуємо частини в ціле: 5 + 1 = 6. Виключаємо з цілого його першу частину, лишається друга частина:

6 – 5 = 1.

6

5	1
3	3
1	5
4	2
2	4

Тема «Числа першого десятка» закінчується вивченням числа «нуль». Поняття про число «нуль» вводимо, як результат віднімання однакових чисел. Спосіб отримання числа «нуль» полягає у вилученні із множини всіх її елементів і запису дій над числами. Наприклад:

На гілці було 2 листочки. Подув вітер, і один листочок упав на землю. Скільки листочків залишилося? (1) Як знайшли? (Ми від 2-х відняли 1, отримали 1: 2 – 1 = 1) Ще раз подув вітер і останній листочок упав. Скільки листочків залишилося на гілці? (Нічого ) А як це записати? (Треба від 1 відняти 1.) «Нічого» – це означає пуста множина предметів, тобто множина, в якій немає жодного елемента; в математиці численність такої множини відповідає числу «нуль». Тому запишемо: 1 – 1 = 0.

А якщо б вітер зірвав відразу два листочки, скільки б залишилося листочків на гілці? (2 – 2 = 0) Учні наводять приклади, коли в результаті отримаємо число нуль: 4 – 4, 14 – 14, 100 – 100 .

Далі з’ясовується, коли ми отримуємо нуль? При виконанні якої арифметичної дії? (При відніманні.) Чи завжди при відніманні ми отримуємо нуль? (Ні) А коли при відніманні отримуємо нуль? (Лише тоді, коли віднімаємо однакові числа). Школярі роблять висновок: при відніманні однакових чисел отримуємо в результаті число «нуль».

Число «нуль» позначається цифрою, яка називається так само – «нуль – 0».

При вивченні чисел від 0 до 9 необхідно приділяти увагу формуванню узагальненого поняття про лічильну одиницю. Для цього при розгляданні кожного числа включаються вправи на лічбу однакових груп предметів (вивчаючи число 2 – лічать пари предметів, число 3 – трійки предметів, число 4 – четвірки предметів, 5 – п’ятірки предметів й так далі). Виконуючи такі вправи, діти помічають, що корисно застосовувати групування предметів при лічбі, так можна порахувати велику кількість предметів; але результат лічби залежить від обраної лічильної одиниці.

Наприклад, на набірному полотні стоять 4 малюнки з трійками коней. Діти малюють чотири трійки точок і потім ведуть лічбу по-різному: можна сказати, що тут 4 трійки коней, або 2 шестірки, або 12 коней. Така робота готує учнів до введення десятка як складеної лічильної одиниці.

Підсумовуючи слід зазначити, що, основні питання нумерації за чинною навчальною програмою для учнів початкової школи розглядаються в межах конкретного числа, що вивчається.