Практическая работа № 17. Приёмы математического анализа, математической статистики и теории информации Вариант №1
Цель работы – установить взаимосвязи между различными явлениями, отображаемыми на географических картах, используя корреляционный анализ.
Общие сведения
В статистических исследованиях по картам нашли применение основные приемы математической статистики. Это, прежде всего, изучение характера распределения явлений, изображенных на карте. Такие исследования связаны с вычислением разного рода обобщающих статистик, к которым относятся средние величины и показатели разнообразия.
Самое широкое применение в картографических исследованиях находит аппарат корреляционного анализа, позволяющий установить взаимосвязи между различными явлениями по одной карте или серии карт. Форма и теснота связей между двумя явлениями, имеющими на карте количественную характеристику, оцениваются с помощью коэффициента корреляции r или корреляционного отношения (для случая криволинейной связи). Теория корреляции позволяет установить также взаимосвязи между несколькими явлениями с помощью коэффициента множественной корреляции R.
Вычисление коэффициента корреляции и построение поверхностей регрессии и отклонений. Для характеристики взаимосвязи между двумя явлениями, изображенными на двух разных картах, используется безразмерная величина, называемая коэффициентом корреляции r. Он вычисляется, если связь между явлениями А и В близка к прямолинейной.
Числовые
значения коэффициента корреляции
.
Если r = 1 или r = –1, то
это указывает на полную прямую или
обратную связь. Когда
,
связь между явлениями отсутствует. При
связь считается существенной.
Для расчета показателя связи с обеих карт необходимо получить две выборки. С этой целью на карты строго координированно помещают палетку равноотстоящих или случайных точек. В каждой точке снимаются количественные значения ai и bi явлений А и В. К выборкам с карт предъявляются определенные требования. Выборки должны быть достаточно большими (не менее 30 значений), характерными для данного явления, охватывающими всю занимаемую площадь.
Прежде чем приступить к определению тесноты связи, необходимо получить представление о форме связи, для чего строится график, на котором по значениям ai и bi наносятся точки (i – номер точки, изменяющийся от 1 до n). Точки на графике образуют поле корреляции, по виду которого можно судить о форме и тесноте связи. Если разброс точек велик, то это свидетельствует об отсутствии связи между явлениями. Если же поле точек вытягивается в виде полосы, значит, связь существует, и чем уже полоса, тем связь теснее. Если полоса прямая, то связь между явлениями прямолинейная и она может быть оценена с помощью коэффициента корреляции
,
(1)
где
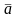и
– средние арифметические величины,
,
;
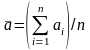(2)
– средние квадратические отклонения,
,
;
(3)
n – число пар данных, полученных с карт.
Когда в расчетах используются выборки с многозначными числами, вычисления становятся достаточно трудоемкими. Существуют два пути упрощения расчетов:
1. Группировка данных в особую таблицу и вычисление r по специальным формулам.
2. Использование упрощенных данных и упрощенных схем вычисления.
Рассмотрим
подробнее второй способ, особенно
удобный, когда
.
В этом случае r можно вычислять по
преобразованной формуле
,
(4)
где
;
.
При использовании упрощенной схемы вычислений все исходные данные, снимаемые с карт, записываются в ведомость (см. пример выполнения задания).
Приближенное значение средней квадратической ошибки коэффициента корреляции подсчитывают по формуле
.
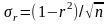(5)