Математическая модель

В проблемную систему включаем следующие объекты и показатели:

1. количество денежных средств инвестора;

2. цели инвестора;

3. ассортимент возможных для покупки рыночных активов с их характеристиками доходности и риска;

4. портфельная теория и ее прикладной инструментарий.

Инвестор заинтересован в большой доходности портфеля. В одноиндексной (однофакторной) модели Шарпа доходность портфеля определяется по формуле:

Rp = Rf + (Rm – Rf) * Bp,

где Rp- доходность портфеля, %; Rf- доходность безрисковых активов, %; Rm- доходность рынка, %; Bp- Бета портфеля- показатель системного, рыночного риска портфеля.

Bp = ,

где Wi- доля актива i в портфеле; Bi- Бета i- й акции; i- номер бумаги в списке портфеля; n- количество бумаг в портфеле.

Риск портфеля определяется дисперсией доходности портфеля:

Vp = Vm * Bp² + * Vi ,

где Vp- дисперсия доходности портфеля; Vm- дисперсия доходности рынка; Vi- дисперсия доходности i-й бумаги.

Исходными данными для расчета характеристик портфеля являются доходность безрисковых активов (Rf), доходность рынка (Rm), дисперсия (риск) доходности рынка (Vm), Бета каждой акции (Bi), остаточная дисперсия каждой акции (Vi).

Задачи оптимизации портфелей

1. Максимизация доходности портфеля при ограниченном риске (дисперсия доходности портфеля):

Rp max ,

Vp <= Vb,

Wi >= 0,

где Vb- заданное инвестором ограничение риска портфеля в долях или процентах.

2. Минимизация риска при заданном ограничении уровня доходности портфеля:

Vp min,

Rp >= Rb,

Wi >= 0,

где Rb- заданное инвестором ограничение по уровню доходности портфеля в долях или процентах.

Табличная модель

В проблемную систему включаем следующие объекты и показатели, показанные в таблице 1.

Таблица 1

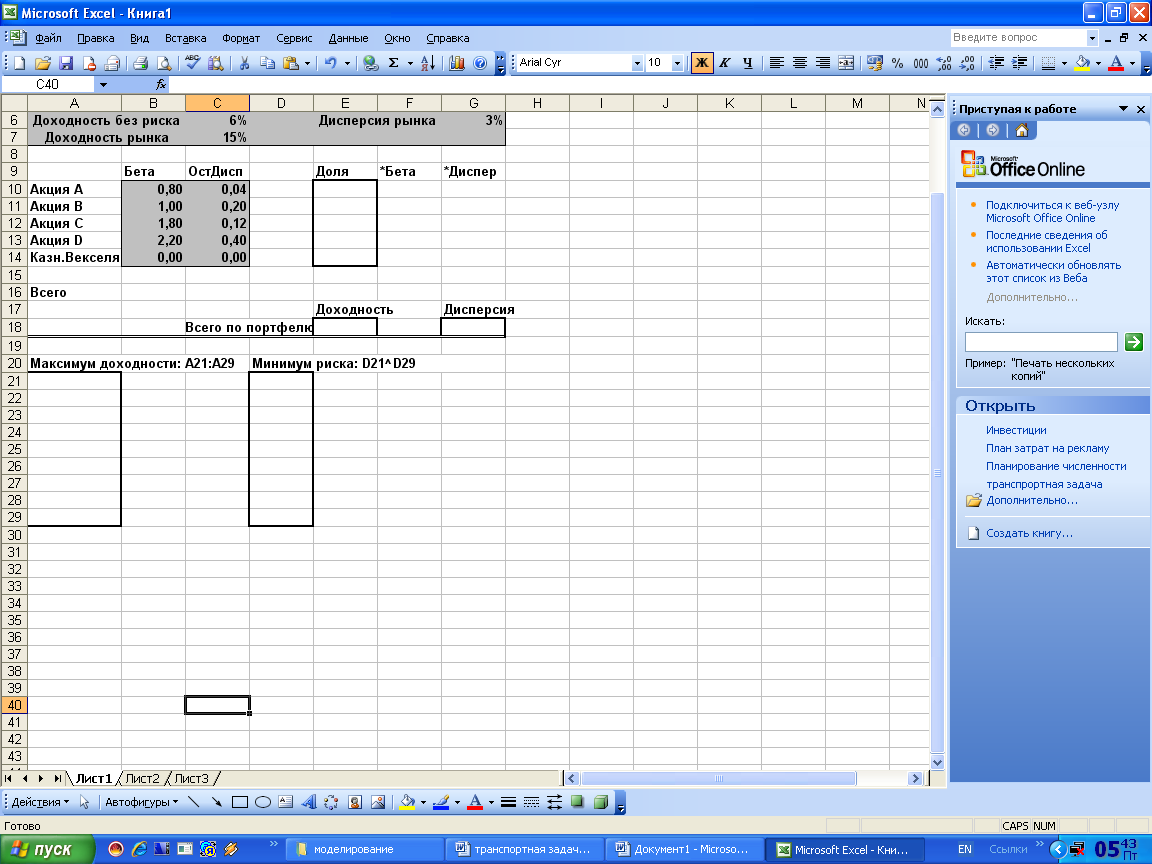
В 6 и 7 строках введены исходные данные по показателям, характеризующим рынок:

• доходность безрисковых активов Rf = 6% (Risk- free rate, безопасная скорость);

• доходность рынка Rm = 15% (Market rate, биржевая скорость);

• дисперсия рынка Vm = 3% (Market variance, биржевые изменения);

В колонке А приведены наименования акций компаний. В колонке В- исходные данные по Бета акций B_i. В колонке С- исходные данные по остаточной дисперсии акций V_i .

В диапазон Доля в колонку Е вручную или программой Поиск решения вводятся процентные доли каждой конкретной ценной бумаги в составе портфеля. Это искомый план портфеля. В ячейке Е16 вычисляется сумма долей бумаг в портфеле. Она должна быть равна 100%.

В колонке F вычисляются портфельные Бета для каждой бумаги с учетом ее доли в портфеле. Это произведение элементов векторов Доля и Бета.

Бета портфеля как скалярное произведение этих векторов суммируется в ячейке F16.

Для дисперсии каждой бумаги в портфеле вычисляется в колонке G как произведение квадрата весов (долей) бумаг в портфеле на исходные данные остаточной дисперсии.

Сумма частных портфельных дисперсий бумаг вычисляется в ячейке G16. Общая портфельная дисперсия вычисляется в ячейке G18. Доходность портфеля- в ячейке Е18. Дисперсия и Доходность являются целевыми (критериальными) ячейками в вариантах задач выбора наилучшего (оптимального) портфеля ценных бумаг.