2.3.2. Правила сложения для д2 кодов.

Рассмотрим таблицу возможных значений выходов для Д2 кода (табл.2). Анализ таблицы показывает, что при сложении чисел в Д2 коде могут возникнуть следующие случаи:

1). <5 , <5 тогда :

а) если <5-коррекция отсутствует

б) если 5 , вводим коррекцию +6₁₀(0110)₂

2). <5 , 5 тогда , коррекция отсутствует .

3). 5 , 5 тогда :

a). Если 21 С_i 26 вводим коррекцию результата -6₁₀(-0110)₂ т.е. +10₁₀(1010)_2..

б).если С_i >26 коррекция отсутствует .

где , , – слагаемые и сумма в Д₂ ;

С_i – сумма в Д1 коде.

(S_i и сумма по модулю два).

Таким образом если возникает запрещенная комбинация то:

а) при отсутствии переноса требуется коррекция +6(0110);

б) при наличии переноса требуется коррекция – 6, что в дополнительном коде будет +10 (1010).

Действительно, если число А_i<5,B_i<5 и С_i=А_i+B_i+P_i-1<5, (здесь А_i = _и B_i = ) , из таблицы (таблица 4) видно что сумма С_i попадает в область разрешенных комбинаций I и результат является истиной суммой в Д2 коде , т.е. = C_i.

Если C_i 5, а именно , 5 C_i 10, то результат попадает в область запрещенных комбинаций для Д2 кода (обл.II ).Для получения правильного значения суммы полученный результат необходимо перевести в область разрешенных комбинаций III , где количественный эквивалент чисел в Д2 коде равен значениям от 5 до 9 (см. таблицу). Для выполнения этого необходимо к результату прибавить число 6 (0110). Тогда на выходе сумматора будем иметь истинную сумму в Д2 коде т.е. = С_i+6.

Если одно из слагаемых меньше 5, а другое больше 5 , то результат С_i попадает в область разрешенных комбинаций и следовательно на выходе будет истинная сумма в Д2 коде т.е. С_i= .

Если оба слагаемых 5 ,то в первом случае результат попадает в область запрещенных комбинаций V.

Например: сложить два числа =5(1011), =6(1100), P_i-1 =0 :

где в скобках дано изображение десятичного разряда (тетрады) в Д2 коде).

Тогда при сложении этих чисел на четырех разрядном двоичном сумматоре получим сумму S_i= 0111 и перенос P_i=1. Видно, что количественный эквивалент числа в двоичном коде (23) больше истиной суммы на шесть (должно быть 17).

Действительно :

= А_i +6, = B_i +6, тогда

= А_i +B_i+P_i-1+6+6= +6.

Следовательно для получения правильной суммы в Д2 коде необходимо от полученного результата отнять 6, т.е.

= -6 (0110).

Во втором случае результат попадает в область разрешенных комбинаций (обл. VI). В этом случае коррекция не требуется , так как переход в область VI уносит еще 6 комбинаций . Поэтому :

= С_i+6+6= А_i +B_i+P_i-1+6+6 .

Из вышесказанного следует, что сумматор Д2 кода так же состоит из двух ступеней четырехразрядных двоичных сумматоров с комбинационной схемой, определяющих область запрещенных комбинаций и формирующих поправки.

Табл.2

	Д1 код			Д2 код			примечания
	P4(16)	Si		Pi(10)
		S4S3S2S1			S14S13S12S11
		8 4 2 1			2 4 2 1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31	0	0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1	0 1 2 3 4 5 6 7 8 9 A B C D E F	0	0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 -- -- -- -- -- -- 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1	0 1 2 3 4 5 6 7 8 9		I II Коррекция +6 III
	1	0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1	0 1 2 3 4 5 6 7 8 9 A B C D E F	1	0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 -- -- -- -- -- -- 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1	0 1 2 3 4 5 6 7 8 9	IV V Коррекция -6 VI

где I, III, IV и VI – области разрешенных комбинаций,

II и V – области запрещенных комбинаций.

На первой ступени четырех разрядного двоичного сумматора (SM1….SM4) получаем промежуточный результат суммы двух чисел А_i, B_i и перенос P_i-1. На второй ступени (SM5….SM8) вводим поправку в случае необходимости и на выходе получаем истинную сумму в Д2 коде.

Поправка формируется следующим образом: из таблицы 4 видно, что функция Y, определяющая области запрещенных комбинаций равна “1” на наборах 5, 6, 7, 8, 9,10, 21, 22, 23, 24,25,26. Используя карты Карно находим минимизированное выражение для функции Y.

P4S4*	Y
10					1		1	1		S3*S2*S1*
11	1	1		1
01	1	1		1
00					1		1	1
	000	001	011	010	110		111	101	100

Тогда для выполнения условий введения поправок используем схему сложения по модулю 2. На один ее вход подаем сигнал Y на второй - сигнал переноса Р₄ .

Если сигнал переноса P₄=0, то на вторую ступень сумматоров с комбинационной схемы введения поправок должно поступать число +6(т.е. 0110). Если P₄=1- то число 10 (1010). Откуда видно, что на первый разряд второй ступени сумматоров (т.е. на SM5) в обоих случаях поступает “0”, а на второй (SM6)-“1”.На третий (SM7)-“1” при Р_i=0 и “0” при Р_i=1, а на четвертый (SM8)-“0” при Р_i=0 и “1” при Р_i=1

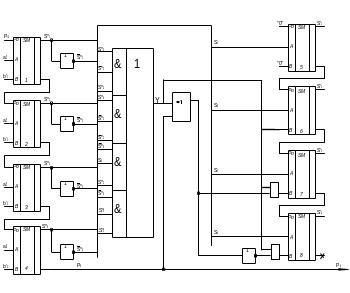
Рис. 2

Схема одного разряда двоично-десятичного сумматора в Д2 коде.