1.4.4. Кривые 2-го порядка
Кривой 2-го порядка называется линия, уравнение которой является уравнением 2-го порядка относительно прямоугольных координат:
Уравнение кривой 2-го порядка определяет окружность, эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, одну точку или же вообще не определяет вещественных точек.
1.4.5. Окружность
Окружностью называется множество всех точек плоскости, находящихся на одинаковом расстоянии, называемом радиусом, от фиксированной точки, называемой центром окружности.
Каноническое
уравнение окружности
здесь R
– радиус окружности, точка
центр
окружности.
Е
сли
центр окружности находится в начале
координат, то уравнение окружности
примет более простой вид:
(см. рисунок).
1.4.6. Эллипс
Эллипсом
называется
множество всех точек плоскости, сумма
расстояний от которых до двух фиксированных
точек, называемых фокусами,
есть величина постоянная. Каноническое
уравнение эллипса, с центром в начале
координат:
здесь
а
> 0 – большая полуось, b
> 0 – малая полуось. Основными параметрами
эллипса являются:
– левый и правый фокусы,
– эксцентриситет,
– левая и правая директриса (см. рисунок).
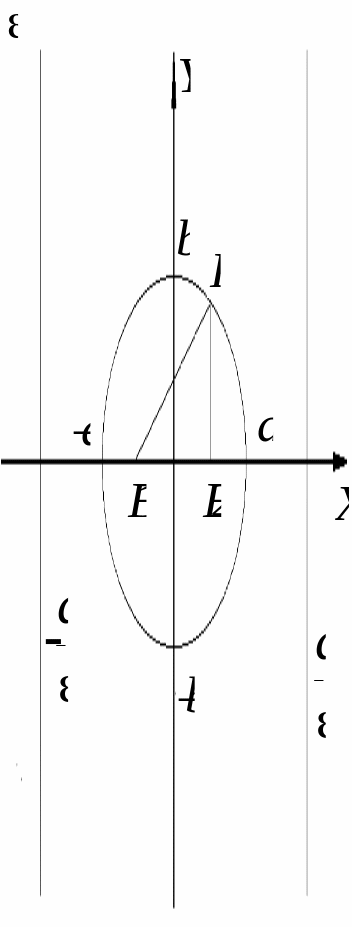
1.4.7. Гипербола
Гиперболой называется множество всех точек плоскости, разность расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.
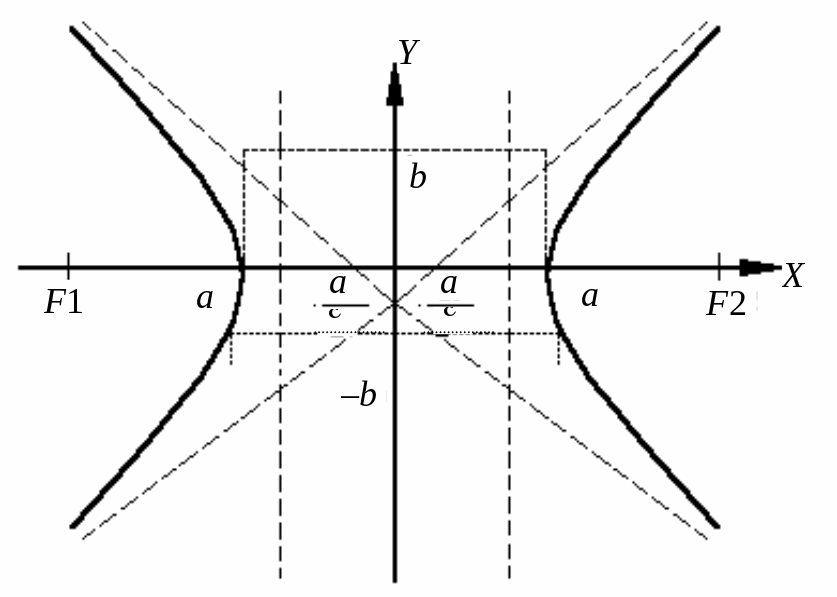
– каноническое
уравнение гиперболы,
– действительная
полуось,
– мнимая
полуось,
–
левый
и правый фокусы,
,
– эксцентриситет,
– левая
и правая директриса,
– асимптоты
гиперболы.
1.4.8. Парабола
П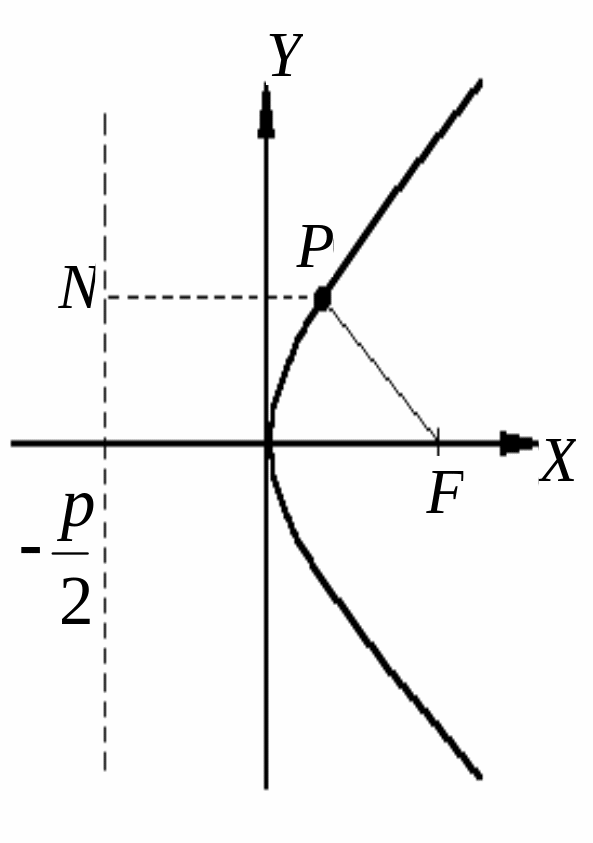
араболой
называется множество всех точек
плоскости, равноудаленных от фиксированной
точки, называемой фокусом
и от данной прямой, называемой директрисой.
– каноническое
уравнение параболы,
– фокальный
параметр,
– фокус,
– директриса.
Пример
Найти уравнение геометрического места точек, отношение расстояний которых от точки F (4; 0) и от прямой х = 25/4 равно 4/5.
Решение.
Возьмем произвольную точку Р
(х,
у),
удовлетворяющую условию задачи. На
прямой
возьмем точку
.
Длина вектора
равна расстоянию от точки Р
до прямой
,
а длина вектора
равна расстоянию от точки Р
до точки
Из
условия задачи находим:
–
эллипс.
Ответ:
– эллипс.
Контрольная работа № 1
Задача № 1. Заданы матрицы А, В, С. Найти: а) (3А + 2В) С; б) det A. Данные, соответствующие вашему варианту, брать в таблице.
Вариант |
А |
В |
С |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
Задача
№ 2. Для
матрицы А найти: а)
; б)
;
в) решить систему
матричным
методом. Данные, соответствующие вашему
варианту, брать в таблице.
Вариант |
А |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
Задача № 3. Решить систему уравнений методом Крамера. Данные, соответствующие вашему варианту, брать в таблице.
Вариант |
Система |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
Задача № 4. Исследовать совместность систем, для совместной системы найти решение. Данные, соответствующие вашему варианту, брать в таблице.
Вариант |
а |
б |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
Задача
№ 5.
Даны вершины пирамиды
,
.
Найти: а) угол между векторами
и
;
б) площадь грани АВС;
в) проекцию вектора
на вектор
;
г) объем пирамиды; д) длину высоты
пирамиды, опущенной из вершины D.
Данные, соответствующие вашему варианту,
брать в таблице.
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
2 |
2 |
–6 |
4 |
–2 |
2 |
4 |
5 |
3 |
6 |
–1 |
2 |
1 |
3 |
2 |
0 |
6 |
2 |
4 |
0 |
0 |
3 |
2 |
7 |
3 |
8 |
4 |
1 |
7 |
7 |
3 |
6 |
5 |
8 |
3 |
5 |
8 |
4 |
7 |
2 |
2 |
5 |
7 |
7 |
5 |
3 |
1 |
2 |
3 |
7 |
5 |
4 |
2 |
5 |
0 |
7 |
1 |
0 |
2 |
7 |
1 |
5 |
0 |
6 |
1 |
–1 |
6 |
4 |
5 |
–2 |
–1 |
3 |
0 |
6 |
1 |
5 |
7 |
3 |
5 |
4 |
8 |
7 |
4 |
5 |
10 |
4 |
4 |
7 |
8 |
8 |
0 |
0 |
2 |
1 |
1 |
0 |
4 |
1 |
2 |
3 |
0 |
5 |
9 |
1 |
–1 |
6 |
4 |
5 |
–2 |
–1 |
3 |
0 |
6 |
1 |
5 |
10 |
1 |
1 |
1 |
3 |
4 |
0 |
–1 |
5 |
6 |
4 |
0 |
5 |
