1.4. Элементы аналитической геометрии

1.4.1. Плоскость в пространстве

Пусть дана ПДСК. Уравнение Аx + By + Cz + D = 0 задает плоскость и называется общим уравнением плоскости. Для написания общего уравнения плоскости надо определить вектор нормали n = Ai + + Bj + Ck (нормаль плоскости – это прямая, перпендикулярная плоскости) и одну точку плоскости

где Если известно общее уравнение плоскости, то можно легко найти нор-мальное уравнение плоскости: ,

где

.

Знак плюс или знак минус выбирается так, чтобы р > 0. Углы – это углы между вектором нормали n и осями координат Ox, Oy, Oz соответственно.

Если известно нормальное уравнение плоскости, то легко найти расстояние от точки до этой плоскости: .

1.4.2. Прямая в пространстве

Прямая, проходящая через точку в направлении вектора s = li + mj + nk, задается:

либо каноническим уравнением прямой ,

либо параметрическим уравнением прямой 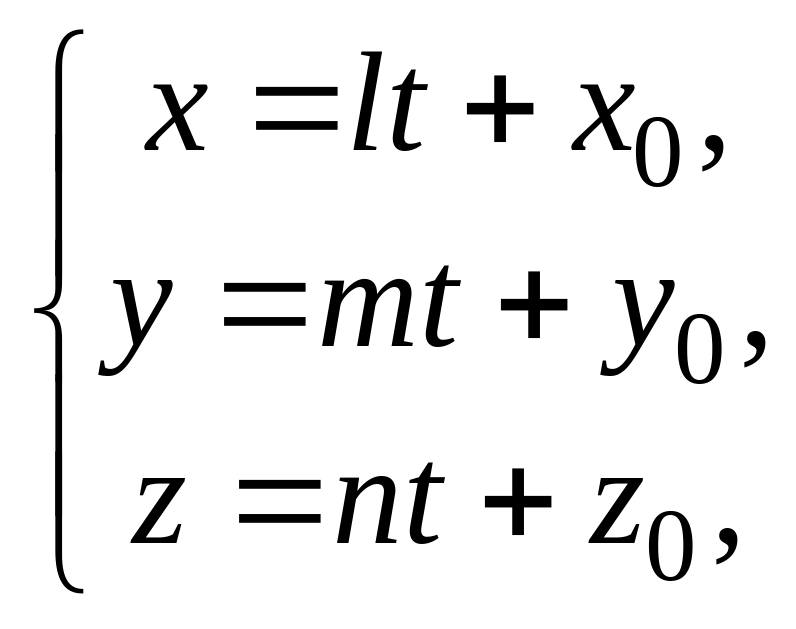где t параметр,

либо прямая задается как пересечение двух плоскостей в этом случае . Вектор s называется направляющим вектором прямой.

1.4.3. Прямая на плоскости

Пусть задана ПДСК на плоскости. Уравнение Ах + Ву + С = 0 задает прямую на плоскости и называется общим уравнением прямой. Для написания общего уравнения прямой надо знать вектор нормали n =Ai + Bj (нормаль прямой – это прямая, перпендикулярная данной прямой) и одну точку прямой :

где

Если известно общее уравнение прямой, то можно найти нормальное уравнение прямой:

где Знак плюс или знак минус выбирается так, чтобы p > 0. Здесь – угол между вектором нормали n и осью Ох.

Если известно нормальное уравнение прямой, то легко найти расстояние  от точки до этой прямой:

Если из общего уравнения прямой выразить переменную y, получим уравнение прямой с угловым коэффициентом у = kx + b, здесь – угловой коэффициент, а – свободный член урав-нения.

Пример 1

В треугольнике с вершинами К (–5; 4), L (1; – 4), М (–9; 1) найти:

а) уравнение прямой, содержащей опущенную из вершины L высоту;

б) длину высоты, опущенной из вершины L;

в) точку N, симметричную точке L, относительно прямой, проходящей через точки К, М.

Решение

а) вектором нормали прямой (Lh), содержащей высоту, является вектор = – 4i – 3j. Находим уравнение прямой

–4(х –1) – 3 (у + 4) = 0, – 4х – 3у – 8 = 0.

(Lh) : 4х + 3у + 8 = 0 – уравнение прямой, содержащей опущенную из вершины L высоту;

б) длина высоты, опущенной из вершины L, равна расстоянию  от точки L до прямой КМ, проходящей через точки К, М. Найдем уравнение этой прямой. Так как = – 4i – 3j, то n = 3i – 4j – век- тор нормали этой прямой. Находим общее уравнение прямой (КМ): 3(х + 5) – 4(у – 4) = 0, КМ : 3х – 4у +31 = 0.

Нормальное уравнение прямой км имеет вид

– – длина высоты.

в) Чтобы найти точку N, необходимо определить точку пересечения прямых Lh, КМ, т.е. необходимо решить систему линейных уравнений

Теперь находим точку Так как то .

Ответ: а) (Lh) : 4х + 3у + 8 = 0, б) , в) N (–11; 12).

Пример 2

Написать каноническое уравнение прямой, проходящей через точку К (3; –7;7) перпендикулярно плоскости, содержащей точки L (–6; 2; –2), M (1; –5; –5), N (2; 3; 1).

Решение. За вектор нормали плоскости LMN, проходящей через точки L, M, N, можно взять вектор, коллинеарный вектору

вектор нор-мали плоскости LMN.

Вектор нормали к плоскости LMN является направляющим вектором прямой S, проходящей через точку К перпендикулярно плоскос- ти LMN:

каноническое уравнение прямой.

Ответ:

Пример 3

Написать общее уравнение плоскости, проходящей через точку L (–3; –2; 9) и прямую

Решение. Заданная прямая проходит через точку М (5; 6; –9) в направлении вектора s = 4i –4j – k. Чтобы найти вектор нормали плоскости, необходимо найти вектор 8i + 8j – 18k, а затем векторное произведение

Следовательно, n =5i + 4j + 4k – вектор нормали плоскости. Тогда

5(х +3) + 4 (у + 2) + 4 (z – 9) = 0, 5 x + 4у + 4z – 13 = 0 – общее урав-нение плоскости.

Ответ: 5х +4у + 4z – 13 = 0.