
- •Оглавление
- •Раздел 1. Элементы линейной и аналитической геометрии 4
- •Элементы линейной алгебры и аналитической геометрии
- •1.1. Элементы линейной алгебры
- •1.1.1. Матрицы. Действия с матрицами
- •1.1.2. Определители 2-го и 3-го порядков
- •Пусть дана система линейных алгебраических уравнений:
- •1.1.5. Ранг матрицы. Решение систем линейных уравнений методом Гаусса
- •Рассмотрим систему линейных алгебраических уравнений
- •1.2. Векторы
- •1.2.1. Понятие геометрического вектора
- •1.2.2. Модуль вектора
- •1.2.8. Скалярное произведение векторов и его свойства
- •1.2.9. Векторное произведение векторов и его свойства
- •1.3.2. Нахождение координат вектора, заданного двумя точками
- •1.3.3. Линейные операции над векторами
- •1.3.4. Произведения векторов в пдск
- •1.4. Элементы аналитической геометрии
- •1.4.1. Плоскость в пространстве
- •1.4.2. Прямая в пространстве
- •1.4.3. Прямая на плоскости
- •Нормальное уравнение прямой км имеет вид
- •1.4.4. Кривые 2-го порядка
- •1.4.5. Окружность
- •1.4.6. Эллипс
- •1.4.7. Гипербола
- •1.4.8. Парабола
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Список литературы
1.2.9. Векторное произведение векторов и его свойства
Вектор с, удовлетворяющий условиям:

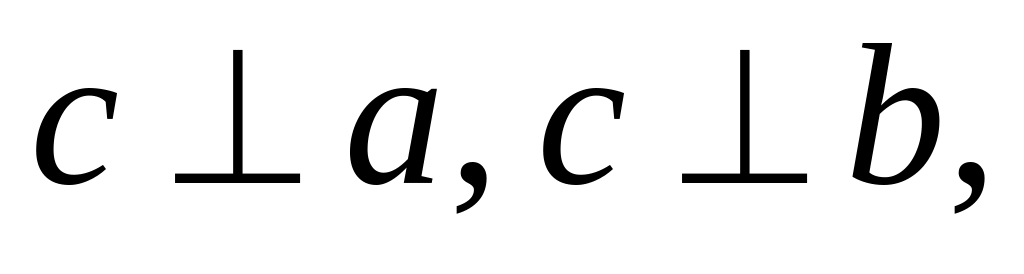
векторы a, b, c образуют правую тройку векторов;
называется
векторным
произведением векторов
и обозначается
![]()
Векторное произведение обладает свойствами:


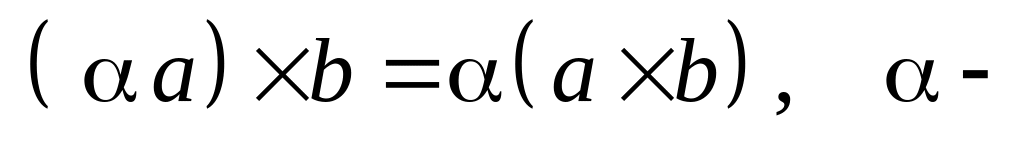 вещественное
число;
вещественное
число;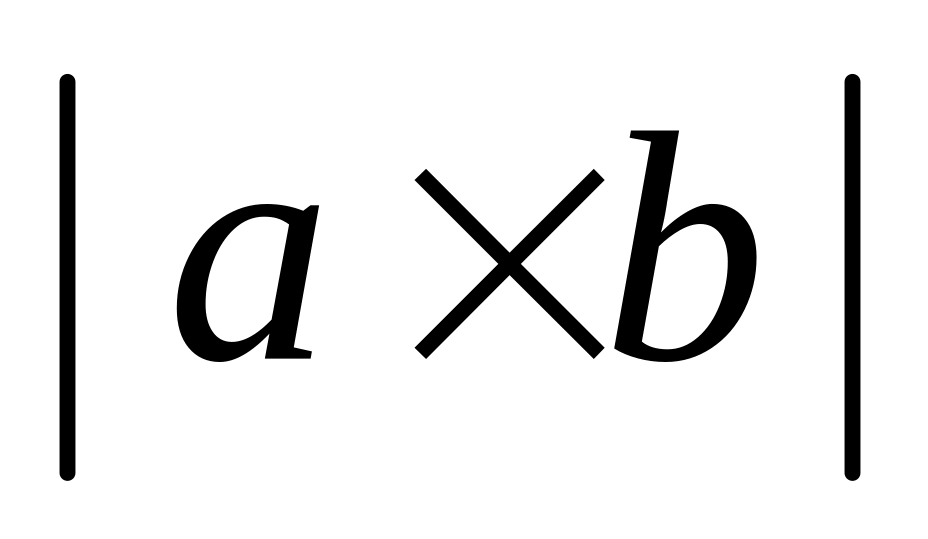 равен
площади параллелограмма, построенного
на векторах a,
b;
равен
площади параллелограмма, построенного
на векторах a,
b;если
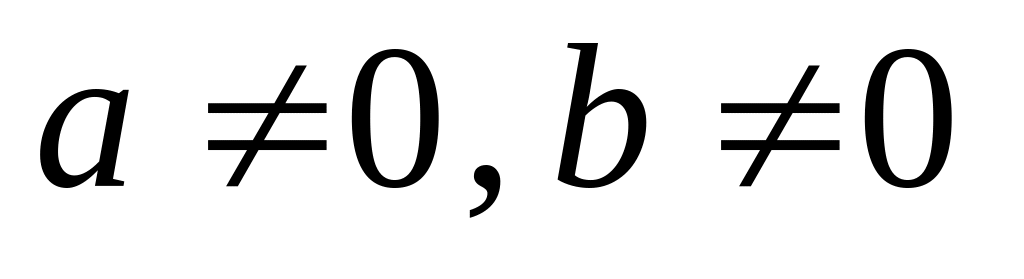 и
и
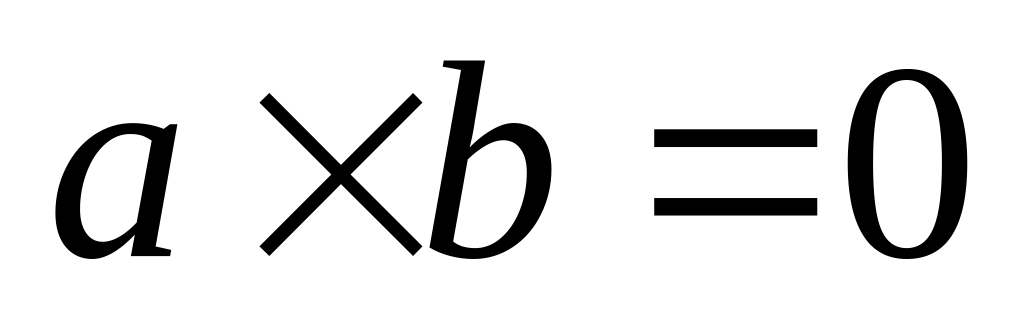 ,
то
,
то
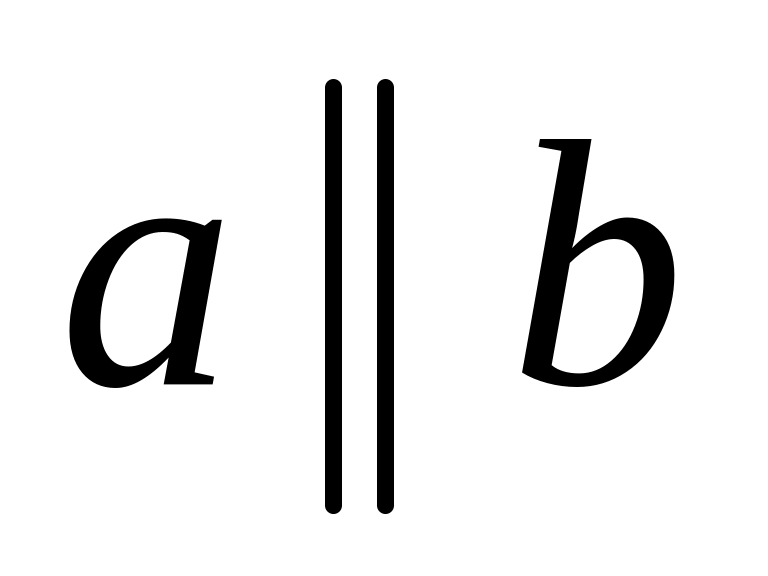 .
.
Смешанное произведение векторов
и его свойства
Число
![]() называется смешанным
произведением векторов а,
b,
c
и обозначается (а,
b,
с).
называется смешанным
произведением векторов а,
b,
c
и обозначается (а,
b,
с).
Если a, b, c – компланарные векторы, то (a, b, c) = 0. Модуль смешанного произведения некомпланарных векторов равен объему параллелепипеда, построенного на этих векторах.
Смешанное
произведение трех векторов
![]()
![]()
![]() определяется формулой
определяется формулой
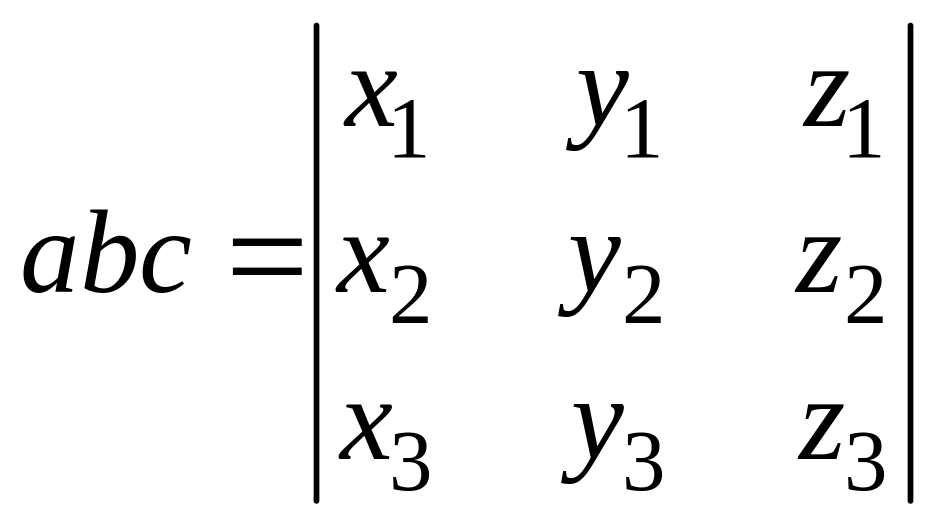 .
.
1.3. Прямоугольная декартова система
координат (ПДСК)
1.3.1. Определение прямоугольной декартовой
системы координат
П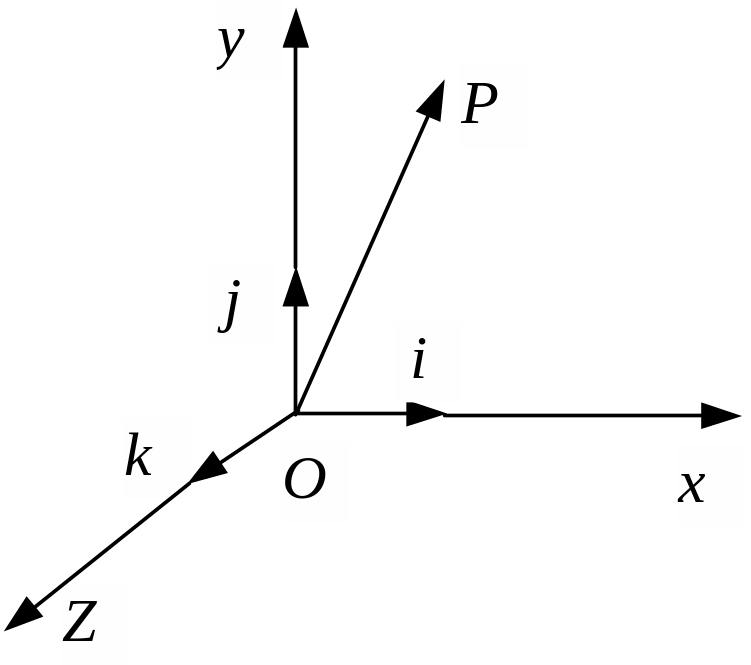 рямоугольная
декартова система координат (ПДСК)
состоит из фиксированной точки О
(центра системы координат) и трех
пересекающихся в ней, взаимно
перпендику-лярных прямых Ox,
Оу,
Оz
(осей системы координат). Направления
выбираются так, чтобы прямые образовывали
правую трой-ку векторов.
рямоугольная
декартова система координат (ПДСК)
состоит из фиксированной точки О
(центра системы координат) и трех
пересекающихся в ней, взаимно
перпендику-лярных прямых Ox,
Оу,
Оz
(осей системы координат). Направления
выбираются так, чтобы прямые образовывали
правую трой-ку векторов.
Единичные векторы, задающие направления осям Ox, Oу, Oz, обозначаются буквами i, j, k и образуют ортонормированный базис.
Вектор
![]() называется
радиус-вектором точки Р.
Координаты
вектора
относительно базиса i,
j,
k
являются координатами точки Р,
т.е., если
называется
радиус-вектором точки Р.
Координаты
вектора
относительно базиса i,
j,
k
являются координатами точки Р,
т.е., если
![]()
![]() ,
то
,
то
![]() –
точка с координатами
–
точка с координатами
![]()
Т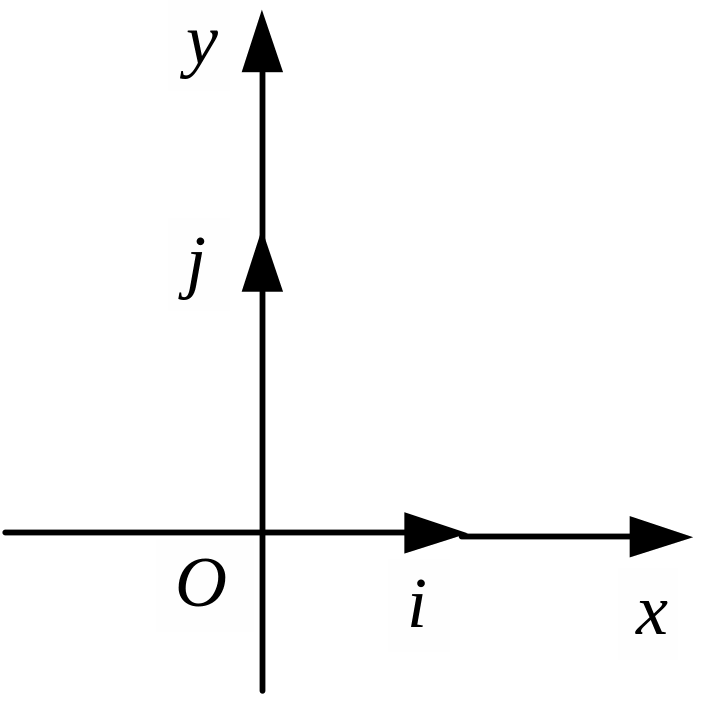 ак
как
i
= i, j = j, k = k
, то
i
= {1;
0; 0},
j
= {0;1;0}, k
=
{0;0;1}.
ак
как
i
= i, j = j, k = k
, то
i
= {1;
0; 0},
j
= {0;1;0}, k
=
{0;0;1}.
Если векторы рассматриваются на плоскости, то ПДСК состоит из двух перпендикулярных осей Ох, Оу с направляющими ортами i, j(i = {1; 0}, j = {0; 1} ).
1.3.2. Нахождение координат вектора, заданного двумя точками
Пусть
в ПДСК заданы точки
![]() .
Тогда
.
Тогда
![]() ,
т.е. чтобы найти координаты вектора,
необходимо из координат конца вектора
отнять координаты начала вектора.
,
т.е. чтобы найти координаты вектора,
необходимо из координат конца вектора
отнять координаты начала вектора.
1.3.3. Линейные операции над векторами
Пусть
в ПДСК заданы векторы
![]() .
Тогда
.
Тогда
![]()
![]() вещественное
число.
вещественное
число.
Векторы
![]() и
и
![]() являются коллинеарными, если
являются коллинеарными, если
![]() ,
их направления совпадают, если
,
их направления совпадают, если
![]() ,
их направления противоположны.
,
их направления противоположны.
1.3.4. Произведения векторов в пдск
Пусть
в ПДСК заданы векторы
![]()
![]() .
Тогда
.
Тогда
![]() – скалярное про-
изведение,
– скалярное про-
изведение,
![]() =
=
![]() –
модуль
вектора,
–
модуль
вектора,
 – векторное произведение,
– векторное произведение,
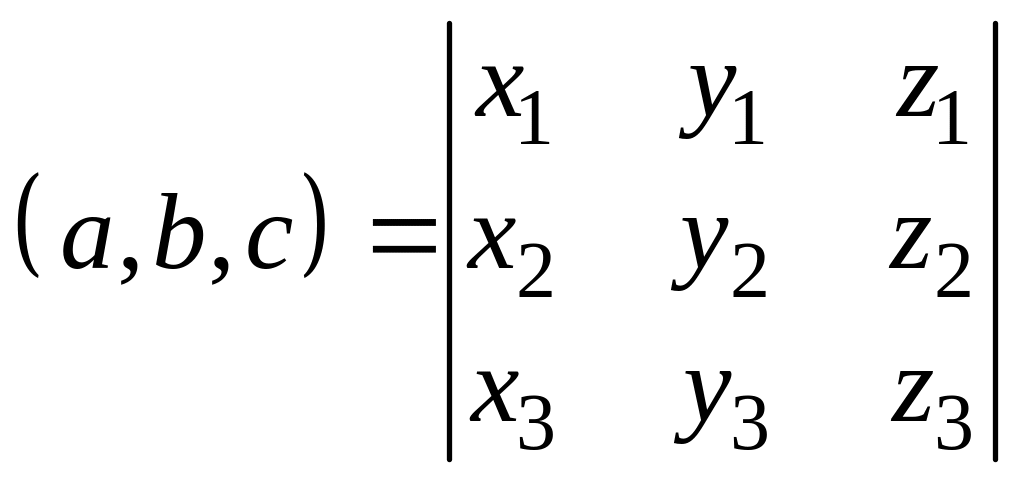 – смешанное произведение.
– смешанное произведение.
Пример 1
В
ПДСК даны векторы
![]() Найти единичный вектор х,
перпендикулярный векторам а,
b.
Найти единичный вектор х,
перпендикулярный векторам а,
b.
Решение.
Вектор с = а
![]() b
перпендикулярен векторам а,
b.
b
перпендикулярен векторам а,
b.
c
= a
b
=

![]()
![]() В
качестве вектора х
можно взять
В
качестве вектора х
можно взять
вектор
х
=
![]() или вектор х
=
или вектор х
=
![]()
Векторы
a,
b,
![]() образуют
правую
тройку векторов,
а a,
b,
образуют
правую
тройку векторов,
а a,
b,
![]() левую.
левую.
Ответ:
х
![]() или
х
или
х
![]()
Пример 2
Найти
![]() х
если известно,
что х = а + 2b,
у= 2а
– b,
х
если известно,
что х = а + 2b,
у= 2а
– b,
![]() угол
между векторами а,
b
равен
угол
между векторами а,
b
равен
![]()
Решение.
![]() Используя свойства скалярного
произведения, находим
Используя свойства скалярного
произведения, находим
(х, у) = (а + 2b, 2a – b) = 2(a, a) + 3(a, b) – 2(b, b) =
=![]()
![]() =
(2a
– b, 2a
– b) = 4(a,
a) – 4(a,
b) + (b, b) =
=
(2a
– b, 2a
– b) = 4(a,
a) – 4(a,
b) + (b, b) =
=
![]()
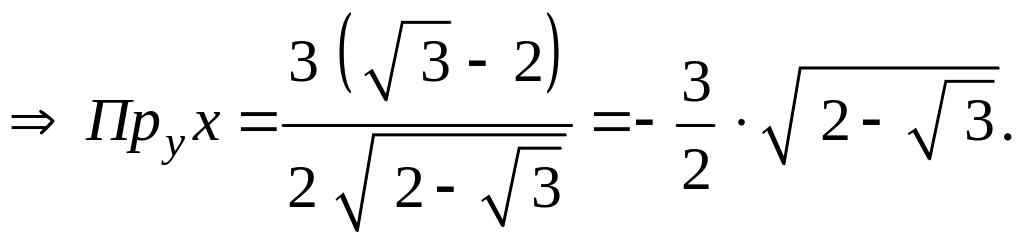
Ответ:
![]()
Пример 3
В ПДСК заданы векторы a = i + 3j – k, b = -i – j + k, c = 2i – j + 3k. Найти вектор х такой, чтобы его скалярное произведение с векторами a, b, c равнялось –12, 6, –8 соответственно.
Решение.
Пусть х =
![]() i
+
j
+
i
+
j
+![]() k.
Из условия задачи получаем
k.
Из условия задачи получаем
(а,
х) =
![]()
(b,
x)
= –![]()
(с,
х) =
![]()
Необходимо
решить систему линейных алгебраических
уравнений с неизвестными
![]() По формуле Крамера находим
По формуле Крамера находим
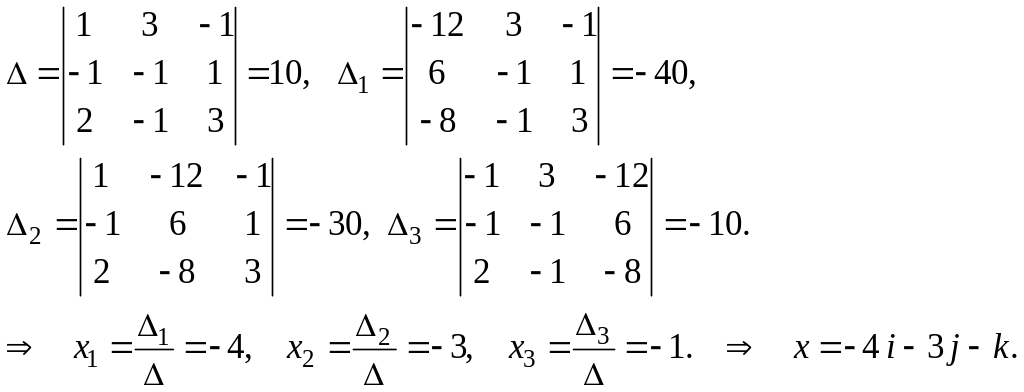
Ответ: x = -4i – 3j – k.
Пример 4
В
ПДСК заданы векторы а
= 2i
– j
+ k,
b
= -3i
+ j
– 2k.
Найти площадь
параллелограмма, построенного на
векторах x,
у, где вектор
х
перпендикулярен векторам а,
b
и
![]() ,
а вектор у =
а + b.
,
а вектор у =
а + b.
Решение. Вектор с = а b перпендикулярен векторам а, b.
с
= а
b
=
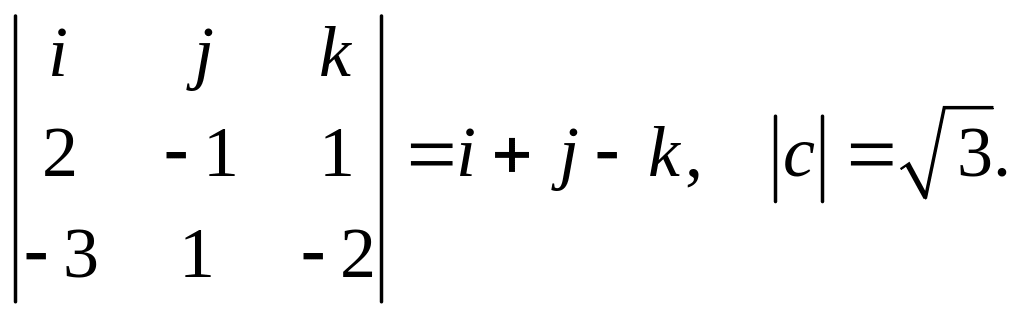
Вектор
х должен
быть коллинеарен вектору с,
так как по условию задачи
![]() то
то
![]() Находим y
= a
+ b
= - i
– k,
Находим y
= a
+ b
= - i
– k,
x
у =
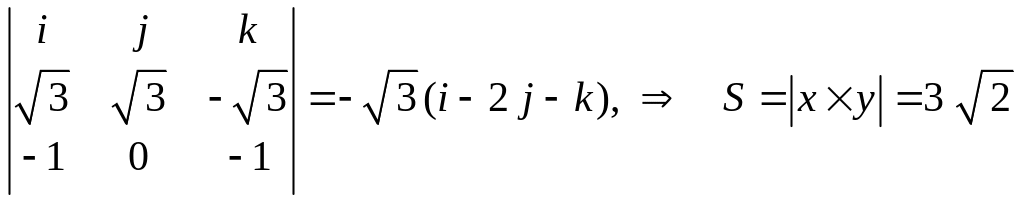 – пло-щадь параллелограмма, построенного
на векторах х,
у.
– пло-щадь параллелограмма, построенного
на векторах х,
у.
Ответ:
![]()
Пример 5
В
ПДСК заданы векторы a
= i
–2j
+ k,
b
= i
– j
+ 3k,
и точки М
(1;-3; 5), N
(–2; 1; 4). Найти объем параллелепипеда,
построенного на векторах х,
у, z,
где х = а
b,
y
= 2a
– b,
z
=![]() .
.
Решение
х
= а
b
=
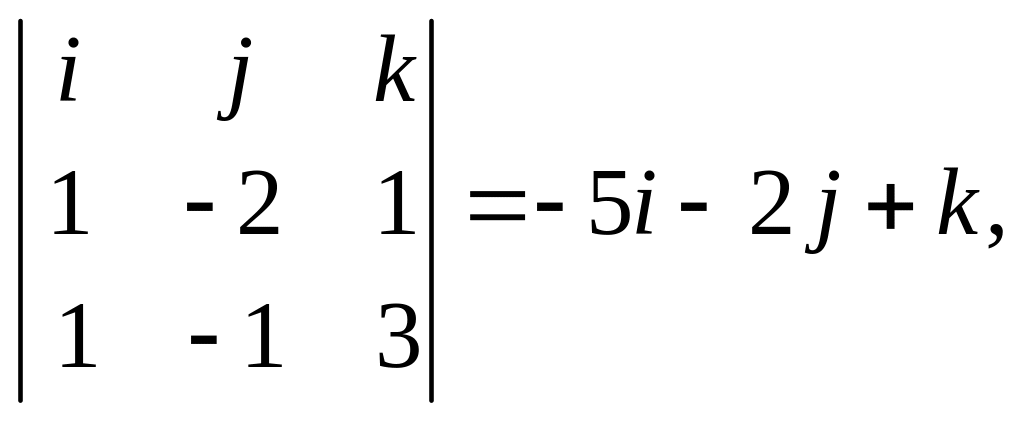 y
= 2a
– b
= i
– 3j
– k,
z
=
y
= 2a
– b
= i
– 3j
– k,
z
=
= = -3i + 4j – k.
(x,
y,
z)
=
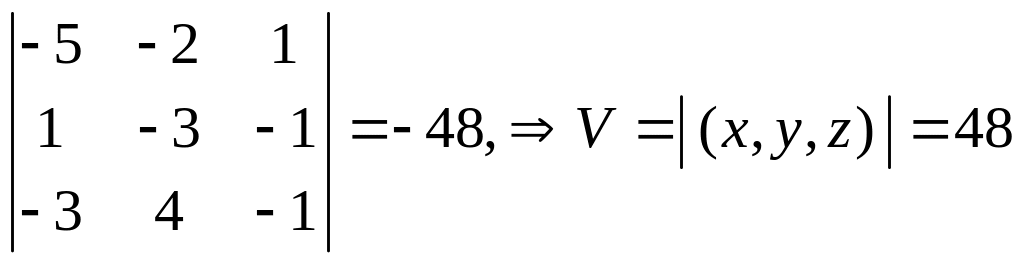 –
объем
параллелепипеда, построенного на
векторах x,
y,
z.
–
объем
параллелепипеда, построенного на
векторах x,
y,
z.
Ответ: V = 48.
