Пусть дана система линейных алгебраических уравнений:

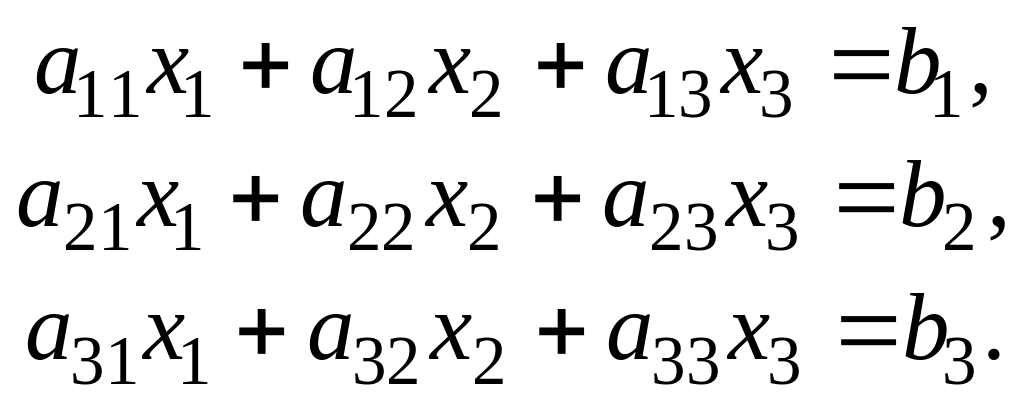
Здесь – постоянные, – неизвестные.

Система имеет единственное решение, если определитель системы не равен нулю:

.

Это решение может быть найдено по формуле Крамера:

где

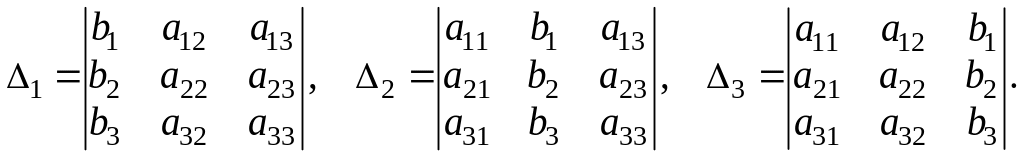
1.1.4. Обратная матрица.

Матричный метод решения систем

линейных алгебраических уравнений

Матрица называется обратной по отношению к квадратной матрице А, если где 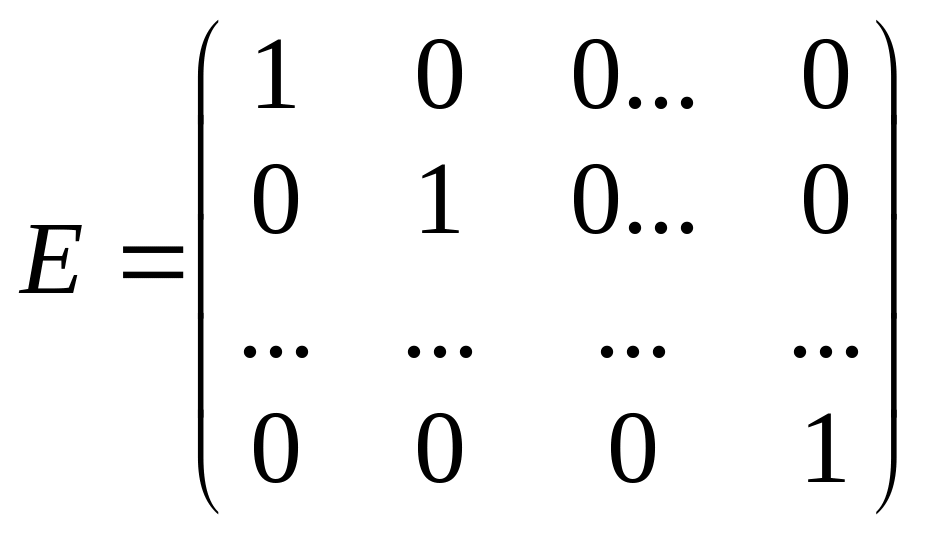– единичная матрица.

Обратная матрица существует для всякой квадратной матрицы, определитель которой отличен от нуля, 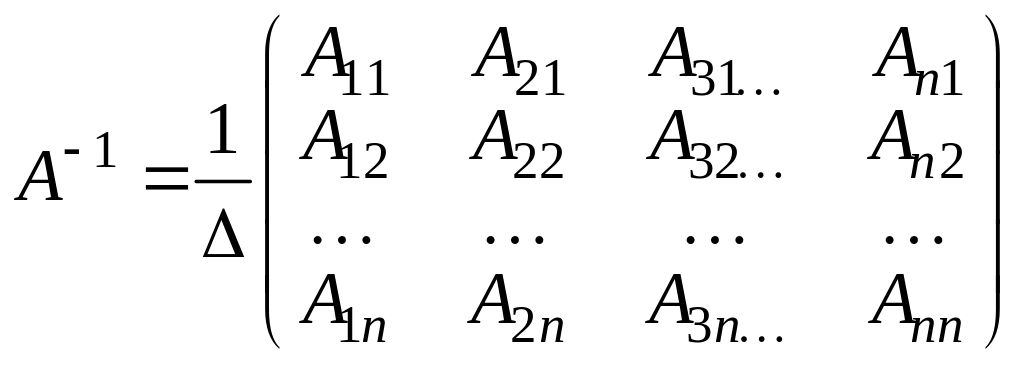, где – определитель матрицы А, – алгебраические дополнения соответствующих элементов матрицы А. Алгебраические дополнения находятся по формуле:

где – определитель, полученный вычеркиванием в определителе матрицы A i-й строки и j-го столбца, называемый минором.

Пусть дана система линейных алгебраических уравнений:

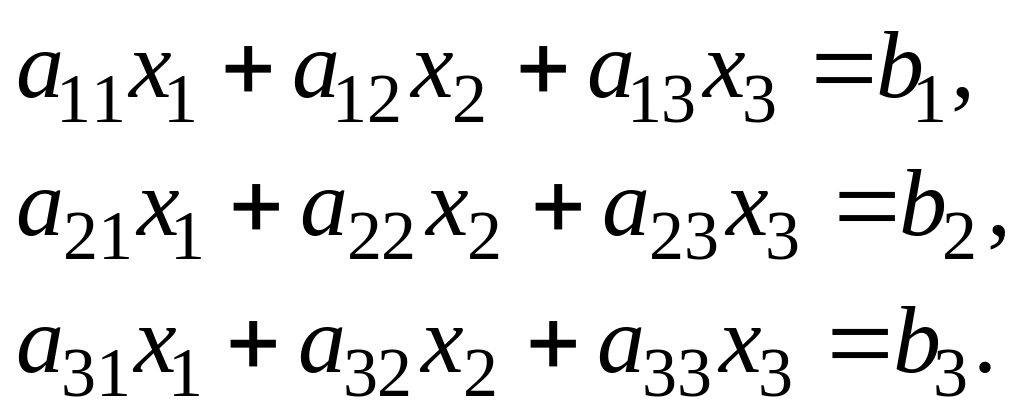Матрица 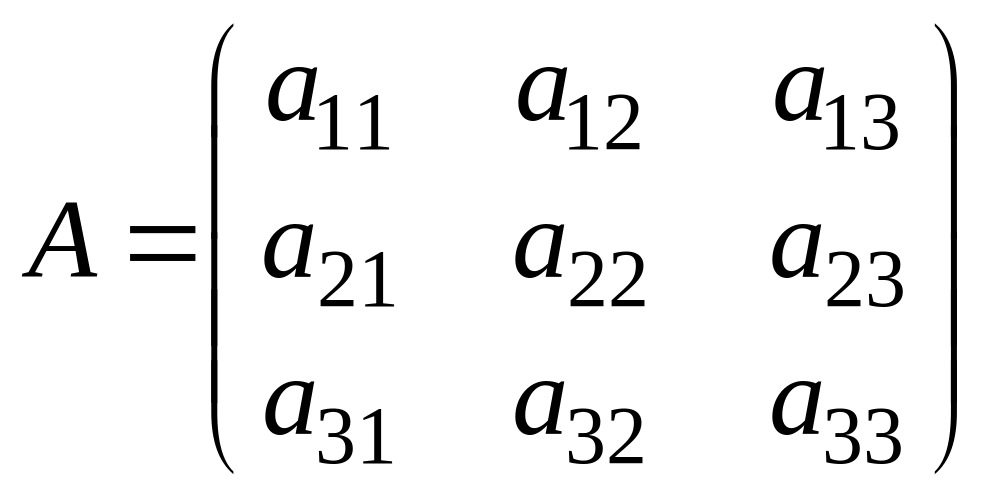называется основной матрицей системы.

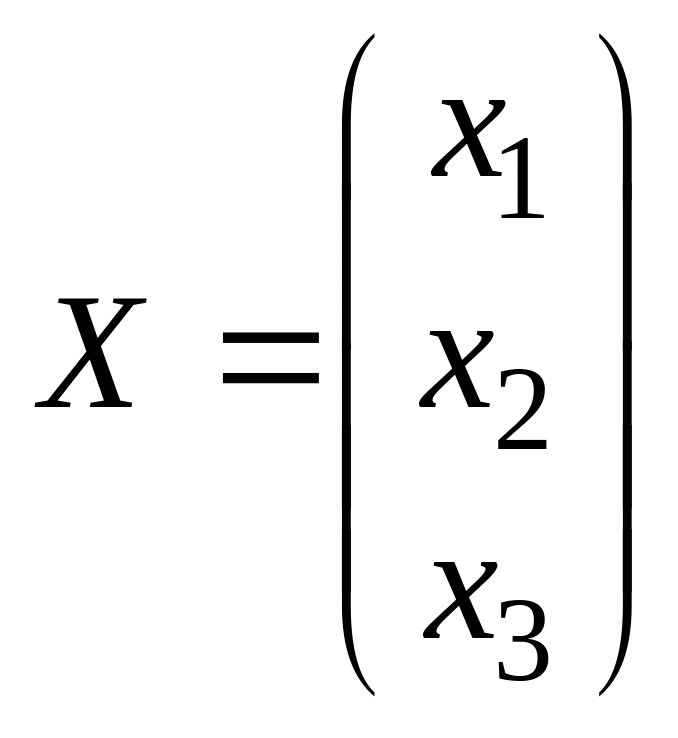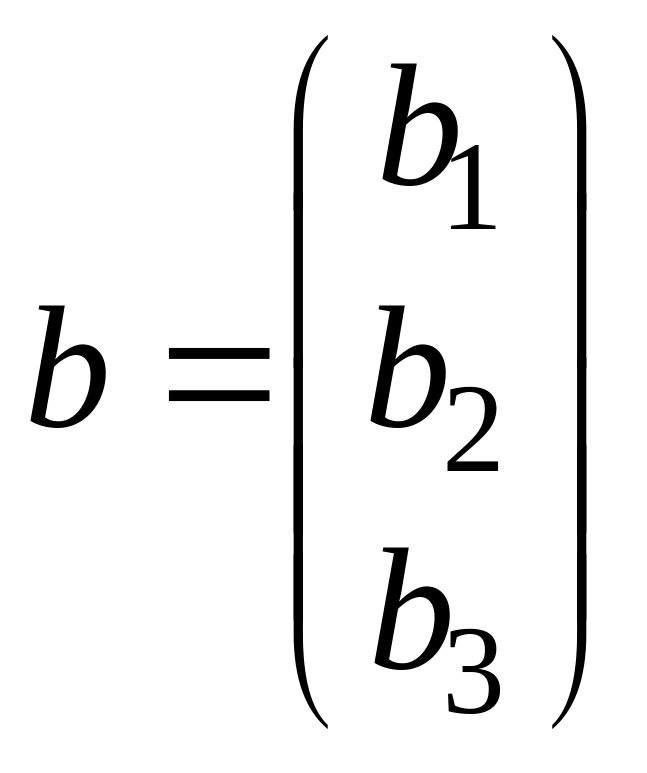Вектор – матрица называется матрицей неизвестных. Вектор – матрица называется матрицей правых частей. Тогда исходную систему можно переписать в виде АХ = b. Решение этой системы находится по формуле Х = А^-1 b.

Пример

Решить систему уравнений матричным методом:

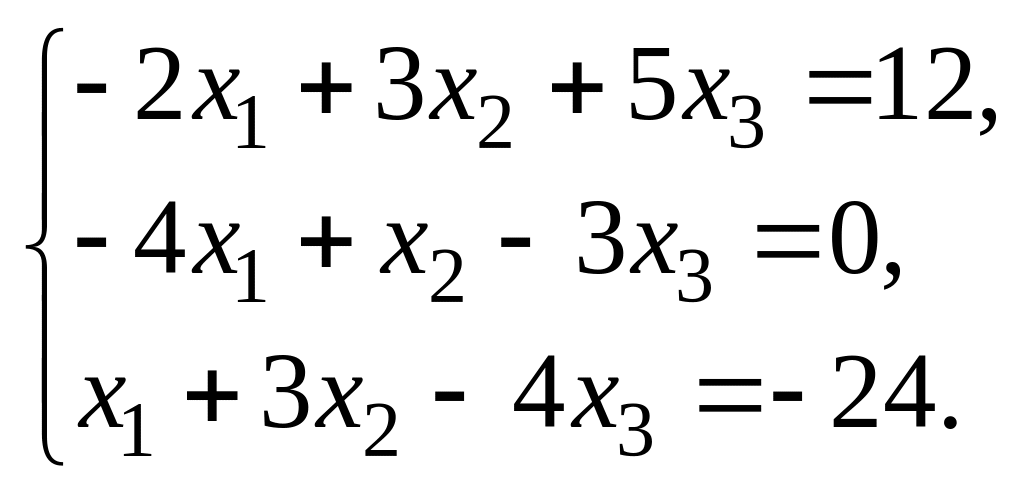
Решение. Найдем определитель основной матрицы системы

Так как определитель отличен от нуля, существует обратная матри- ца А^–1. Для нахождения обратной матрицы находим все алгебраические дополнения:

Тогда

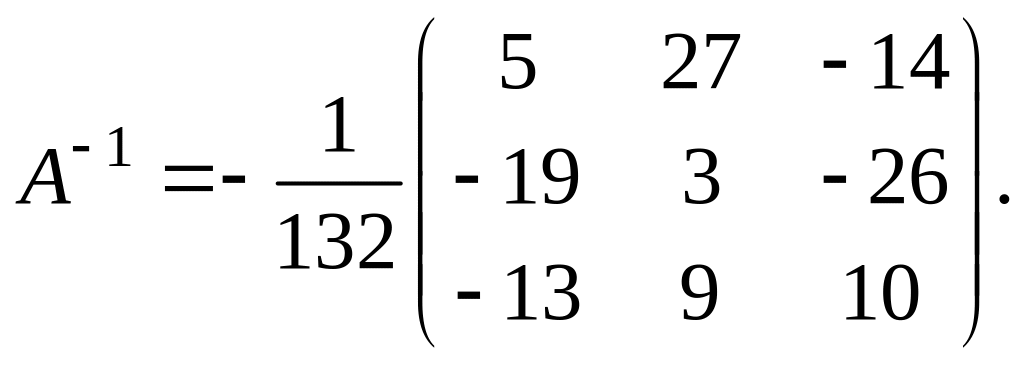
Решение системы где

.

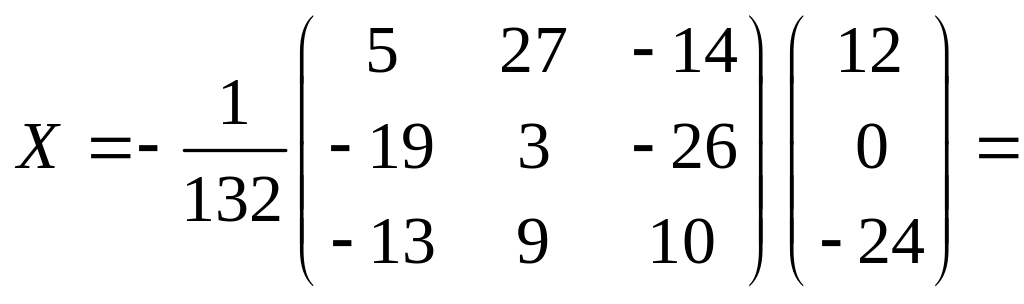
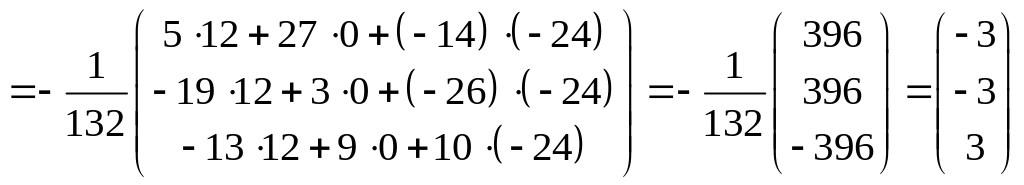Ответ:

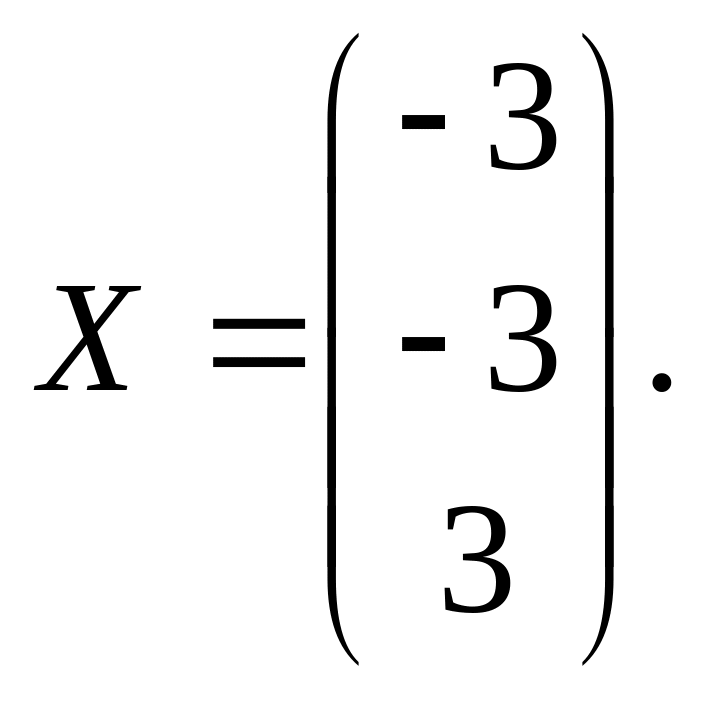
1.1.5. Ранг матрицы. Решение систем линейных уравнений методом Гаусса

Пусть задана произвольная матрица , с помощью цепочки элементарных преобразований приведем матрицу А к «треугольному» виду, получим матрицу 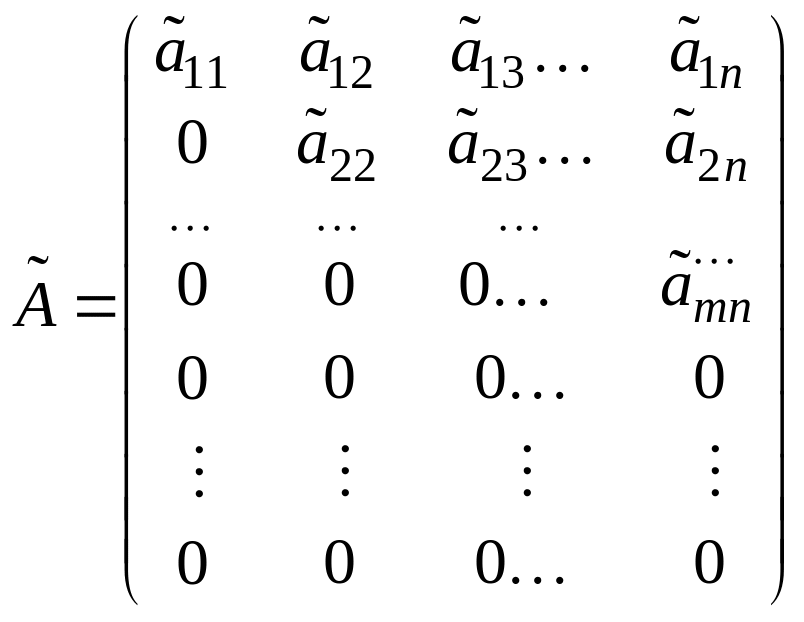. Число ненулевых строк в матрице называется рангом матрицы A и обозначается rangA.

Рассмотрим систему линейных алгебраических уравнений

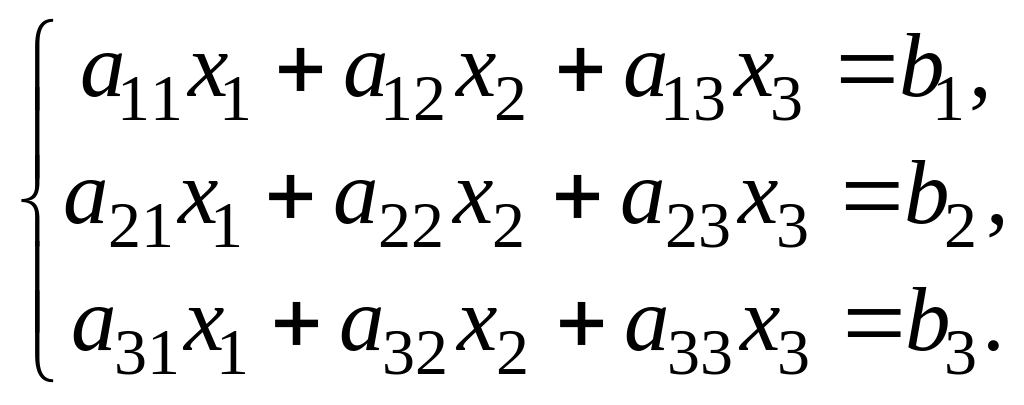Назовем матрицу

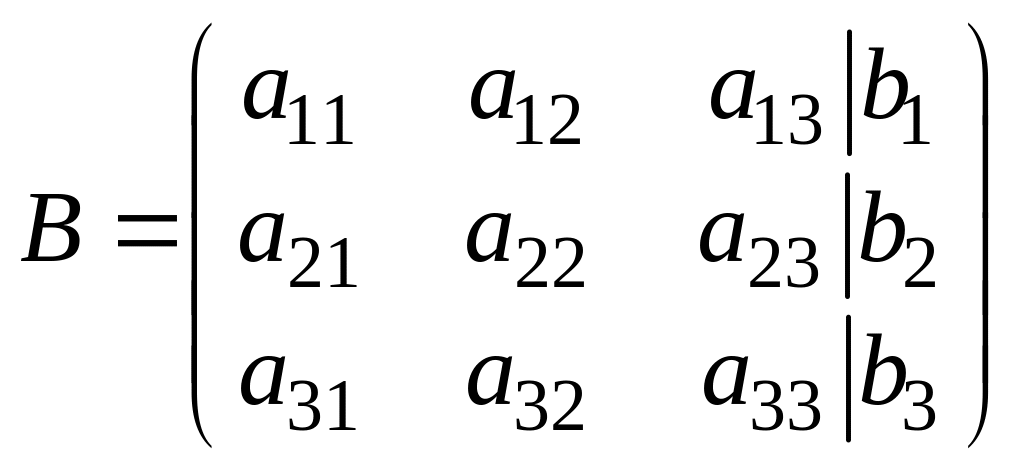
расширенной матрицей системы, которая получается добавлением к матрице А столбца свободных членов . Найдем и , где А – основная матрица системы.

Если: 1) , где n – число неизвестных в системе, то система имеет одно решение;

2) , система имеет бесконечное множество решений;

3) система не имеет решений.

В тех случаях, когда система имеет одно или множество решений, по «треугольному» виду расширенной матрицы восстанавливаем систему и решаем ее снизу вверх.

Пример

Исследовать совместность систем:

а) 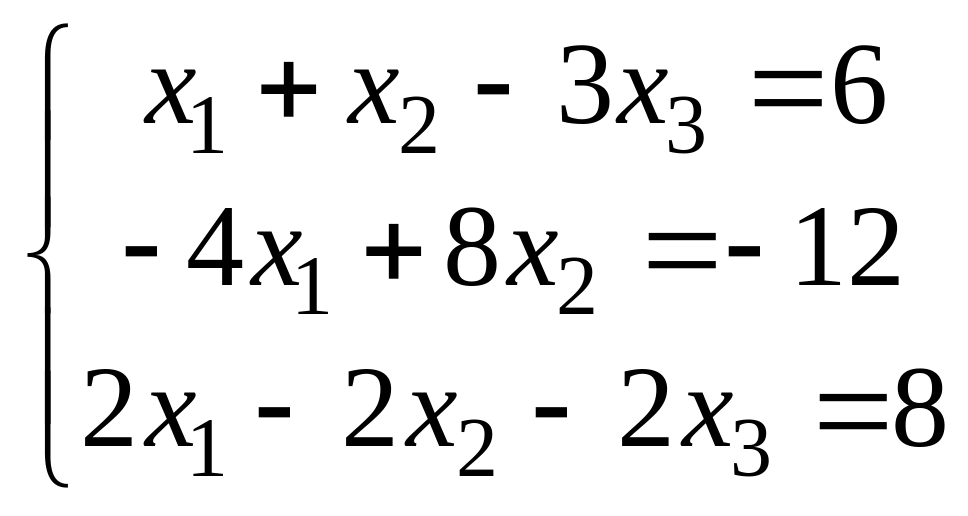; б) Решить совместную систему.

Решение

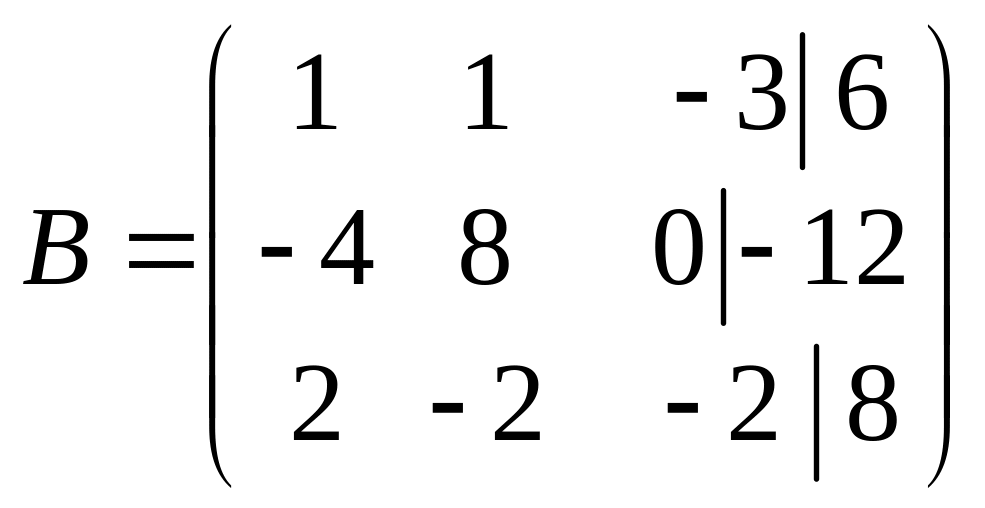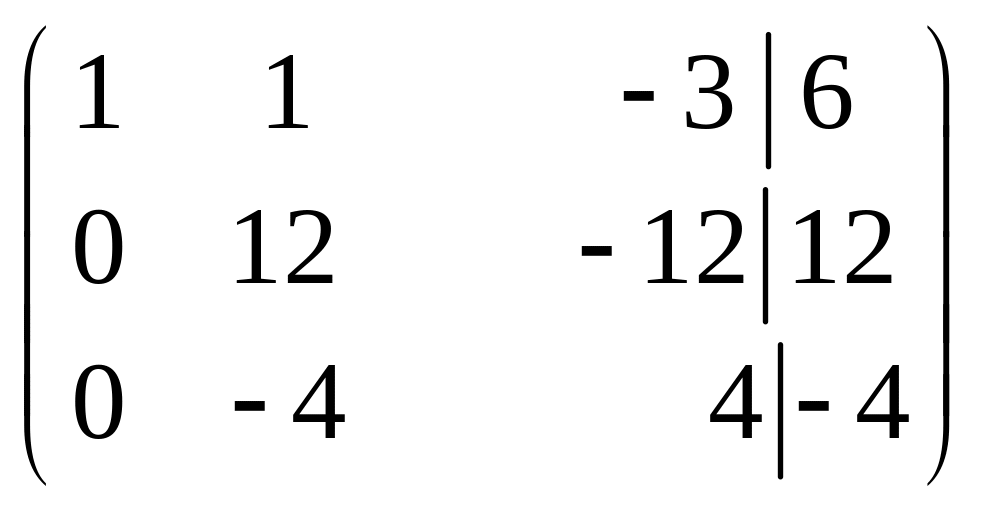а) Запишем расширенную матрицу системы и с помощью цепочки элементарных преобразований приведем ее к «треугольному» виду. ~ (умножим первую строку на 4 и сложим со второй строкой. Затем умножим первую строку на (–2) и сложим с третьей) ~ ~ (поменяем местами вторую и третью строки матрицы) ~ 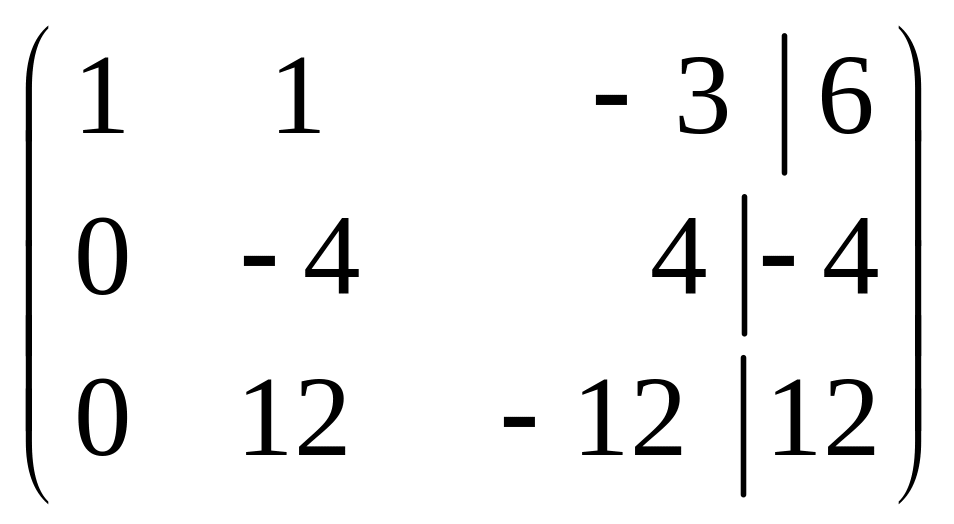~ (умножим вторую строку на 3 и сложим с третьей) ~ . Получим матрицу

в «треугольном» виде. Найдем ранги основной и расширенной матрицы. В «треугольном» виде расширенной матрицы две ненулевых строки, следовательно, rangB = 2. «Треугольный» вид основной матрицы

получаем из «треугольного» вида расширенной матрицы отбрасыванием

последнего столбца, стоящего за чертой 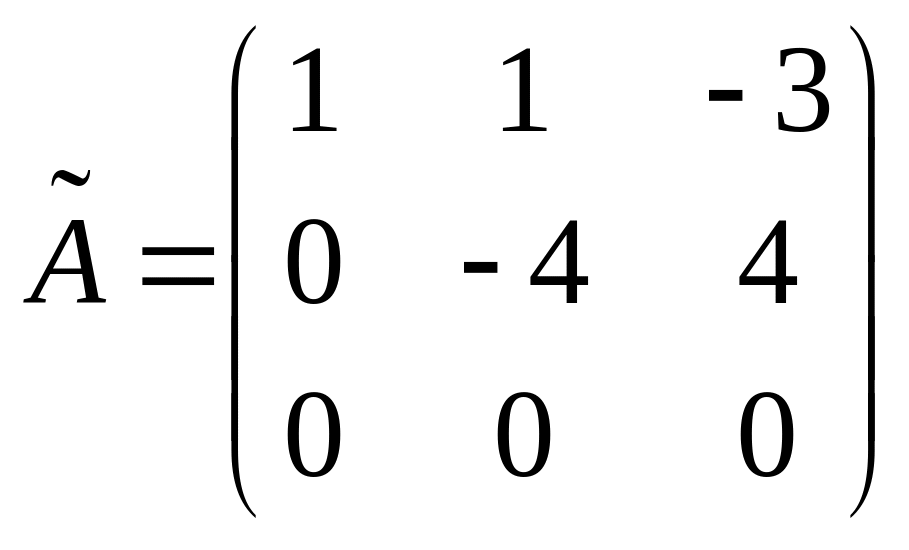, здесь также две ненулевые строки – rangA = 2.

Так как rangA = rangB = 2 < 3, система имеет бесконечное множество решений. Найдем их, для чего восстановим систему по «треуголь-ному» виду расширенной матрицы. из последне- го уравнения найдем и подставим в первое уравнение

.

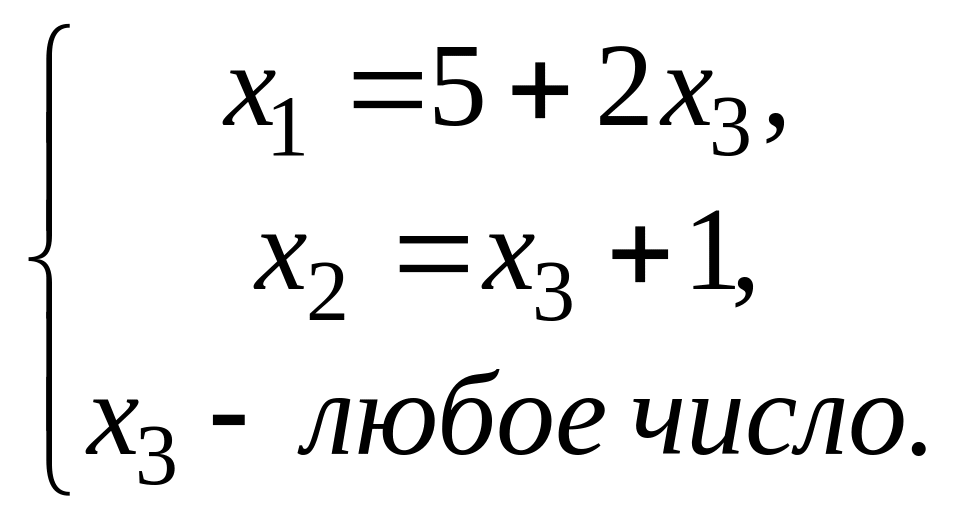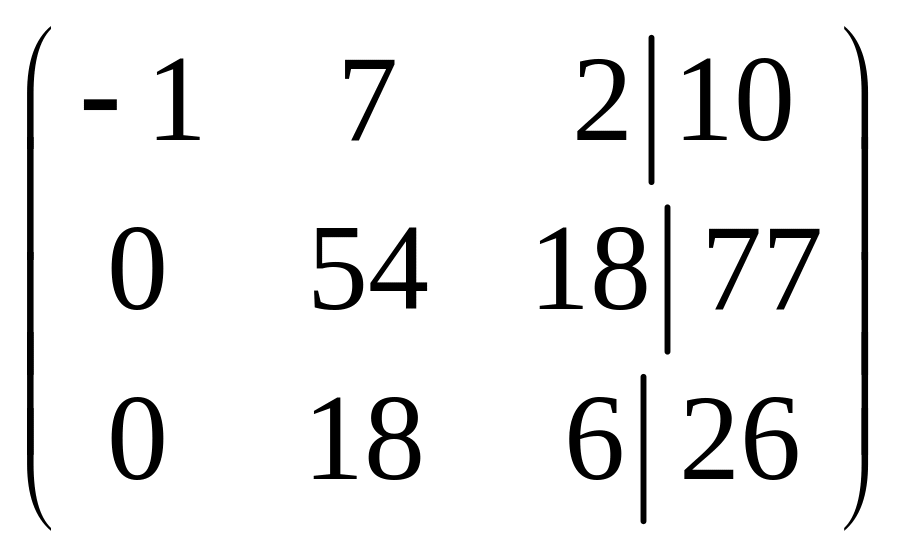б) Запишем расширенную матрицу системы и с помощью цепочки элементарных преобразований приведем ее к «треугольному» виду. ~ (умножим первую строку на 7 и сложим со второй, затем на 2 и сложим с третьей) ~ ~ (поменяем местами вторую и третью строки) ~ 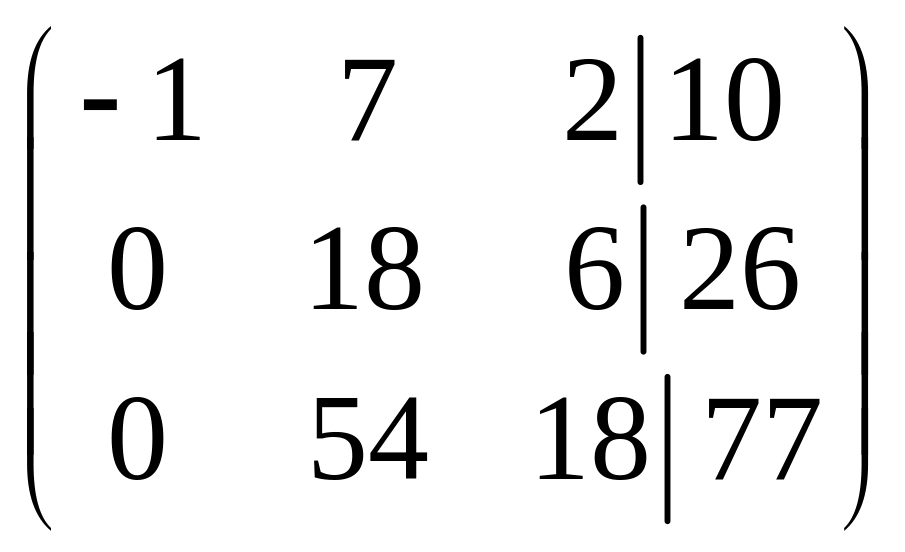~ (умножим вторую строку на (–3) и сложим с третьей) ~ 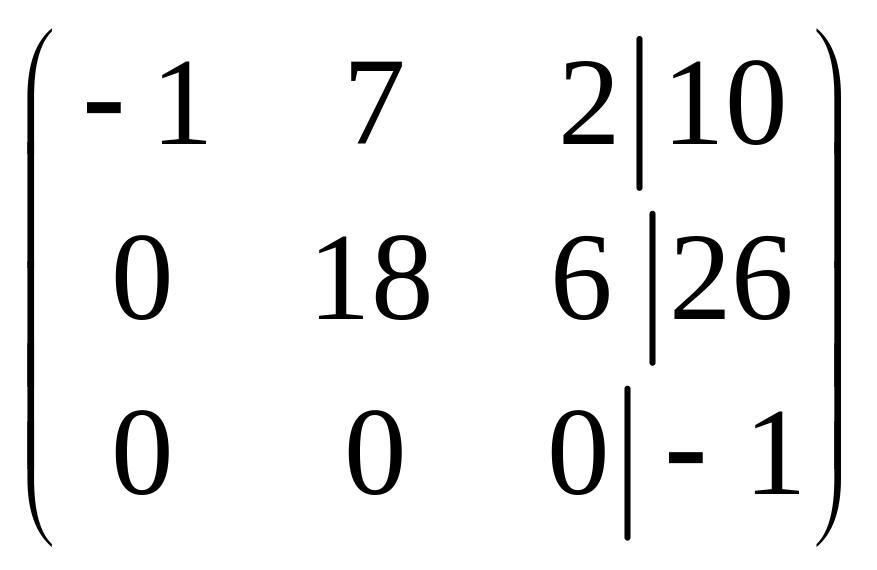. Найдем ранги основной и расширенной матрицы. В «треугольном» виде расширенной матрицы три ненулевых строки, следовательно, rangВ = 3. «Треугольный» вид основной матрицы получаем из «треугольного» вида расширенной матрицы отбрасыванием последнего столбца, стоящего за чертой, 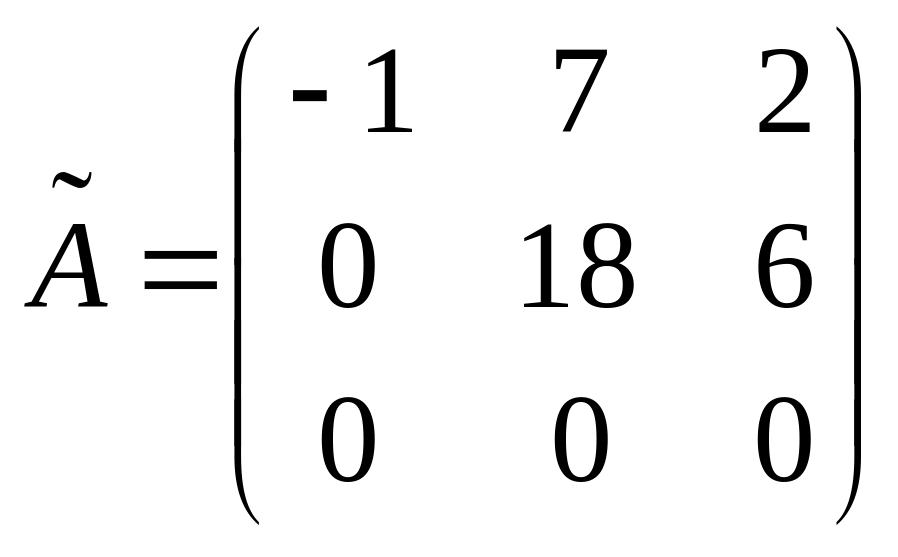, здесь две ненулевые строки – rangA = 2. Так как rangA ≠ rangВ, система не имеет решений.

Ответ: а) б) система не имеет решений.