Министерство образования и науки Российской Федерации

Удмуртский государственный университет

Кафедра математики

–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

ВЫСШАЯ МАТЕМАТИКА

Ч а с т ь I

Элементы линейной,

векторной алгебры

и аналитической геометрии

Утверждено

в качестве учебного пособия

Воткинск

2013

УДК 51(075.8)

Ю 152

Учебное пособие предназначено для самостоятельной работы студентов. Содержит основные определения, формулы и задачи для самостоятельного решения по разделам курса высшей математики «Элементы линейной, векторной алгебры и аналитической геометрии».

Приведены примеры решений типовых задач и варианты заданий для расчетно-курсовой работы в пределах курса высшей математики.

Оглавление

Раздел 1. Элементы линейной и аналитической геометрии 4

1.1. Элементы линейной алгебры 4

1.1.1. Матрицы. Действия с матрицами 4

1.1.2. Определители 2-го и 3-го порядков 6

1.1.3. Метод Крамера решения систем алгебраических уравнений 7

1.1.4. Обратная матрица. Матричный метод решения

систем линейных алгебраических уравнений 7

1.1.5. Ранг матрицы. Решение систем линейных уравнений

методом Гаусса 10

1.2. Векторы 13

1.2.1. Понятие геометрического вектора 13

1.2.2. Модуль вектора 14

1.2.3. Базис 14

1.2.4. Разложение вектора по базису 14

1.2.5. Правая и левая тройки векторов 14

1.2.6. Проекция вектора на вектор 15

1.2.7. Ортонормированный базис 15

1.2.8. Скалярное произведение векторов и его свойства 15

1.2.9. Векторное произведение векторов и его свойства 16

1.2.10. Смешанное произведение векторов и его свойства 16

1.3. Прямоугольная декартовая система координат (ПДСК) 17

1.3.1. Определение прямоугольной декартовой системы координат 17

1.3.2. Нахождение координат вектора, заданного двумя точками 17

1.3.3. Линейные операции над векторами 18

1.3.4. Произведения векторов в ПДСК 18

1.4. Элементы аналитической геометрии 21

1.4.1. Плоскость в пространстве 21

1.4.2. Прямая в пространстве 22

1.4.3. Прямая на плоскости 22

1.4.4. Кривые 2-го порядка 25

1.4.5. Окружность 25

1.4.6. Эллипс 26

1.4.7. Гипербола 27

1.4.8. Парабола 28

Контрольная работа № 1 29

Контрольная работа № 2 33

Список литературы 35

Р а з д е л 1

Элементы линейной алгебры и аналитической геометрии

1.1. Элементы линейной алгебры

1.1.1. Матрицы. Действия с матрицами

Прямоугольная таблица вида 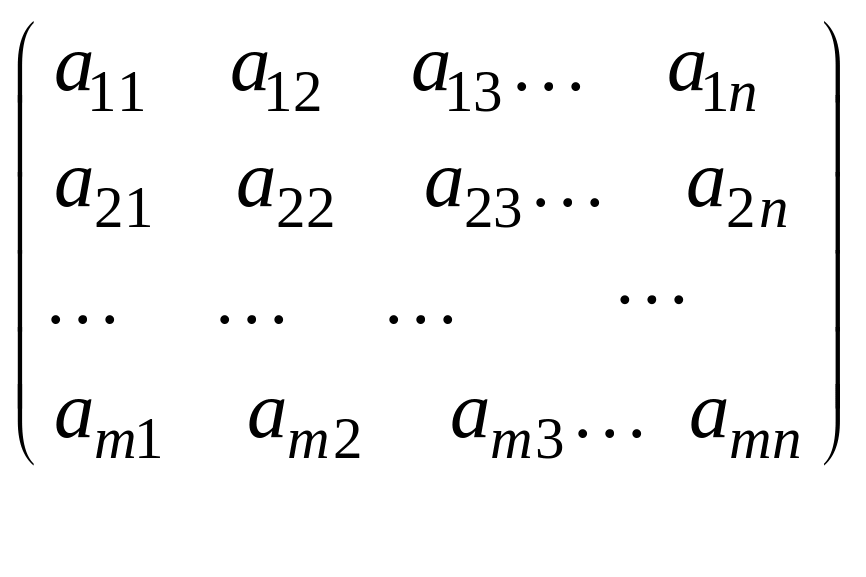называется матрицей, размерности Числа называются элементами матрицы.

Если в матрице число строк совпадает с числом столбцов, то такая матрица называется квадратной.

Суммой двух матриц А =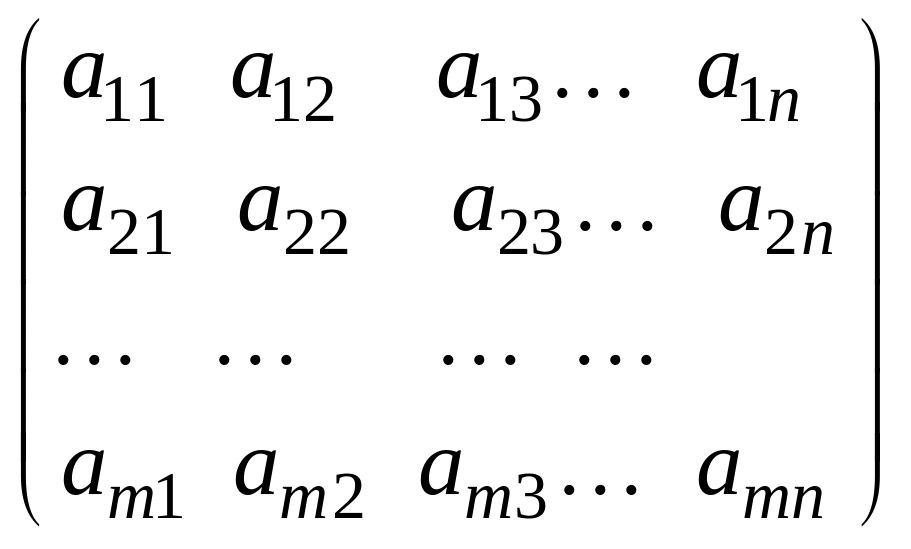 и В =

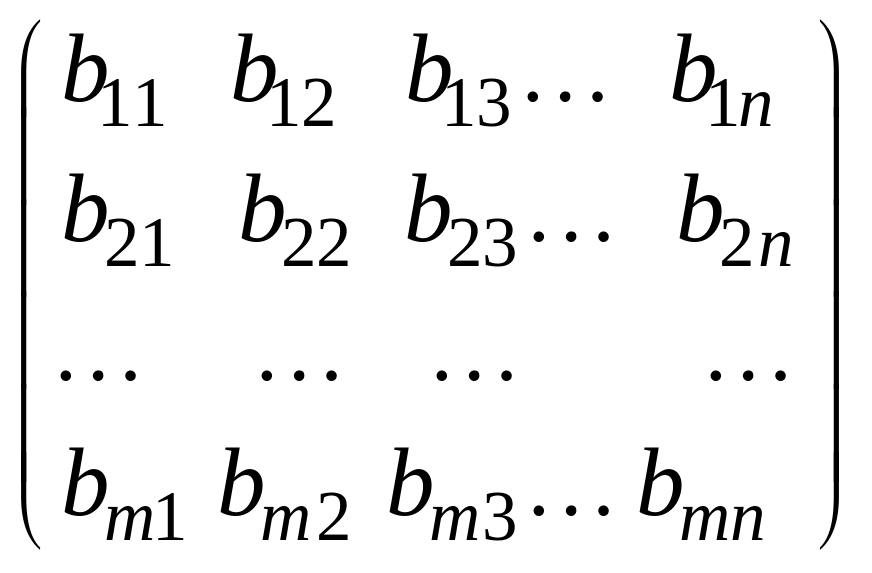
называется матрица

.

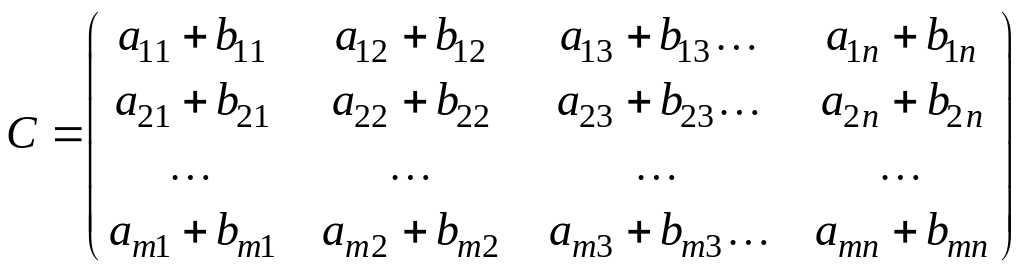Произведением числа на матрицу А называется матрица

.

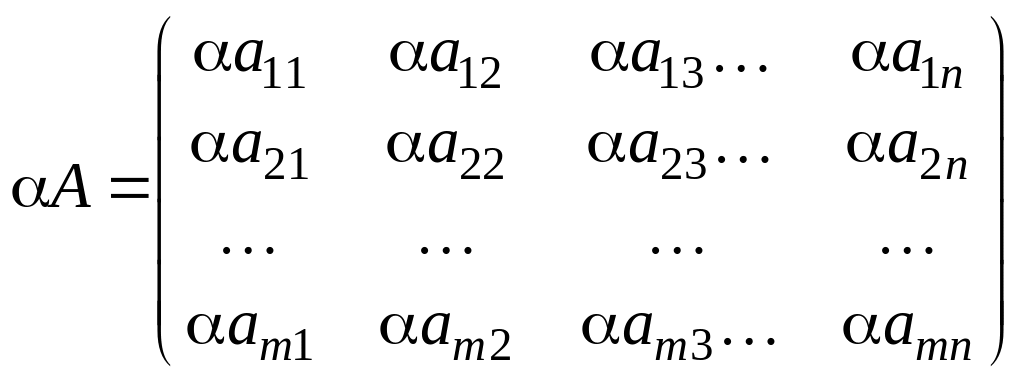Произведением двух матриц А и В называется матрица АВ, каждый элемент которой, стоящий в i-й строке и k-м столбце, равен сумме произведений соответственных элементов i-й строки матрицы А и k-го столбца матрицы В. При этом по отношению к произведению двух матриц не выполняется условие .

Перемножать можно только согласованные матрицы. Матрица А называется согласованной с матрицей В, если число столбцов матри-цы А равно числу строк матрицы В («ширина» матрицы А равна «высоте» матрицы В).

Элементарными преобразованиями матриц называются следующие преобразования: 1) прибавление к одной строке (столбцу) другой строки (столбца), умноженной на одно и то же постоянное число; 2) перестановка двух любых строк (столбцов) в матрице.

Две матрицы называются эквивалентными, если они получены одна из другой с помощью цепочки элементарных преобразований.

Пример

Даны матрица 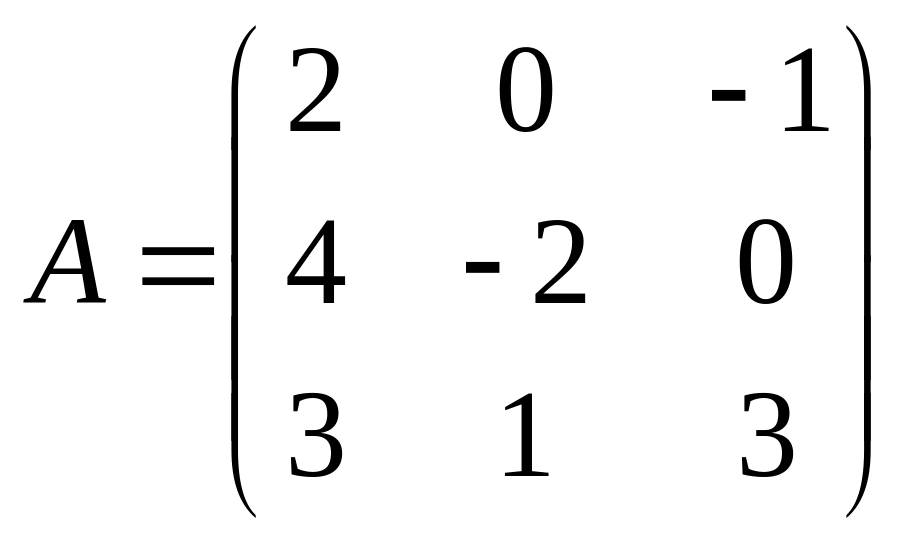и матрица 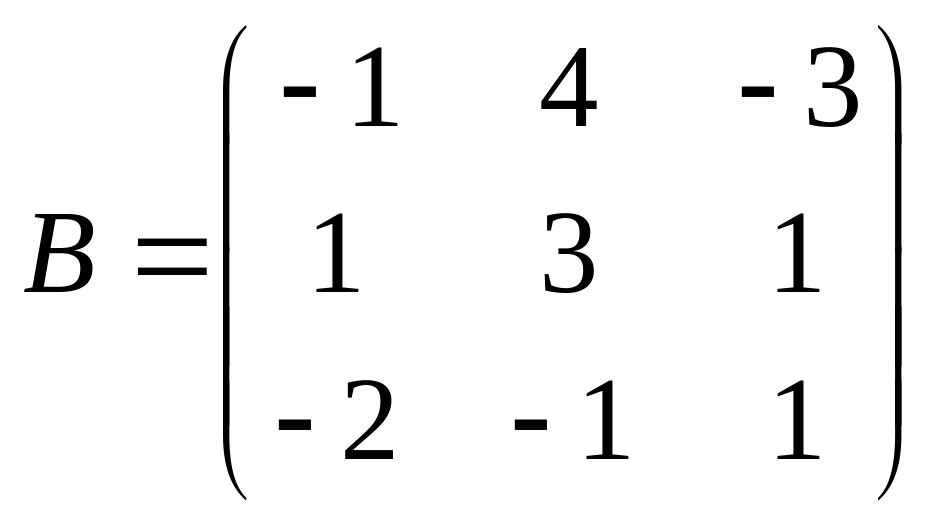Найти АВ.

Решение

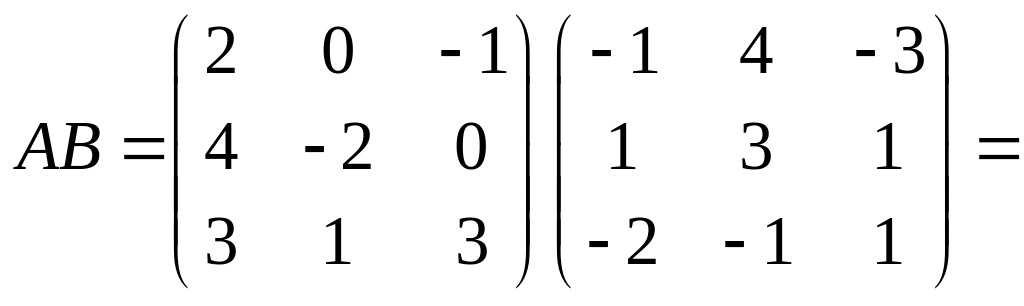
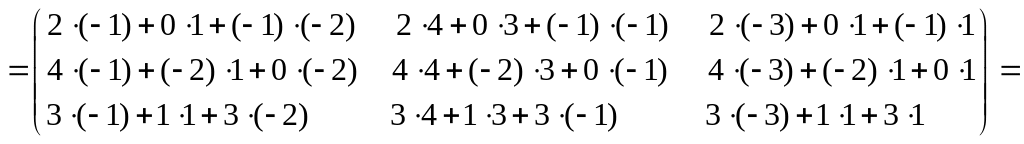
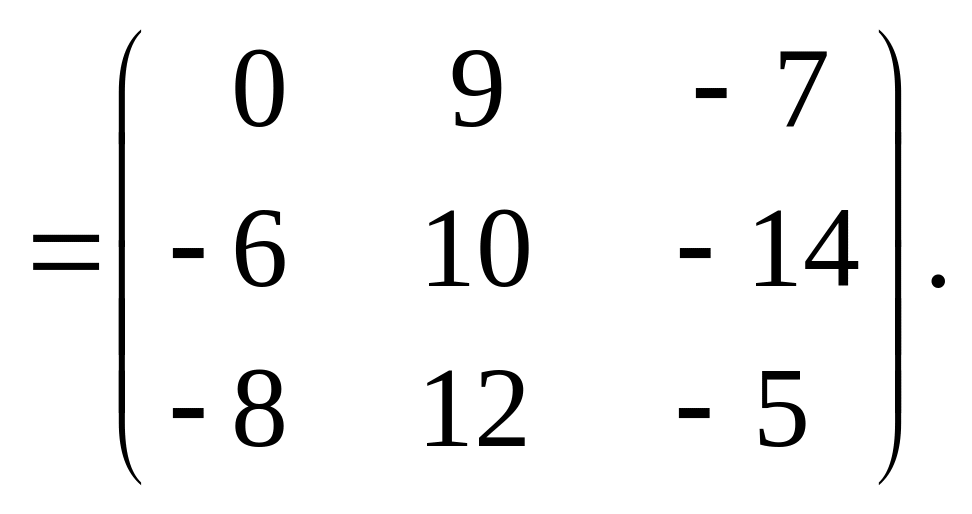
Ответ: .

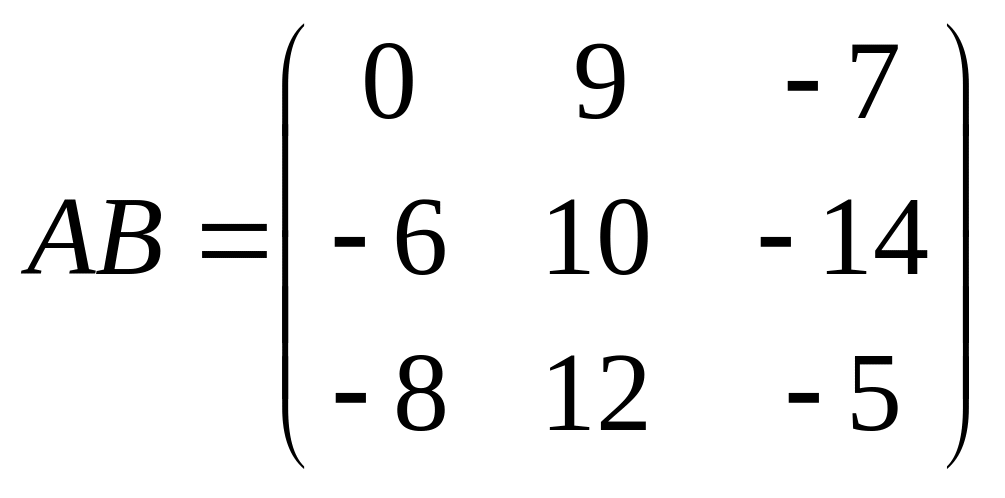1.1.2. Определители 2-го и 3-го порядков

Определитель второго порядка, соответствующий таблице эле-ментов , вычисляется следующим образом:

Определитель третьего порядка, соответствующий таблице элементов 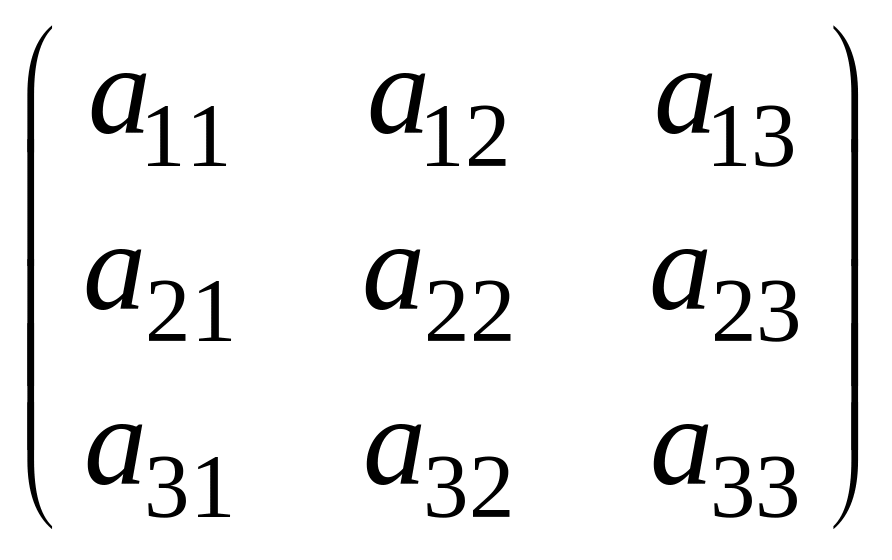, может быть вычислен разложением по первой строке:

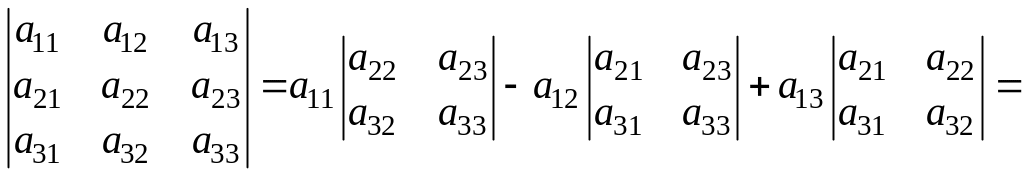
Определители выше третьего порядка также могут быть вычислены разложением по первой строке.

1.1.3. Решение систем алгебраических уравнений

методом Крамера