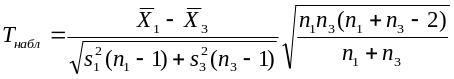Выполнение работы

Проверка статистических гипотез.

1.

Проверим гипотезу о равенстве дисперсий.

Даны дисперсии:

S₁²=

0,000139

S₂²=

0,000173

S₃²=

0,000166

n=50

l=3

Критерий Кочрена

Gнабл=

0,361925

Критическая точка Кочрена

G(a,k,l)=

0,4031

Gнабл<Gкр,

следовательно принимаем нулевую гипотезу, т.е. дисперсии равны

2.

Проверим гипотезу о равенстве средних для первой и третьей выборки.

H₀: X_cp1 = X_cp3

X_cp1=

5,9556

H₁: X_cp1 ≠ X_cp3

X_cp2=

5,9378

X_cp3=

5,9366

Tнабл=

7,692875

T_кр(,k), где k=n₁+n₂-2– число степеней свободы, для двусторонней критической области

Tkp=Т(0,05;98) =

1,98

|Tнабл|>Ткр,

следовательно отвергаем нулевую гипотезу

, т.е. средние первой и третьей выборок различны при данном уровне значимости

3.

H₀: X_cpi = D

H₁: X_cpi ≠ D

T_кр(,k), где k=n-1 – число степеней свободы, для двусторонней критической области

Т_кр = Т(0,05;49) = 2,009575237

для 1 выб.

Tнабл=

3,353455

|Тнабл|<Ткр,

отвергаем нулевую гипотезу , т.е. среднее первой выборки не совпадает с заданным стандартом

для 2 выб.

Tнабл=

-6,56516

|Тнабл|<Ткр,

отвергаем нулевую гипотезу, т.е. среднее второй выборки не совпадает с заданным стандартом

для 3 выб.

Tнабл=

-7,36219

|Тнабл|>Ткр,

отвергаем нулевую гипотезу, т.е. среднее третьей выборки не совпадает с заданным стандартом