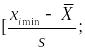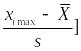Расчетная работа №4 проверка гипотезы о нормальности распределения генеральной совокупности. Критерии пирсона и колмогорова

Для выбранного в расчетной работе №1 товара:

1. Проверить гипотезу о нормальности распределения с помощью критерия согласия Пирсона при уровне значимости =0,01 и =0,05.

1. Расчеты необходимых параметров произведем с помощью программы EXCEL и составим таблицу теоретического распределения ( 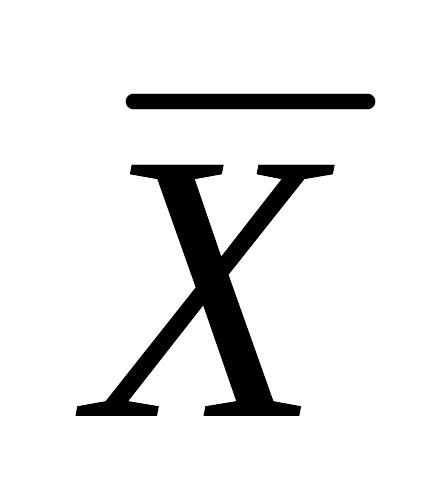=9,4496; s= 0,0155).

Xi min	Xi max	fi	mi			(x-xср)/s	Ф(х)	pi	ni	(ni-fi)2/ni
9,41	9,426	2	0,04	[-∞	;-1,521]	-1253,8	0	0,06409	3,2046	0,4528
9,426	9,442	14	0,28	[-1,521	;-0,49]	-1,5213	0,0641	0,24801	12,4	0,2064
9,442	9,458	20	0,4	[-0,49	;0,54]	-0,4899	0,3121	0,39381	19,691	0,0049
9,458	9,474	11	0,22	[0,54	;1,573]	0,54148	0,7059	0,29409	14,704	0,9332
9,474	9,49	3	0,06	[1,573	;∞]	1,57287	1	0,05787	2,8937	0,0039
										1,6011

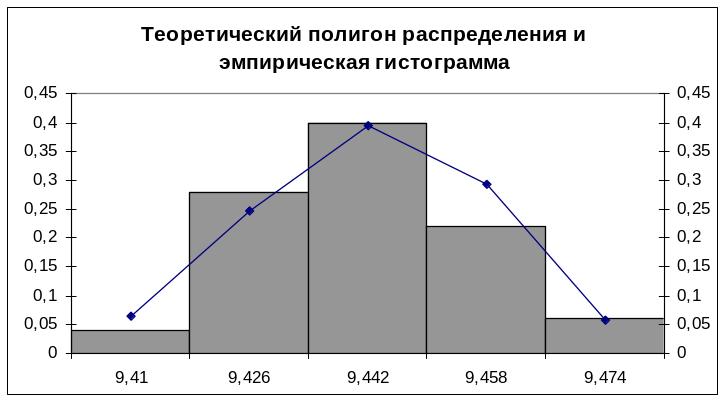
Рис. 1. Теоретический полигон распределения и эмпирическая гистограмма

2. Нулевая гипотеза Н₀: X  N( ,s²), т.е. совокупность имеет нормальное распределение, в качестве параметров которого взяты их наилучшие оценки.

Конкурирующая Н₁: совокупность не имеет нормальное распределение, в качестве параметров которого взяты их наилучшие оценки.

=1,6011

Степень свободы k=5-1-2=2.

Для =0,01, k=2, < =9,21. Для =0,05, k=2, < =5,9915.

Вывод: наблюдаемое значение не превысило критические точки критерия Пирсона, следовательно, принимаем нулевую гипотезу Н₀. Генеральная совокупность имеет нормальное распределение с параметрами =9,4496; s= 0,0155

РАСЧЕТНАЯ РАБОТА №5

Проверка статистических гипотез

1. Проверить гипотезу о равенстве дисперсий нескольких генеральных совокупностей при уровне значимости =0,05.

2. Проверить гипотезу о равенстве двух средних генеральных совокупностей при уровне значимости =0,05.

3. Проверить гипотезы о равенстве выборочных средних гипотетической генеральной средней D при уровне значимости =0,05.

Порядок выполнения работы

1. Сравнить дисперсии, определенные по выборкам в расчетной работе №1 (объемы выборок равны) по критерию Кочрена:

а) сформулировать нулевую и конкурирующую гипотезы;

б) определить наблюденное значение критерия Кочрена ;

в) определить критическое значение критерия Кочрена G_кр(,k,l), где -уровень значимости; k=n-1 – число степеней свободы; l – количество совокупностей;

г) сделать вывод о справедливости (при G_набл<G_кр) или несправедливости нулевой гипотезы.

2. Проверить гипотезу о равенстве двух средних для совокупностей, дисперсии которых равны:

а) сформулировать нулевую и конкурирующую гипотезы;

б) определить наблюденное значение критерия ;

в) определить критическую точку по таблице распределения Стьюдента T_кр(,k), где k=n₁+n₂-2 – число степеней свободы, для двусторонней критической области;

г) сделать вывод о справедливости (при |T_набл|<T_кр) или несправедливости нулевой гипотезы.

3. Проверить гипотезу о равенстве выборочной средней значению измеряемого размера D:

а) сформулировать нулевую и конкурирующую гипотезы;

б) определить наблюденное значение критерия ;

в) определить критическую точку по таблице распределения Стьюдента T_кр(,k), где k=n-1 – число степеней свободы, для двусторонней критической области;

г) сделать вывод о справедливости (при |T_набл|<T_кр) или несправедливости нулевой гипотезы.