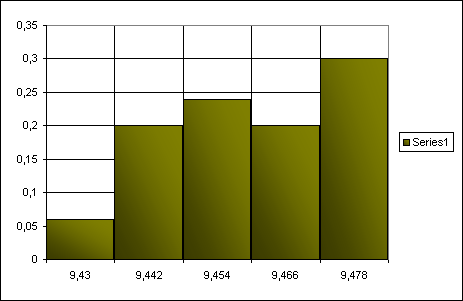Расчетная работа №1 выборочный метод оценки качества партии товара
Имеется три партии товара, основной размер которого D=9,45мм. Максимально допустимое верхнее отклонение ВО=0,05мм, Максимально допустимое нижнее отклонение НО=-0,05мм. Из каждой партии взята выборка, объема n=50 штук. Детали из выборки измерены прибором с ценой деления 0,01<0,1∙2δ, где 2δ=ВО-НО=0,1 – допуск, и результаты измерения x1, x2 и x3 представлены ниже.
Необходимо определить наиболее соответствующую требованиям партию, применив следующие критерии оценки:
Оценка мат. ожидания
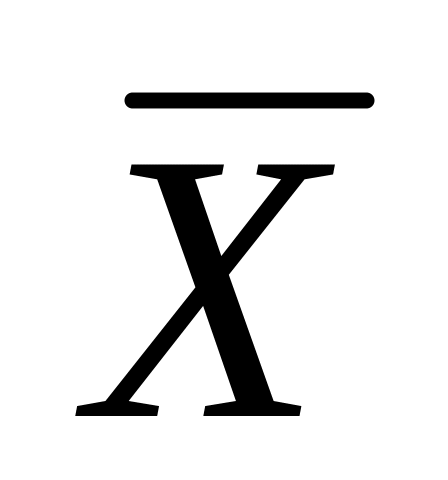наиболее близка к требуемому размеру
D.
Разброс параметров товара (среднеквадратическое отклонение) минимально.
Вероятность выхода из интервала допустимых отклонений минимальна.
Выборочные значения партий товаров:
Вариант №1 D=9,45 ВО=0,05 НО=-0,05 n=50
9,47; 9,47; 9,46; 9,48; 9,47; 9,46; 9,44; 9,46; 9,47; 9,47; 9,46; 9,47; 9,49; 9,47; 9,49; 9,46; 9,46; 9,47; 9,47; 9,45; 9,5; 9,48; 9,46; 9,46; 9,5; 9,47; 9,46; 9,48; 9,48; 9,49; 9,47; 9,43; 9,48; 9,48; 9,43; 9,46; 9,47; 9,47; 9,46; 9,46; 9,46; 9,46; 9,46; 9,44; 9,46; 9,46; 9,47; 9,48; 9,46; 9,46
9,49; 9,43; 9,45; 9,47; 9,47; 9,47; 9,46; 9,48; 9,46; 9,46; 9,47; 9,48; 9,47; 9,46; 9,45; 9,46; 9,46; 9,48; 9,47; 9,46; 9,49; 9,48; 9,46; 9,47; 9,46; 9,49; 9,48; 9,44; 9,48; 9,49; 9,45; 9,46; 9,45; 9,45; 9,46; 9,47; 9,45; 9,45; 9,47; 9,44; 9,46; 9,48; 9,48; 9,45; 9,47; 9,48; 9,45; 9,45; 9,49; 9,46
9,45; 9,43; 9,46; 9,41; 9,45; 9,46; 9,45; 9,46; 9,46; 9,44; 9,43; 9,44; 9,47; 9,46; 9,45; 9,46; 9,45; 9,45; 9,47; 9,45; 9,43; 9,44; 9,49; 9,45; 9,45; 9,42; 9,46; 9,49; 9,43; 9,44; 9,47; 9,45; 9,45; 9,44; 9,44; 9,45; 9,44; 9,43; 9,45; 9,47; 9,43; 9,45; 9,45; 9,45; 9,48; 9,44; 9,45; 9,45; 9,45; 9,45
1. Расчеты необходимых параметров произведем с помощью программы EXCEL
|
X1 |
|
X2 |
|
X3 |
|
9,47 |
|
9,49 |
|
9,45 |
|
9,47 |
|
9,43 |
|
9,43 |
|
9,46 |
|
9,45 |
|
9,46 |
|
9,48 |
|
9,47 |
|
9,41 |
|
9,47 |
|
9,47 |
|
9,45 |
|
9,46 |
|
9,47 |
|
9,46 |
|
9,44 |
|
9,46 |
|
9,45 |
|
9,46 |
|
9,48 |
|
9,46 |
|
9,47 |
|
9,46 |
|
9,46 |
|
9,47 |
|
9,46 |
|
9,44 |
|
9,46 |
|
9,47 |
|
9,43 |
|
9,47 |
|
9,48 |
|
9,44 |
|
9,49 |
|
9,47 |
|
9,46 |
|
9,47 |
|
9,46 |
|
9,46 |
|
9,49 |
|
9,45 |
|
9,45 |
|
9,46 |
|
9,46 |
|
9,46 |
|
9,46 |
|
9,46 |
|
9,45 |
|
9,47 |
|
9,48 |
|
9,45 |
|
9,47 |
|
9,47 |
|
9,47 |
|
9,45 |
|
9,46 |
|
9,45 |
|
9,5 |
|
9,49 |
|
9,43 |
|
9,48 |
|
9,48 |
|
9,44 |
|
9,46 |
|
9,46 |
|
9,49 |
|
9,46 |
|
9,47 |
|
9,45 |
|
9,5 |
|
9,46 |
|
9,45 |
|
9,47 |
|
9,49 |
|
9,42 |
|
9,46 |
|
9,48 |
|
9,46 |
|
9,48 |
|
9,44 |
|
9,49 |
|
9,48 |
|
9,48 |
|
9,43 |
|
9,49 |
|
9,49 |
|
9,44 |
|
9,47 |
|
9,45 |
|
9,47 |
|
9,43 |
|
9,46 |
|
9,45 |
|
9,48 |
|
9,45 |
|
9,45 |
|
9,48 |
|
9,45 |
|
9,44 |
|
9,43 |
|
9,46 |
|
9,44 |
|
9,46 |
|
9,47 |
|
9,45 |
|
9,47 |
|
9,45 |
|
9,44 |
|
9,47 |
|
9,45 |
|
9,43 |
|
9,46 |
|
9,47 |
|
9,45 |
|
9,46 |
|
9,44 |
|
9,47 |
|
9,46 |
|
9,46 |
|
9,43 |
|
9,46 |
|
9,48 |
|
9,45 |
|
9,46 |
|
9,48 |
|
9,45 |
|
9,44 |
|
9,45 |
|
9,45 |
|
9,46 |
|
9,47 |
|
9,48 |
|
9,46 |
|
9,48 |
|
9,44 |
|
9,47 |
|
9,45 |
|
9,45 |
|
9,48 |
|
9,45 |
|
9,45 |
|
9,46 |
|
9,49 |
|
9,45 |
|
9,46 |
|
9,46 |
|
9,45 |
Сред.знач. |
9,4668 |
|
9,4652 |
|
9,4496 |
|
0,0168 |
|
0,0152 |
|
0,0004 |
|
|
|
|
|
|
Дисперсия |
0,000214 |
|
0,000213 |
|
0,000241 |
Мин. |
9,43 |
|
9,43 |
|
9,41 |
Макс. |
9,5 |
|
9,49 |
|
9,49 |
|
|
|
|
|
|
h= |
0,014 |
0 |
0,012 |
0 |
0,016 |
Строим интервальные ряды для каждой выборки
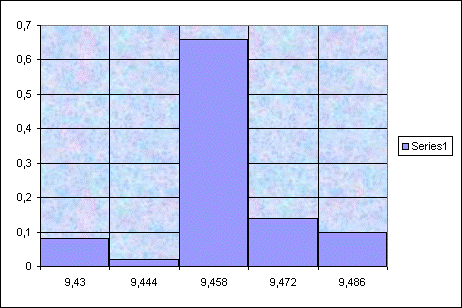
Для выборки №1
X1 i min |
x1 i max |
x1 i |
f1 i |
m1 i |
9,43 |
9,444 |
9,437 |
4 |
0,08 |
9,444 |
9,458 |
9,451 |
1 |
0,02 |
9,458 |
9,472 |
9,465 |
33 |
0,66 |
9,472 |
9,486 |
9,479 |
7 |
0,14 |
9,486 |
9,5 |
9,493 |
5 |
0,1 |
Для выборки №2
x2 i min |
x2 i max |
x2 i |
f2 i |
m2 i |
9,43 |
9,442 |
9,436 |
3 |
0,06 |
9,442 |
9,454 |
9,448 |
10 |
0,2 |
9,454 |
9,466 |
9,46 |
12 |
0,24 |
9,466 |
9,478 |
9,472 |
10 |
0,2 |
9,478 |
9,49 |
9,484 |
15 |
0,3 |
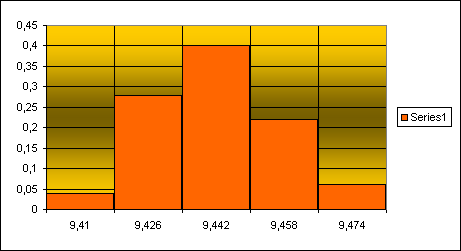
Для выборки №3
x3 i min |
x3 i max |
x3 i |
f3 i |
m3 i |
9,41 |
9,426 |
9,418 |
2 |
0,04 |
9,426 |
9,442 |
9,434 |
14 |
0,28 |
9,442 |
9,458 |
9,45 |
20 |
0,4 |
9,458 |
9,474 |
9,466 |
11 |
0,22 |
9,474 |
9,49 |
9,482 |
3 |
0,06 |
2. Считая, что выборки извлечены из нормально распределенной генеральной совокупности, рассчитать параметры статистического распределения:
а)
,
,
.
Построим гистограммы для выборок
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод: очевидно, что первая выборка имеет существенное отклонение от требуемого размера, по сравнению с остальными, и может быть исключена из дальнейшего рассмотрения. Для двух оставшихся выборок необходимо произвести более точный анализ.
3. Определить вероятность получения брака.
а) Смещение оценки математического ожидания от требуемого размера:
|
0,0168 |
|
Сред.квад.выб.1 |
0,01463 |
|
|x2 -D|= |
0,0152 |
|
Сред.квад.выб.2 |
0,014602 |
|
|x3 -D|= |
0,0004 |
|
Сред.квад.выб.3 |
0,015513 |
-D|=
б) Вероятный процент брака q=[0,5-Ф((δ-(| -D|))/σ)]∙100%.
q1= |
1,16% |
q2= |
0,86% |
q3= |
0,07% |
4. Сделать вывод.
Наименьший процент брака у третьей партии. Оценка мат. ожидания наиболее близка к требуемому размеру D у третьей партии. Среднеквадратическое отклонение наименьшее у второй партии. Следовательно, вторая и третья партии наилучшим образом соответствует требованиям.
В системе Газпрома из 1000 трубоукладчиков в порядке бесповторной выборки обследовано 100. В результате обследования получены следующие данные о распределении трубоукладчиков по уровню дневной выработки: |
|||||||
Группы работников по уровню дневной выработки, м2 |
5-7 |
7-9 |
9-11 |
11-13 |
Итого |
|
|
групповое среднее |
6,00 |
8,00 |
10,00 |
12,00 |
8,86666667 |
выборочное среднее |
|
|
8,22 |
0,75 |
1,28 |
9,82 |
20,07 |
|
|
xср -x ср груп |
-2,87 |
-0,87 |
1,13 |
3,13 |
|
|
|
Число работников в группе |
80,00 |
60 |
110 |
50 |
300 |
|
|
|
|
|
|
|
|
|
|
|
|||||||