7.1.4. Векторний добуток двох векторів

Векторним добутком двох векторів є вектор, який позначається

або = на відміну від позначення скалярного добутку .

Векторним добутком двох векторів називається третій вектор, що знаходиться так:

а) величина вектора , тобто модуль векторного добутку (модуль вектора ) рівна:

;

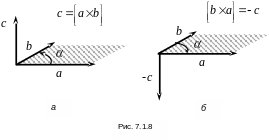
б) за напрямком вектор направлений перпендикулярно до площини, в якій лежать вектори та . Напрямок визначається за правилом правого гвинта (рис. 7.1.8).

Таким чином важливо, який вектор в добутку стоїть першим, тобто:

, .

На відміну від скалярного добутку, для якого виконується умова:

,

векторний добуток характеризується властивістю:

,

тобто переставлення векторів у добутку дає прямо протилежні вектори.

Таким чином важливо, який вектор в добутку стоїть першим, тобто:

, .

На відміну від скалярного добутку, для якого виконується умова:

,

векторний добуток характеризується властивістю:

,

тобто переставлення векторів у добутку дає прямо протилежні вектори.

Приклади: 1. Лінійна швидкість зв’язана з кутовою швидкістю співвідношенням, яке в векторній формі є векторним добутком кутової швидкості на радіус – вектор:

.

На рис. 1.1.6 розд.1 показано, яким чином знаходять напрямок вектора лінійної швидкості, що є векторним добутком двох інших векторів – кутової швидкості та радіус-вектора.

2. У загальному випадку силу Лоренца можна записати, використавши векторний добуток:

.

З останнього виразу видно, що вектор перпендикулярний до площини, в якій лежать вектори та .

3. Вектор, що показує напрямок розповсюдження електромагнітної хвилі (так званий вектор Пойнтінга) є векторним добутком векторів напруженостей електричного та магнітного поля:

.

Легко переконатись (рис. 7.1.9), що зміна взаємного розміщення векторів та призводить до зміни на протилежний напрямку розповсюдження електромагнітної хвилі. Це узгоджується з властивістю векторного добутку (як вектора) змінювати напрямок на протилежний при переставленні векторів у добутку.

7.1.5. Сума та різниця векторів

Сума двох векторів – це третій вектор, що знаходиться за „правилом паралелограма” (рис. 7.1.10, а).

Таким чином, сумою двох векторів є третій вектор, що побудований, як діагональ паралелограма, сторонами якого є ці два вектори. У випадку, коли є більш, ніж два вектори, можна користуватись ще й таким правилом: у кінець першого вектора переміщають (паралельним перенесенням) початок другого, в кінець другого, аналогічно, поміщають початок третього і т.д. Сумою векторів буде вектор, що з’єднає початок першого з кінцем останнього вектора. На рис. 7.1.10, б показано знаходження суми трьох векторів , та .

Різниця векторів – це третій вектор, що з’єднує кінці двох векторів, які виходять з однієї точки. Напрямок вектора різниці двох векторів вибирають у бік того вектора, від якого віднімають. Це видно з рис. 7.1.11, а та б. Різниця двох векторів за величиною (модулем) може бути більшою, ніж кожен з векторів, різницю яких знаходять. У багатьох фізичних задачах йдеться про зміну векторної фізичної величини за якийсь відрізок часу, яка є різницею кінцевого та початкового значення даної фізичної векторної величини.

Приклади. 1. У процесі руху положення матеріальної точки характеризується радіус-вектором. При переході від одного значення радіус-вектора у момент часу t₁ до у наступний момент часу t₂ вектор змінився на

.

Вектор, що з’єднує початкове та кінцеве положення радіус-вектора називається вектором переміщення (див. рис. 7.1.4). Вектор переміщення, таким чином, є зміною радіус-вектора чи приростом радіус-вектора.

2. При абсолютно пружному ударі (а. п. у.) кулька масою m відбивається від перешкоди зі швидкістю, що за величиною рівна швидкості падіння на перешкоду. При падінні перпендикулярно поверхні вектор швидкості змінюється на рівний за величиною та протилежний за напрямком (рис. 7.1.12, а).

Зміна імпульсу матеріальної точки рівна різниці векторів імпульсу після та до удару (рис. 7.1.12, б). Модуль цієї різниці (зміна імпульсу) буде вдвічі більшим, ніж величина імпульсу mV, тобто:

.

При абсолютно непружному ударі (а. н. у.) кулька зупиняється (як пластилінова кулька, що прилипла до стінки при ударі), а її швидкість стає рівною нулю (рис. 7.1.12 а та б). В цьому випадку величина зміни імпульсу буде вдвічі менша, ніж при абсолютно пружному ударі: , тобто .

Висновки цієї простої механічної задачі на визначення зміни імпульсу, що базуються на знаходженні різниці двох векторів, неодноразово використовуються в різних розділах фізики, наприклад при підрахунку тиску ідеального газу; тиску, що створює світло на поверхні з різними відбивальними властивостями тощо.