4.5Расчет переходного процесса

5.5.1. По виду вещественной составляющей (рисунок 5.5) производится предварительная оценка качества спроектированной САУ.

Рисунок 5.9

Оценка производится по следующим правилам.

1. Если при некотором значении частоты величина 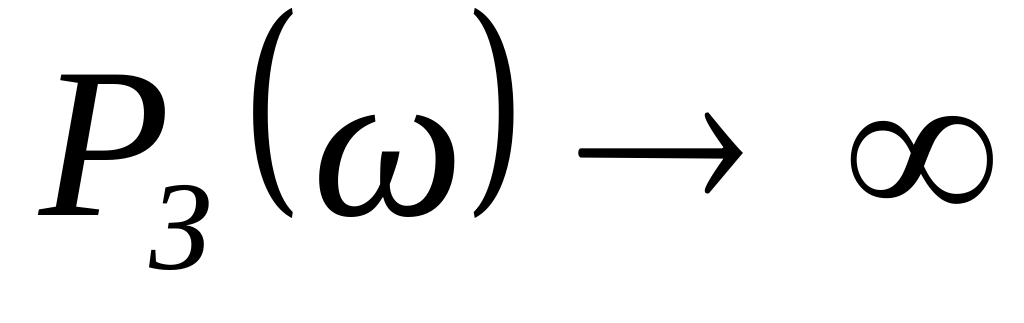, то система является неустойчивой;

2. Если функция положительна и невозрастающая (кривые 2,3), то есть выполняются соотношения , , то величина перерегулирования не более 18%.

3. Система стремится к устойчивому состоянию, если ;

4. Если функция изменяется по монотонно убывающей кривой 2, где имеют место соотношения , 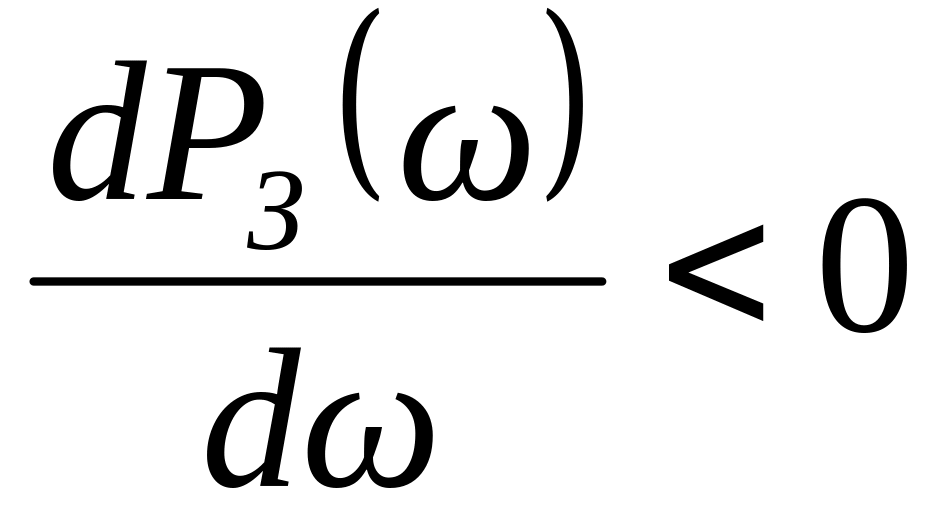и 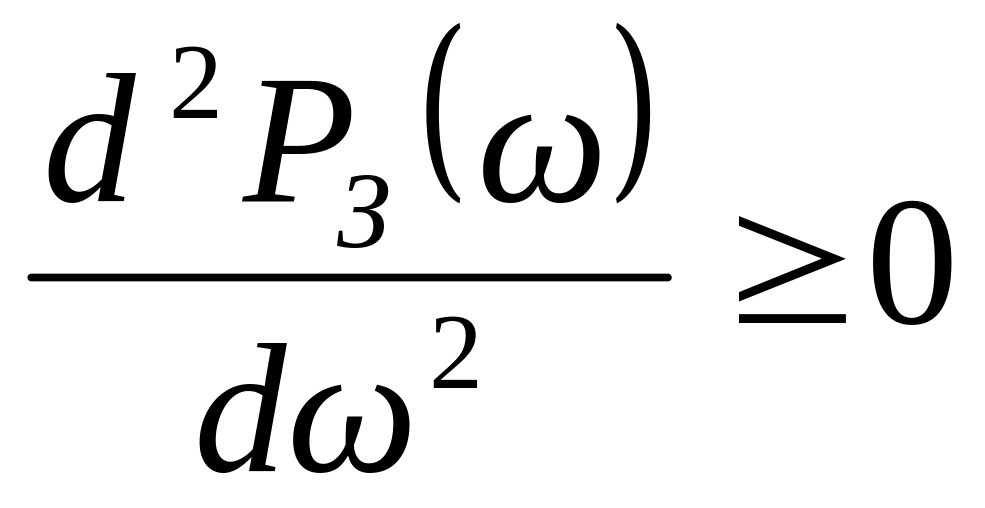, то регулируемый параметр стремится к установившемуся значению без перерегулирования, а время переходного процесса может быть оценена по формуле:

(5.11)

где – область существенных частот данной системы.

5. Если функция имеет вид кривой 3 с величиной максимума 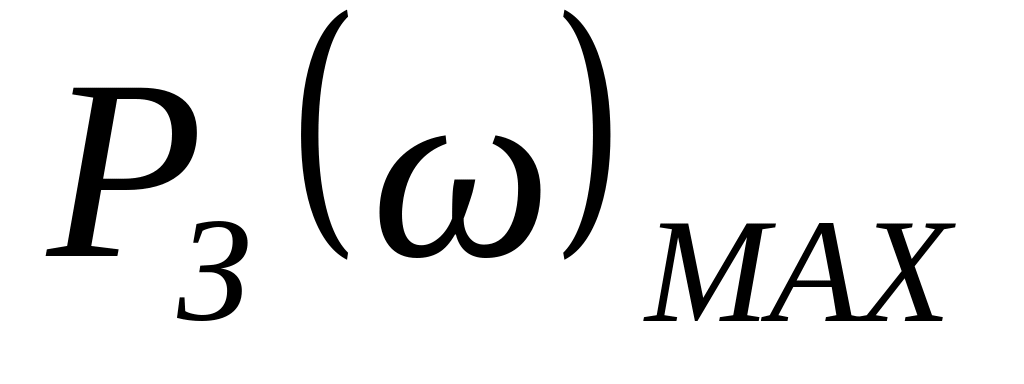_, то перерегулирование определяется соотношением:

   (5.12)

6. Если функция имеет вид кривой 4, где - интервал положительности, то время переходного процесса оценивается формулой:

(5.13)

5.5.2. Расчет переходного процесса в САУ и оценка ее динамических свойств и показателей качества можно производить методом, основанным на использовании вещественной частотной характеристики (вещественной составляющей передаточной функции)- математическим вычислением вещественной составляющей и ее интеграла, или приближенно (например, графическим методом типовых трапецеидальных характеристик [3]).

При приближенном решении задачи вещественная составляющая ПФ замкнутой САУ может быть либо вычислена, либо найдена графически (приложение В) по ЛАФЧХ разомкнутой системы и номограммам [4].

5.5.3. Для расчета переходных процессов кривую удобно представить в виде совокупности некоторого числа трапецеидальных частотных характеристик, после чего по таблицам [4] определяются соответствующие каждой из них переходные функции.

Правило приближенной замены кривой вещественной составляющей трапециями заключается в следующем (рисунок 5.6):

1. В окрестности экстремумов кривой прямолинейные отрезки располагаются параллельно оси w и отмечается начальная ордината .

2. Определяется крутизна боковой стороны трапеции по соотношению:

   (5.14)

3. По типовым характеристикам, соответствующим выбранным трапециям, в таблицу заносятся составляющие переходных процессов для единичных трапеций ( ПРИЛОЖНИЕ 5).

4. В соответствии с графиком Р_з (0) определяются масштабные коэффициенты и составляющие переходного процесса по формулам:

(5.20)

(5.21)

где  - нормированное время.

5. По сумме составляющих Х (t) определяется суммарный переходный процесс в системе.

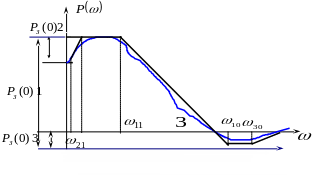
Рисунок 5.10

Рисунок 5.11

Для следящих систем (РЛС), как правило, регламентируется динамическая ошибка  _{дин доп .}

Пусть движение следящей системы характеризуется некоторыми допустимыми значениями:

D^!_2m - максимальная угловая скорость следящего вала;

D^!!_2m - максимальное угловое ускорение следящего вала.

Произвольное, в общем случае, движение вала D₂(t) можно представить эквивалентным гармоническим движением D_Э(t):

D_Э(t) = D_ЭМ (Sin  _Э t+  _Э) (168)

где D_ЭМ - амплитуда эквивалентного синусоидального движения;

 _Э - эквивалентная угловая частота.

Эквивалентность D_Э(t) движению D₂(t) понимается в том смысле, что два раза за период времени 2./  _Э = T_Э воспроизводятся максимальные угловая скорость и ускорение реального движения.

D^!_Э = d D_Э(t)/ dt = D_ЭМ  _Э Cos  _Э t = A Cos  _Э t (169)

D^!!_Э = d² D_Э(t)/ dt² = - D_ЭМ  ²_Э Sin  _Э t = B Sin  _Э t (170)

Приравнивая амплитуды скорости А и ускорения В эквивалентного движения максимально допустимым, получим:

D_ЭМ  _Э = D^!_2m ; D_ЭМ  ²_Э= D^!!_2m (171)

Откуда: D^!!_2m= D^!_2m  _Э .

Т.е. угловая частота эквивалентного движения  _Э= D^!!_2m / D^!_2m , а амплитуда эквивалентного гармонического движения D_ЭМ = D^!_2m /  _Э .

Передаточная функция по ошибке согласно определению понятия ошибки:

W_Д(p)= 1 / (1+W(p)= D_дин (р) / D₁(p) (172)

где D_дин (р) - динамическая ошибка слежения системы;

D₁(р) - динамическая фаза положения управляющего вала.

Очевидно для пригодной следящей системы, что D₁(р) D₂(p). Тогда динамическая ошибка:

D_дин (р)  1/ [!+W(p)] D₂ (p) (173)

Следовательно, для эквивалентного гармонического движения (по определению):

D_{М дин}= D _{Э М} /  1+ W(j) (174)

В области низких частот Т 1 и для ПФ САУ рассматриваемой РЛС (144) можно записать:

W(j)  K / (174a)

Из выражений (174) и (174a) следует:

K  D_{Э М}  _Э / D_{M дин} = D^!_2M / D_{M дин}

Так как D_{M дин}  _Э = D^!_2M , и принимая во внимание, что замена АФХ асимптотой дает отклонение 2^{1/ 2} (3 дб), получим окончательно:

K = 2^1/2 D^!_2M / D_{дин доп}