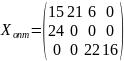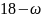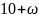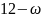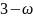- •Задача 2. Транспортная задача
- •Решение транспортной задачи с помощью метода потенциалов.
- •Решение задачи с помощью инструмента «Поиск решения» программного продукта Microsoft Excel.
- •1 Этап. Ввод исходных данных.
- •2 Этап. Вызов инструмента Поиск решения и ввод условий задачи
- •3 Этап. Решение задачи инструментом Поиск решения
- •4 Этап. Анализ полученного решения
- •Сравнение полученных результатов.
Министерство образования и науки Российской Федерации
(МИНОБРНАУКИ РОССИИ)
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ»
Институт информационных систем управления
Кафедра математических методов в управлении
по дисциплине: «Методы оптимальных решений»
ДОМАШНЯЯ РАБОТА №2
Вариант 20
на тему: «Транспортная задача»
Выполнила студентка очной формы обучения Сергиенко А.В. 2 курса 3 группы
|
____________________ (подпись) |
__________________________ (инициалы, фамилия) |
Принял |
____________________ (подпись) |
Е.Ю. Луценко |
Москва 2014 год
Задача 2. Транспортная задача
Решение транспортной задачи с помощью метода потенциалов.
Составить план перевозок, при котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах производства и общие транспортные расходы по доставке продуктов были бы минимальными.
Таблица 1. Исходные данные
|
b = |
39 |
21 |
28 |
16 |
|
а = |
42 |
7 |
7 |
2 |
9 |
c = |
36 |
8 |
9 |
5 |
9 |
||
38 |
6 |
7 |
1 |
2 |
В
правом столбце записаны компоненты
вектора a.
Каждая
i
–
я компонента
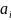 его
равна максимальному количеству единиц
продукта (максимальному предложению),
которое может отправить i-й
поставщик.
его
равна максимальному количеству единиц
продукта (максимальному предложению),
которое может отправить i-й
поставщик.
В
верхней строке находятся компоненты
вектора b.
Каждая
j
–
я компонента
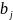 его
равна минимальному количеству единиц
продукта (максимальному спросу), которое
должен получить j-й
потребитель.
его
равна минимальному количеству единиц
продукта (максимальному спросу), которое
должен получить j-й
потребитель.
В
остальных местах таблицы 1 находятся
элементы матрицы С
удельных
затрат на транспортировку продукта
размера
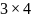 .
.
В матричном виде:
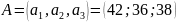
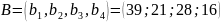
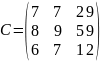
Общий
объем производства
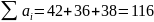 больше, чем требуется всем потребителям
больше, чем требуется всем потребителям
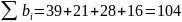 ,
т.е. имеем открытую модель транспортной
задачи. Для превращения ее в закрытую
вводим фиктивный пункт потребления с
объемом потребления 116 -104 = 12 единиц,
причем тарифы на перевозку в этот пункт
условимся считать равными нулю, помня,
что переменные, добавляемые к левым
частям неравенств для превращения их
в уравнения, входят в функцию цели с
нулевыми коэффициентами.
,
т.е. имеем открытую модель транспортной
задачи. Для превращения ее в закрытую
вводим фиктивный пункт потребления с
объемом потребления 116 -104 = 12 единиц,
причем тарифы на перевозку в этот пункт
условимся считать равными нулю, помня,
что переменные, добавляемые к левым
частям неравенств для превращения их
в уравнения, входят в функцию цели с
нулевыми коэффициентами.
Первое базисное допустимое решение, построенное по правилу «северо-западного угла», которое состоит в том, чтобы на каждом этапе мы максимально загружали «северо-западную клеточку».
Таблица 2. Первое базисное допустимое решение
-
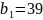
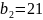
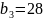
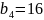
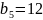
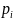
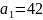
7
39
7
3
2
9
0
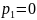
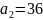
8
9
18
5
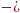

 18
189
0
+

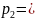 2
2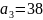
6
7
1
 +
10
+
102
 16
160
12
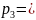 -2
-2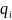
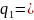 7
7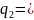 7
7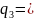 3
3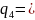 4
4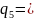 2
2
Обозначим
через
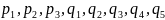 потенциалы поставщиков и потребителей
соответственно. Полагаем, что
потенциалы поставщиков и потребителей
соответственно. Полагаем, что
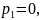 а
остальные потенциалы находим из следующих
условий для базисных неизвестных:
а
остальные потенциалы находим из следующих
условий для базисных неизвестных:
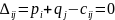
Имеем:
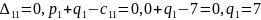
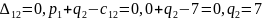
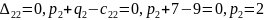
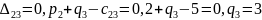
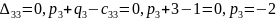

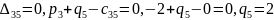
Затем по формуле вычисляем оценки всех свободных клеток:
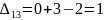
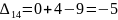
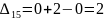
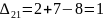
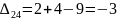
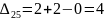

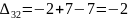
Находим наибольшую положительную оценку:
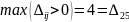
Для найденной свободной клетки (2,5) строим цикл пересчета – замкнутую ломаную линию. Это будет цикл с вершинами в клетках (2,5), (2,3), (3,3), (3,5). Ниже, на схеме выделены только вершинные клетки цикла пересчета.
18 |
|
10 |
16 |
|
|
|
|
|
|
|
|

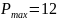
Таблица 3. Второе базисное допустимое решение
-
7
39
7

 3
32
+
9
0
8
9
+ 18
5
6
9
0
12
2
6
7
1
22
2
16
0
-2
7
7
3
4
- 2
Имеем:

Затем по формуле вычисляем оценки всех свободных клеток:
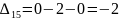
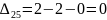
Находим наибольшую положительную оценку:
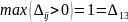
Для найденной свободной клетки (1,3) строим цикл пересчета. Это будет цикл с вершинами в клетках (1,3), (1,2), (2,2), (2,3).
3 |
|
18 |
6 |
|
|
|
|
0 |
|
21 |
3 |
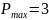
Таблица 4. Третье базисное допустимое решение
-
7
39

7
2
+ 3
9
0
8
+
9
21
5
3
9
0
12
3
6
7
1
22
2
16
0
-1
7
6
2
3
- 3
Следующим шагом является нахождение потенциалов:
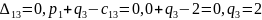
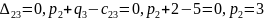
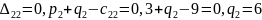
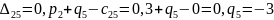
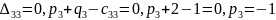
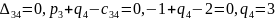
Оценки для свободных клеток:
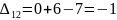
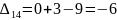
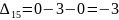

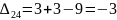
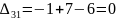

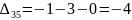
Наибольшая положительная оценка:
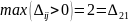
Для найденной свободной клетки (2,1) строим цикл пересчета. Это будет цикл с вершинами в клетках (2,1), (2,3), (1,3), (1,1).
39 |
3 |
|
3 |
|
|
|
|
36 |
6 |
|
0 |
Таблица 5. Четвертое базисное допустимое решение
-
7
36
7
+
2
6
9
0
8
+ 3
9
21
5
9
0
12
1
6
7
1
22
2
16
0
-1
7
8
2
3
- 1
Находим потенциалы:
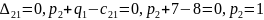
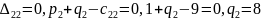
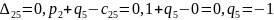
Далее находим оценки свободных клеток.
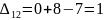
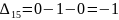

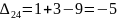
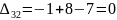
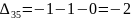
Наибольшая положительная оценка:
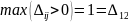
Для найденной свободной клетки (1,2) строим цикл пересчета. Это будет цикл с вершинами в клетках (1,2), (1,1), (2,1), (2,2).
36 |
|
3 |
21 |
|
|
|
|
15 |
|
24 |
0 |
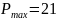
Таблица 6. Пятое базисное допустимое решение
-
7
15
7
21
2
6
9
0
8
24
9
5
9
0
12
1
6
7
1
22
2
16
0
-1
7
7
2
3
- 1
Имеем:
Оценки свободных клеток:
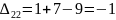

Опорный
план является оптимальным, так как все
оценки свободных клеток
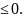
Итак,
оптимальное базисное допустимое решение