2.3 Применение интерполяционных сплайнов

Интерполяционный кубический сплайн – это совокупность полиномов третьей степени вида:

где S- значение аппроксимируемой функции в узлах, t_i - значения аргумента в узлах, b,c,d– коэффициенты сплайна для-го участка, i=0,1,2... – номер участка, n– число точек в таблице аппроксимируемой функции, считая с нуля.

Таким образом, полиномы строятся для каждого -го участка, но так, чтобы в совокупности получалась гладкая функция.

Построение интерполяционного сплайна состоит в определении коэффициентов b,c,d . Тогда для каждого i-го участка по формуле можно будет найти значение сплайна для любого t, которое и будет приближенным значением функции .

Дифференцированием аппроксимирующей функции определяется скорость звена.

В частности, значения производной в узлах .

Поскольку операция дифференцирования понижает порядок полинома, то для вычисления ускорения с большей точностью для функции строится свой сплайн и ускорение вычисляется как первая производная уже от него.

Результаты аппроксимации данным методом представлены на рис. 2.5. и табл. 2.6. Как и следует из названия, этот сплайн дает интерполирующую аппроксимацию. Операция сглаживания с его помощью не возможна. Этот метод целесообразно применять в тех случаях, когда аппроксимирующую функцию надо проводить в точности по исходным точкам. И здесь на графиках производных наблюдается отсутствие периодичности.

Таблица 2.6

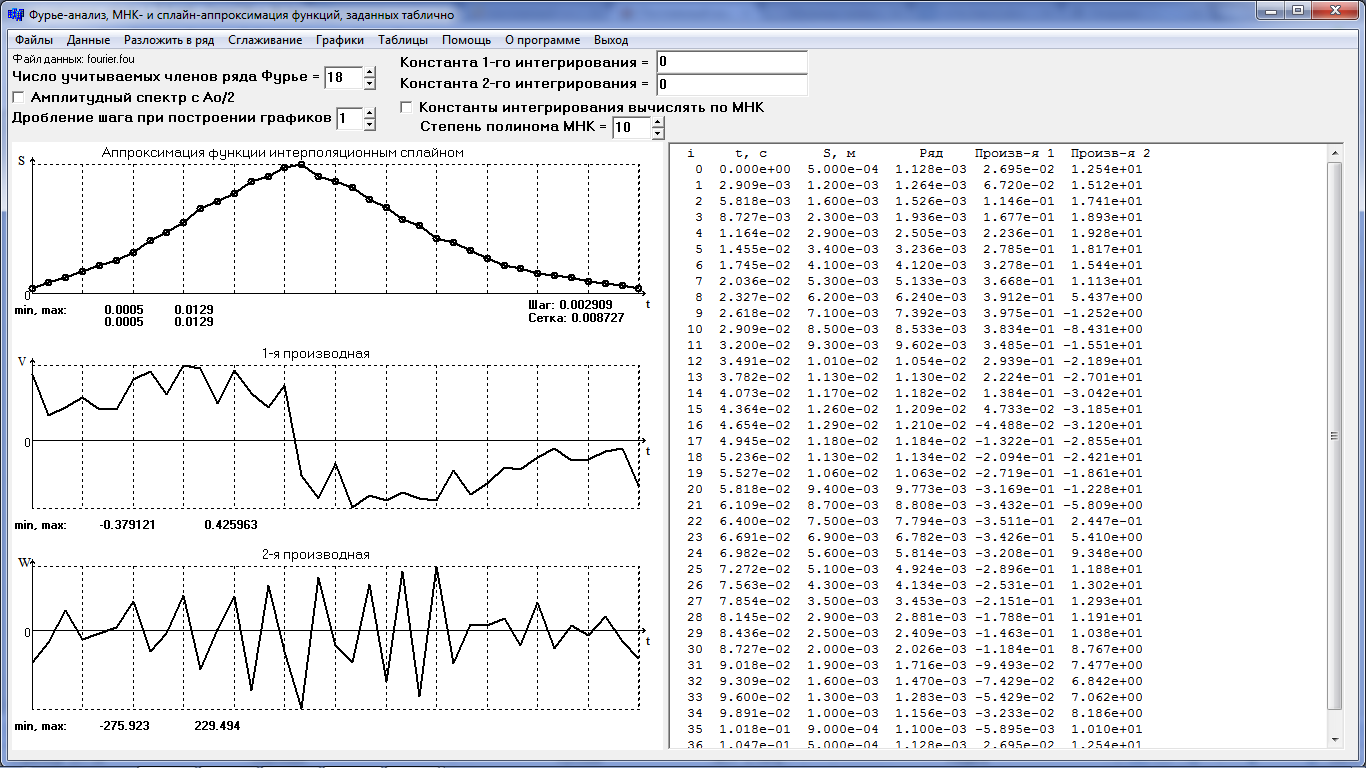
Рис.2.5

2.4 Аппроксимация сглаживающим сплайном

Для построения сглаживающего сплайна формируется так называемый коридор, то есть для каждой точки задается максимально- и минимально допустимое значение функции и сам сплайн строится так, чтобы его график проходил между точками этого коридора, минимизируя энергию изгиба.

Результаты аппроксимации показаны на рис.2.7 и табл. 2.7. Функция аппроксимирована удовлетворительно, со сглаживанием. Однако на графиках производных проявляется основной недостаток – нарушение периодичности, в то время, как функция в данном случае периодична по своей сути.

Таблица 2.7

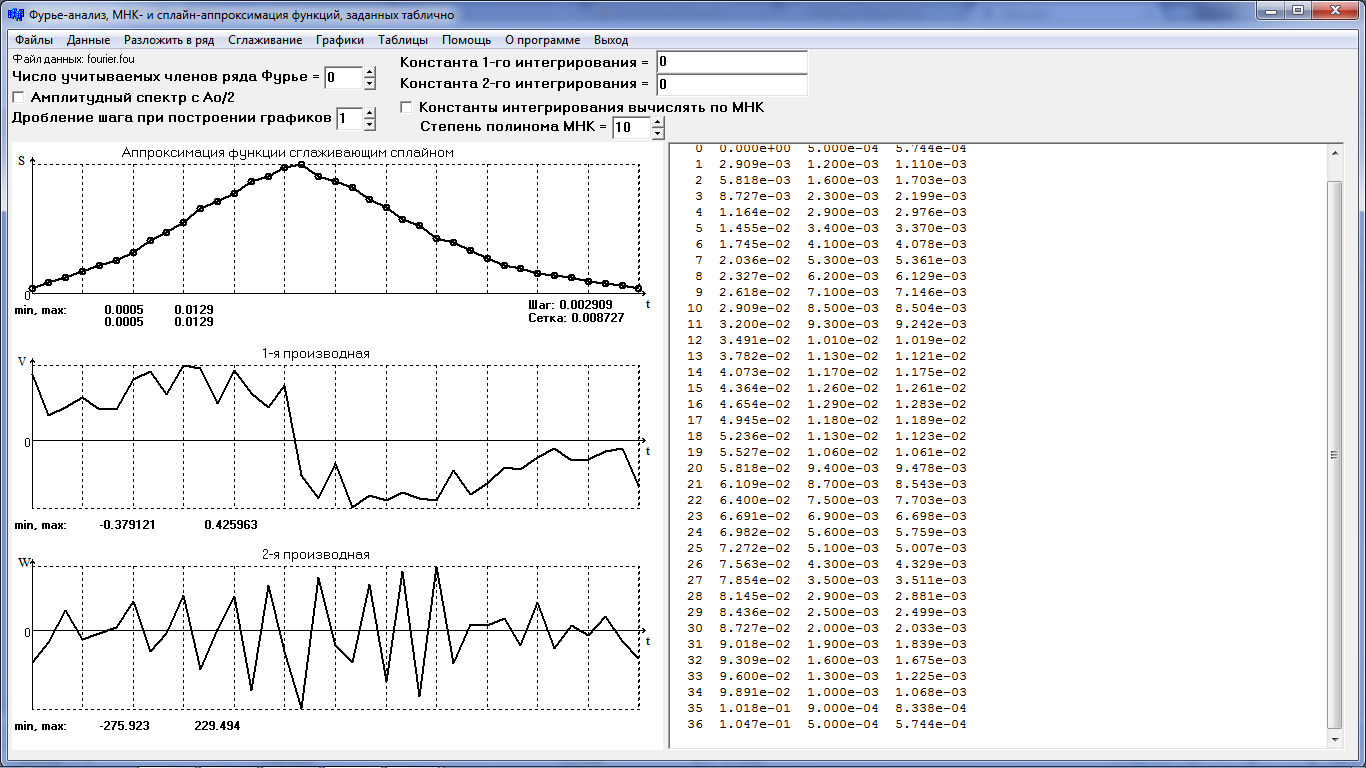
рисунок 2.7

Выводы к работе:

1. Функция аппроксимировалась четырьмя методами, три из которых позволяют производить сглаживающую аппроксимацию.

2. Ряд Фурье позволяет производить интерполирующую и сглаживающую аппроксимацию, причём для сглаживающей аппроксимации следует при разложении учитывать лишь первые основные частоты, определяемые по амплитудному спектру.

3. Ряды Фурье хорошо подходят для аппроксимации гладких функций.

4. Ряды Фурье в первую очередь целесообразно применять для аппроксимации периодических функций.

5. С помощью полиномов аппроксимация самой функции выполнена удовлетворительно, но на графиках производных проявился основной недостаток – нарушение периодичности, в то время, как функция в данном случае периодична по своей сути.

6. Интерполяционные сплайны целесообразно применять в тех случаях, когда аппроксимирующую функцию надо проводить в точности по исходным точкам. Этот метод тоже не обеспечил условие периодичности производных.

7. Сглаживающий сплайн хорошо сглаживает функцию, но несколько хуже – производные. Результаты сглаживания сильно зависят от конфигурации коридора.

8. В данной лабораторной работе наилучшие результаты получены при аппроксимации рядом Фурье.

16