1. Структурный анализ механизма

На рис.1.1, а представлена структурная схема исследуемого трехзвенного механизма с тремя подвижными звеньями.

Рис.1.1

Исследуем механизм на наличие пассивных связей, составив его матрицу смежности. Матрица смежности представлена в табл. 1.1.

Таблица 1.1

N	1	2	3
1	-
2		-
3			-

Число степеней свободы определяется по формуле Чебышева для плоских механизмов:

где n – количество подвижных звеньев, p1 и p2 – количество кинематических пар пятого и четвёртого класса соответственно.

Рис.1.2.

На рис.1.2 произведено структурное деление механизма

2. Кинематический анализ механизма

Кинематический анализ производится экспериментально-теоретически. Функцию положения ползуна 3 в зависимости от угла поворота кривошипа 1 получаем экспериментально. Результаты эксперимента представлены в таблице 2.1.

Таблица 2.1

S	φ1̊		S	φ1̊		S	φ1̊		S	φ1̊
	10			100			190			280
	20			110			200			290
	30			120			210			300
	40			130			220			310
	50			140			230			320
	60			150			240			330
	70			160			250			340
	80			170			260			350
	90			180			270			360

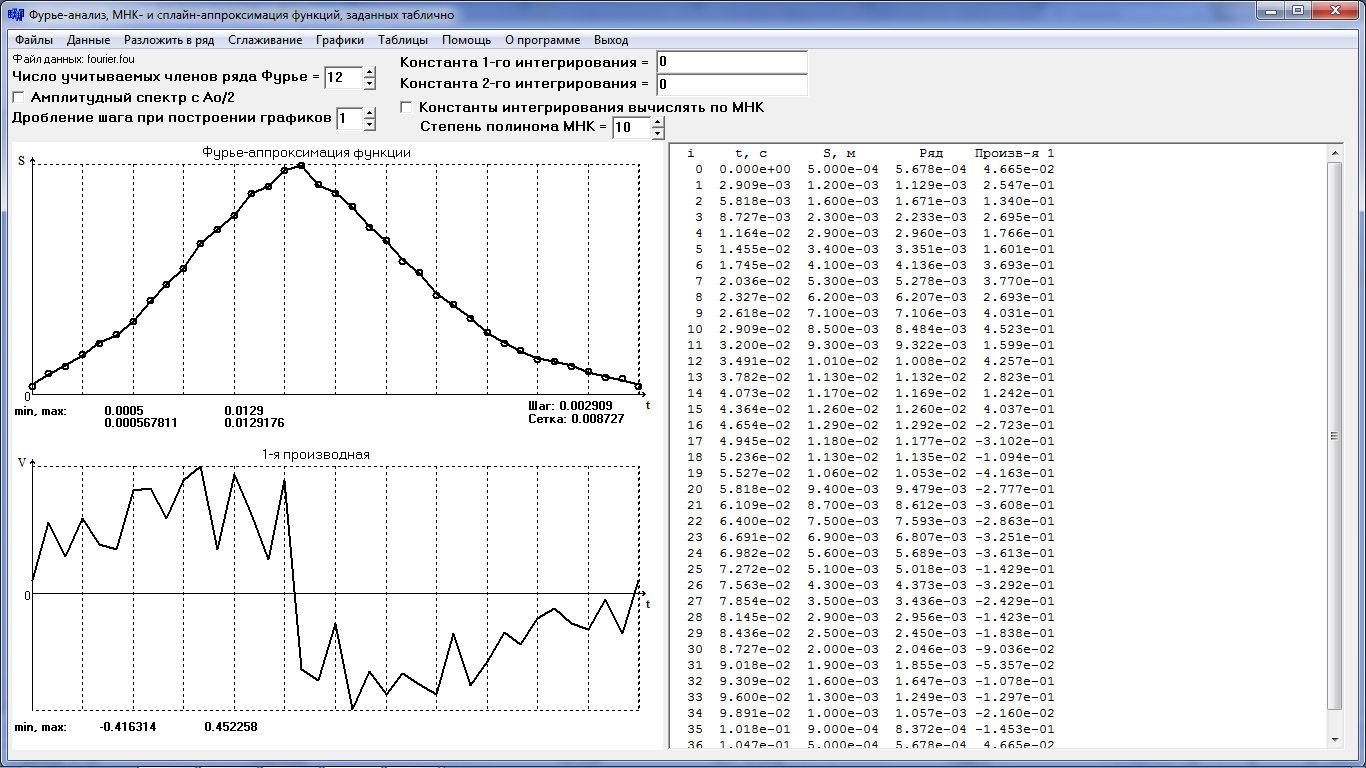
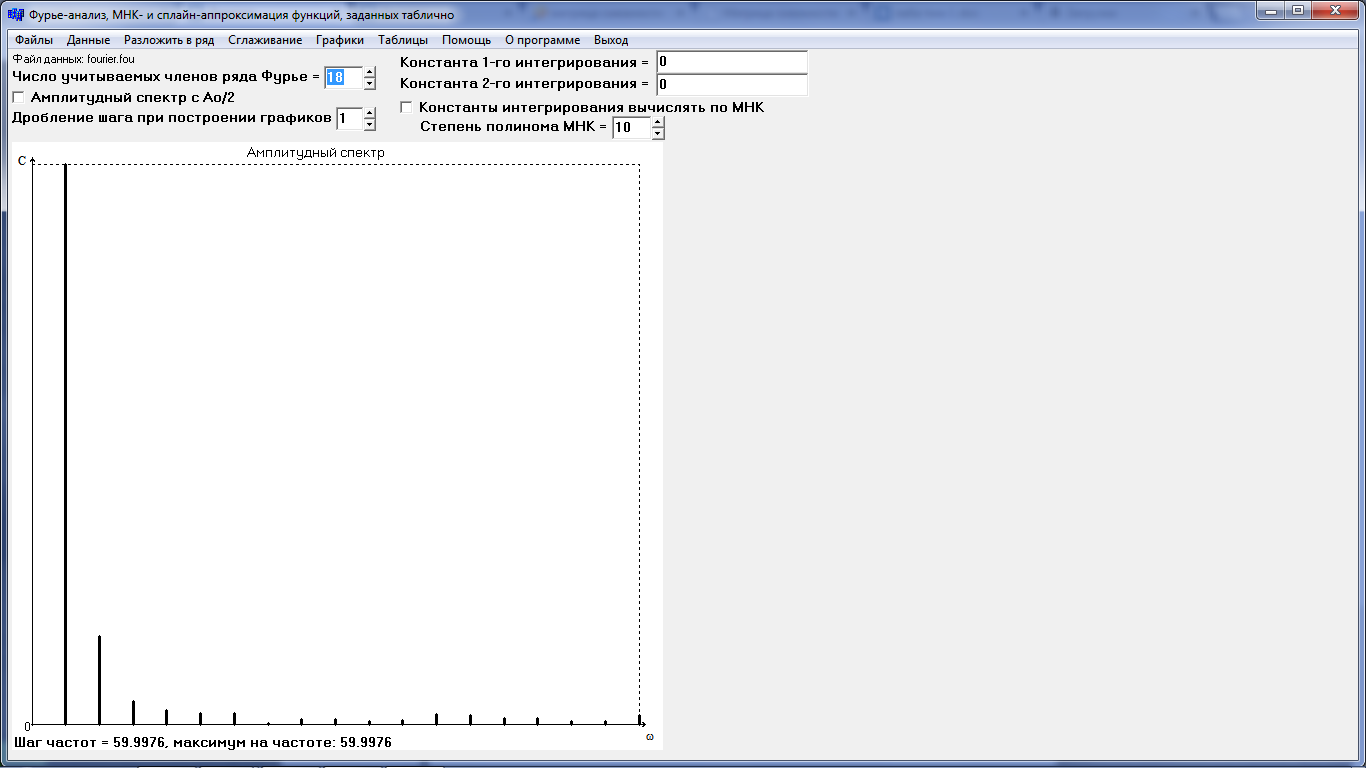
Полагая , что кривошип вращается с постоянной угловой скоростью ω₁=60 с^-1 , следовательно , φ₁=ω₁ t , получим функцию положения от времени S(t) . Для этого вычислим шаг таблицы по времени :

∆t=∆ φ_{1 рад} / ω₁ = 0.17453 / 60 = 0.002909 с ,

где ∆ φ_{1 рад} =∆ φ₁̊ π / 180 = 10π / 180 = 0.17453 рад .

Для аналитической обработки функции S(t) проведем аппроксимацию её таблицы четырьмя методами . Обработку данных эксперимента проведем с помощью программы ApproxFSP .