Завдання для самостійної роботи

1. Побудувати графік нормальної функції щільності розподілу f(x) при x, що змінюється від 20 до 40 із кроком 1 при =3.

2. Знайти імовірність того, що з'явиться випадкова величина x 42 при нормальному законі розподілу імовірностей з М=40 і .

3. Побудувати діаграму нормальної функції щільності імовірності при М=40 і .

4. Знайти квантиль для р=09087089 і нормального розподілу із задачі 2.

5. Побудувати діаграму інтегральної функції розподілу імовірності при М=30 і .

6. Знайти нормалізоване значення x, якщо x=21, М=20, .

Контрольні питання

1. Що називають законом розподілу випадкової величини?

2. Що значить «нормальний» закон розподілу?

3. Який графік даного розподілу?

4. Чому дорівнює математичне очікування?

5. Чому дорівнює дисперсія?

6. Чому дорівнює мода і медіана?

Лабораторна робота № 5

«Використання електронних таблиць Excel для побудови вибіркових функцій розподілу»

Мета роботи: Побудувати вибіркові функції розподілу за допомогою MS Excel.

Теоретичні відомості

Розглянуті раніше розподіли імовірностей випадкової величини (ВВ) опираються на знання закону розподілу ВВ. Для практичних задач таке знання – рідкість. Тут закон розподілу звичайно невідомий, або відомий з точністю до деяких невідомих параметрів. Зокрема, неможливо розрахувати точне значення відповідних імовірностей, тому що не можна визначити кількість загальних і сприятливих ісходів. Тому вводиться статистичне визначення імовірності. По цьому визначенню імовірність дорівнює відношенню числа випробувань, у яких подія відбулася, до загального числа зроблених випробувань. Така імовірність називається статистичною частотою.

Статистичним розподілом вибірки називають перелік варіант і відповідних їм частот або відносних частот.

Зв'язок між емпіричною функцією розподілу й функцією розподілу (теоретичною функцією розподілу) така ж, як зв'язок між частотою події і його імовірністю.

Для побудови вибіркової функції розподілу весь діапазон зміни випадкової величини X (вибірки) розбивають на ряд інтервалів (кишень) однакової ширини. Кількість інтервалів звичайно вибирають не менш 3 і не більше 15. Потім визначають число значень випадкової величини X, що потрапили в кожний інтервал (абсолютна частота, частота інтервалів).

Сума всіх абсолютних частот називають об'ємом вибірки (тобто кількість всіх об'єктів вибірки). Наприклад, у наступній гістограмі осі ординат відкладені n_i / h (h – довжина інтервалу), отже, об'єм вибірки дорівнює 2 * (1 + 2 + 4 + 5) = 24.

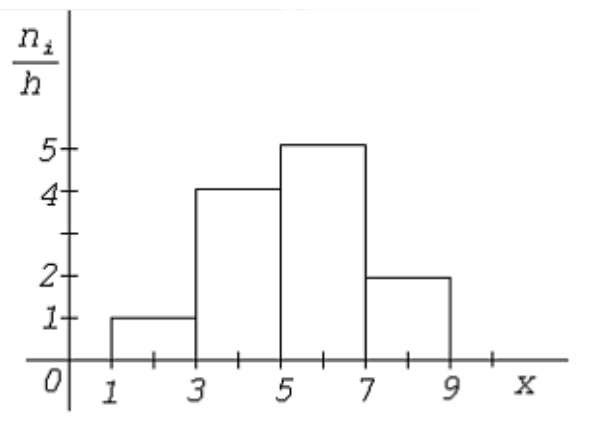
Частота інтервалів – число, що показує скільки разів значення, що ставляться до кожного інтервалу угруповання, зустрічаються у вибірці. Поділивши ці числа на загальну кількість спостережень (n), знаходять відносну частоту (частість) влучення випадкової величини X у задані інтервали.

По знайдених відносних частотах будують гістограми вибіркових функцій розподілу.

Гістограма розподілу частот – це графічне подання вибірки, де по осі абсцис (ОХ) відкладені величини інтервалів, а по осі ординат (ОУ) – величини частот, що попадають у даний класовий інтервал. При збільшенні нескінченно розміру вибірки вибіркові функції розподілу перетворюються в теоретичні: гістограма перетворюється в графік щільності розподілу.

Накопичена частота інтервалів – це число, отримане послідовним підсумовуванням частот у напрямку від першого інтервалу до останнього, до того інтервалу включно, для якого визначається накопичена частота.

В Excel для побудови вибіркових функцій розподілу використовуються спеціальна функція ЧАСТОТА й процедура Гістограма з пакета аналізу.

Функція ЧАСТОТА (масив_даних, двійковий_масив)обчислює частоти появи випадкової величини в інтервалах значень і виводить їх як масив цифр, _де

• масив_даних — це масив або посилання на множину даних, для яких обчислюються частоти;

• двійковий_масив — це масив інтервалів, по яких групуються значення вибірки.

Процедура Гістограма з Пакету аналізу виводить результати вибіркового розподілу у вигляді таблиці й графіка. Параметри діалогового вікна Гістограма:

• Вхідний діапазон - діапазон досліджуваних даних (вибірка);

• Інтервал кишень – діапазон комірок або набір граничних значень, що визначають обрані інтервали (кишені). Ці значення повинні бути уведені в зростаючому порядку. Якщо діапазон кишень не був уведений, то набір інтервалів, рівномірно розподілених між мінімальним і максимальним значеннями даних, буде створений автоматично.

• вихідний діапазон призначений для уведення посилання на ліву верхню комірку вихідного діапазону.

• перемикач Інтегральний відсоток дозволяє встановити режим включення в гістограму графіка інтегральних відсотків.

• перемикач Вивід графіка дозволяє встановити режим автоматичного створення убудованої діаграми на аркуші, що містить вихідний діапазон.

Завдання 1.

Побудувати емпіричний розподіл ваги студентів у кілограмах для наступної вибірки: 64, 57, 63, 62, 58, 61, 63, 70, 60, 61, 65, 62, 62, 40, 64, 61, 59, 59, 63, 61.

Рішення

1. В комірку А1 уведіть слово Спостереження, а в діапазон А2:А21 — значення ваги студентів.

2. В комірку В1 уведіть назви інтервалів Вага, кг. У діапазон В2:В8 уведіть граничні значення інтервалів (40, 45, 50, 55, 60, 65, 70).

3. Уведіть заголовки створюваної таблиці: в комірки С1 — Абсолютні частоти, в комірки D1 — Відносні частоти, в комірки E1 — Накопичені частоти.

4. За допомогою функції Частота заповніть стовпець абсолютних частот, для цього виділите блок комірок С2:С8. З панелі інструментів Стандартна викличте Майстер функцій (кнопка fx). У діалоговому вікні, що з'явилося, виберіть категорію Статистичні й функцію ЧАСТОТА, після чого натисніть кнопку ОК. Курсором миші в робоче поле Масив_даних уведіть діапазон даних спостережень (А2:А21). У робоче поле Двійковий_масив мишею введіть діапазон інтервалів (В2:В8). Ліворуч на клавіатурі послідовно натисніть комбінацію клавіш Ctrl+Shift+Enter. У стовпці C повинен з'явитися масив абсолютних частот.

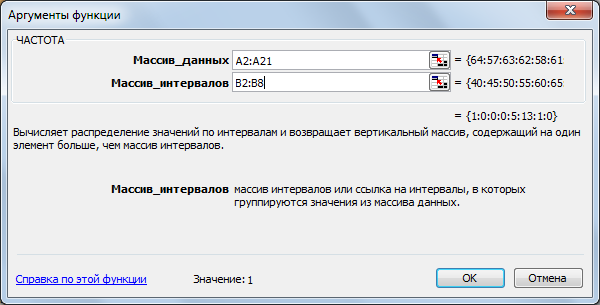
Рисунок 5.1 – Вигляд діалогового вікна для введення параметрів функції ЧАСТОТА

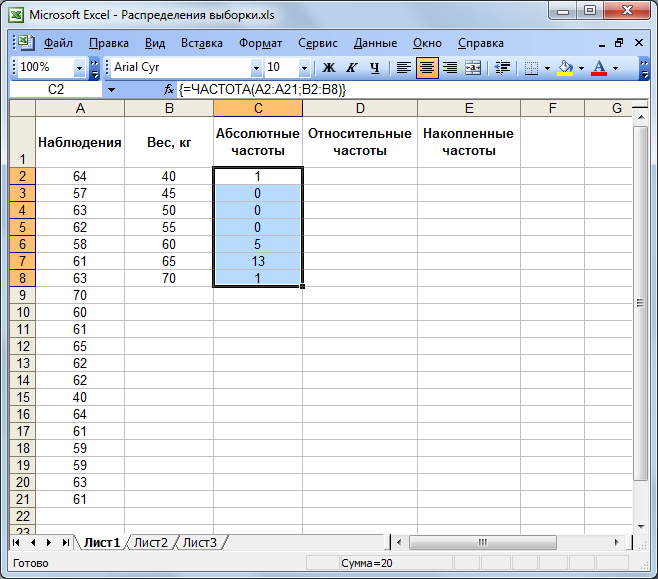
Рисунок 5.2 – Вигляд електронної таблиці після обчислення абсолютних частот

5. В комірці C9 знайдіть загальну кількість спостережень. Активізуйте осередок С9, на панелі інструментів Стандартна натисніть кнопку Автосума. Переконайтеся, що діапазон підсумовування зазначений правильно й натисніть клавішу Enter.

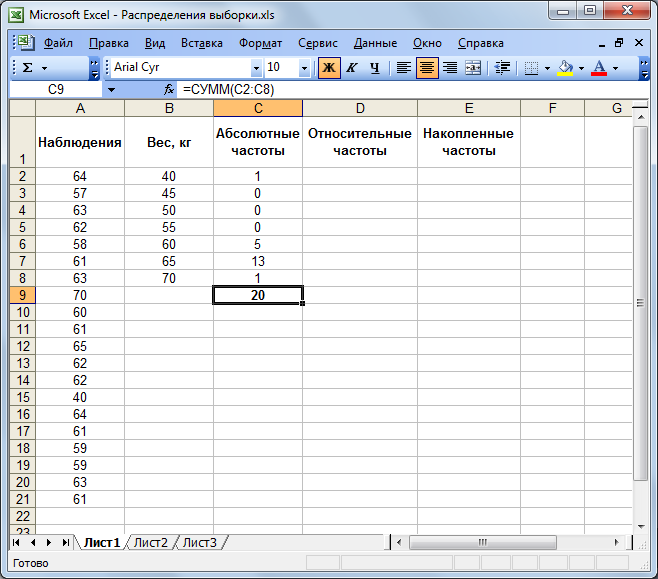
Рисунок 5.3 – Вигляд електронної таблиці після підсумовування

6. Заповніть стовпець відносних частот. В комірку введіть формулу для обчислення відносної частоти: =C2/$C$9. Натисніть клавішу Enter. Протяганням (за правий нижній кут при натиснутій лівій кнопці миші) скопіюйте уведену формулу в діапазон і одержіть масив відносних частот.

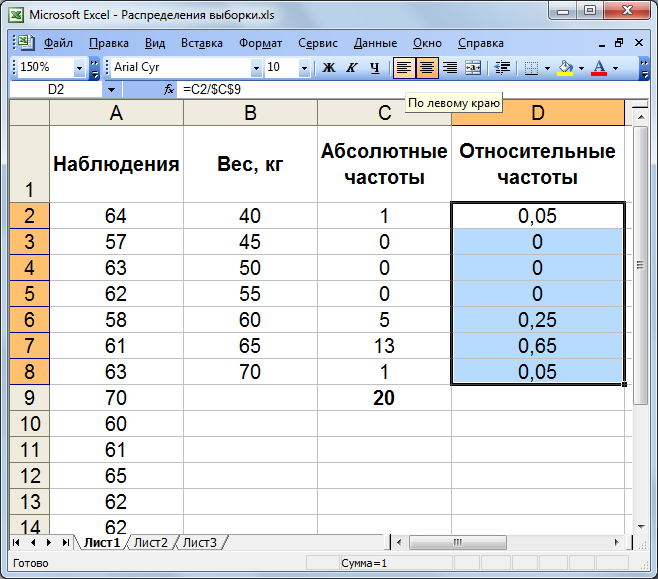
Рисунок 5.4 – Вигляд електронної таблиці після обчислення відносних частот

7. Заповніть стовпець накопичених частот. В комірку D2 скопіюйте значення відносної частоти з комірки E2. В комірку D3 уведіть формулу: =E2+D3. Натисніть клавішу Enter. Протяганням (за правий нижній кут при натиснутій лівій кнопці миші) скопіюйте уведену формулу в діапазон D3:D8. Одержимо масив накопичених частот.

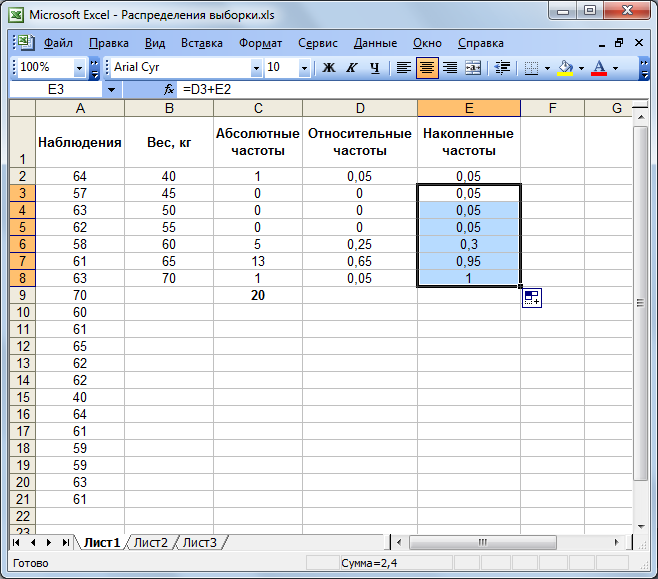
Рисунок 5.5 – Результат обчислень

8. Побудуйте діаграму відносних і накопичених частот. Клацанням курсору миші по кнопці на панелі інструментів викличте Майстер діаграм. У діалоговому вікні, що з'явилося, виберіть закладку Нестандартні й тип діаграми Графік/гістограма.

Завдання 2.

Для даних 64, 57, 63, 62, 58, 61, 63, 70, 60, 61, 65, 62, 62, 40, 64, 61, 59, 59, 63, 61.. (додайте самостійно до 55 штук) побудувати емпіричні розподіли, скориставшись процедурою Гістограма.

1. В комірку А1 уведіть слово Спостереження, а в діапазон А2:Е12 - дані.

2. Для виклику процедури Гістограма з меню Сервіс підпункт Аналіз даних; Інструменти аналізу - Гістограма.

3. У вікні, що з'явилося, Гістограма заповніть робочі поля :

   • У вхідний діапазон - (А2:Е12);

   • У вихідний діапазон посилання на ліву верхню комірку вихідного діапазону (F1). Встановіть перемикачі в положення Інтегральний відсоток і Вивід графіка. ОК.

Діаграма відрізняється від попереднього приклада. Поясніть чому.

Завдання для самостійної роботи.

1. Побудувати вибіркові функції розподілу (відносні й накопичені частоти) для росту в см. 20 студентів: 181, 169, 178, 178, 171, 179, 172, 181, 179, 168, 174, 167, 169, 171, 179, 181, 181, 183, 172, 176.

2. Знайдіть розподіл по абсолютних частотах для наступних результатів тестування в балах: 79, 85, 78, 85, 83, 81, 95, 88, 97, 85 (використовуйте границі інтервалів 70, 80, 90).