Контрольні питання

1. Що називають законом розподілу випадкової величини?

2. Що значить «біномінальний розподіл»?

3. Вивід біномінального розподілу, при яких умовах застосовується.

4. Чому дорівнює математичне очікування й дисперсія?

5. Куди зрушується максимум біномінального розподілу при великій кількості випробувань?

6. Привести приклади біномінального розподілу.

7. Які функції в MS Excel використовуються для роботи із цим розподілом.

Лабораторна робота № 4 «Побудова розподілів випадкових величин в ms Excel. Нормальний розподіл»

Мета роботи: навчитися використовувати нормальний розподіл для рішення задач теорії імовірності .

Завдання роботи:

- уміти знаходити імовірності безперервної випадкової величини, що підкоряється нормальному розподілу, за допомогою Excel;

- будувати діаграму нормального розподілу;

- уміти використовувати інтегральний розподіл.

Теоретичні відомості

Нормальний розподіл - це сукупність об'єктів, у якій крайні значення деякої ознаки — найменш і найбільше — з'являються рідко; чим ближче значення ознаки до математичного очікування, тим частіше воно зустрічається. Наприклад, розподіл студентів по їхній вазі наближається до нормального розподілу. Цей розподіл має дуже широке коло додатків у статистику, включаючи перевірку гіпотез.

Нормальний закон розподілу.

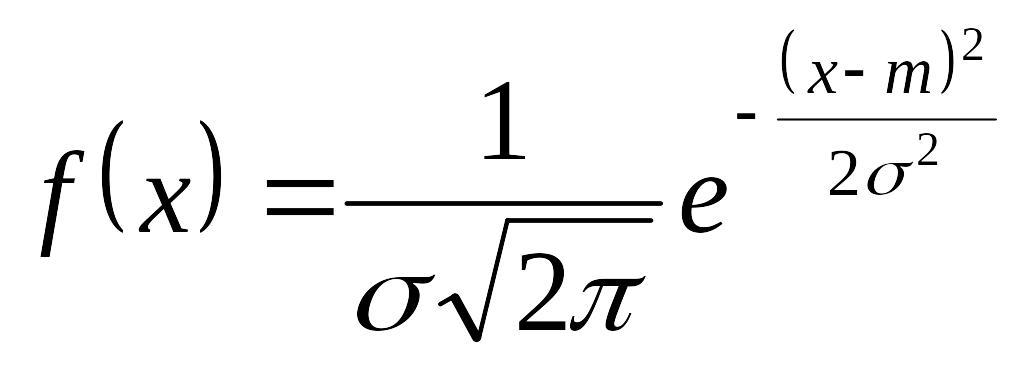, >0

При =1 і m=1 – нормальний стандартний розподіл ( m-мат. очікування, - дисперсія ). Діаграма нормального розподілу симетрична щодо точки m (математичного очікування). Медіана нормального розподілу дорівнює теж m. При цьому в точці m функція f(x) досягає свого максимуму.

В Excel для обчислення значень нормального розподілу використовується функція НОРМРАСП, що обчислює значення імовірності нормальної функції розподілу для зазначеного середнього й стандартного відхилення.

Функція має параметри:

НОРМРАСП (х; середнє; стандартне_відх; інтегральна), де:

х — значення вибірки, для яких будується розподіл;

середнє — середнє арифметичне вибірки;

стандартне_відх — стандартне відхилення розподілу;

інтегральний — логічне значення, що визначає форму функції. Якщо інтегральна має значення ІСТИНА(1), то функція НОРМРАСП повертає інтегральну функцію розподілу; якщо це аргумент має значення НЕПРАВДА (0), то обчислює значення функція щільності розподілу.

Якщо середнє = 0 і стандартне_відх = 1, то функція НОРМРАСП повертає стандартний нормальний розподіл.

Приклад 1. Побудувати графік нормальної функції розподілу f(x) при x, що міняється від 19,8 до 28,8 із кроком 0,5, математичним очікуванням 24,3 і стандартним відхиленням 1,5.

Рішення

1. В комірку А1 уводимо символ випадкової величини х, а в комірку B1 — символ функції щільності імовірності — f(x).

2. Уводимо в діапазон А2:А21 значення х від 19,8 до 28,8 із кроком 0,5. Для цього скористаємося маркером автозаповнення: в комірку А2 уводимо ліву границю діапазону (19,8), в осередок A3 ліву границю плюс крок (20,3). Виділяємо блок А2:А3. Потім за правий нижній кут простягаємо мишею до осередку А21 (при натиснутій лівій кнопці миші).

3. Установлюємо табличний курсор в осередок В2 і для одержання значення імовірності скористаємося спеціальною функцією — натискаємо на панелі інструментів кнопку Вставка функції (fx). У діалоговому вікні, що з'явилося, Майстер функцій - крок 1 з 2 ліворуч у поле Категорія зазначені види функцій. Вибираємо Статистична. Праворуч у поле Функція вибираємо функцію НОРМРАСП. Натискаємо на кнопку ОК.

4. З'являється діалогове вікно НОРМРАСП. У робоче поле X уводимо адресу осередку А2 клацанням миші на цьому осередку. У робоче поле Середнє вводимо із клавіатури значення математичного очікування (24,3). У робоче поле Стандартне_відх уводимо із клавіатури значення середньоквадратичного відхилення (1,5). У робоче поле Інтегральна вводимо із клавіатури вид функції розподілу (0). Натискаємо на кнопку ОК (рис 4.1).

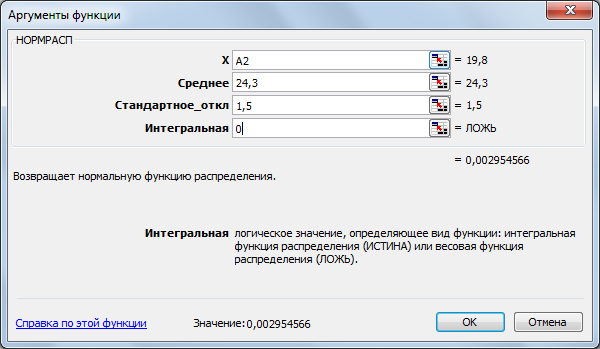
Рисунок 4.1 – Заповнені аргументи функції

5. В комірці В2 з'являється імовірність р = 0,002955. Курсором миші за правий нижній кут табличного курсору протяганням (при натиснутій лівій кнопці миші) з осередку В2 до В21 копіюємо функцію НОРМРАСП у діапазон В3:В21.

6. За отриманим даними будуємо шукану діаграму нормальної функції розподілу. Клацанням курсором миші на кнопці на панелі інструментів викликаємо Майстер діаграм. У діалоговому вікні, що з'явилося, вибираємо тип діаграми Графік, вид - лівий верхній. Після натискання кнопки Далі вказуємо діапазон даних — В1:В21 (за допомогою миші). Перевіряємо, положення перемикача Ряди в: стовпцях. Вибираємо закладку Ряд і за допомогою миші вводимо діапазон підписів осі X: А2:А21. Нажавши на кнопку Далі, уводимо назви осей Х и В і натискаємо на кнопку Готово.

Приклад 2. Побудувати діаграму стандартного нормального інтегрального розподілу.

1. В комірку А1 уводимо символ випадкової величини x, а в осередок В1 - символ стандартного нормального розподілу імовірності - Ф(x).

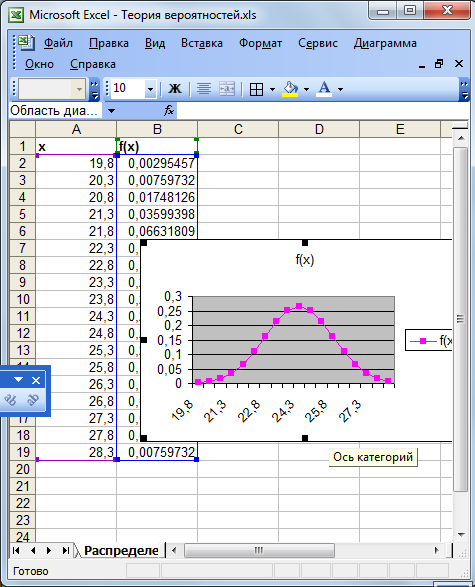
Рисунок 4.2 – Графік нормальної функції розподілу

2. Уводимо діапазон по x від -3 до 3 із кроком 0,5.

3. В В2 – вставка функції НОРМРАСПР. Розтягуємо В2 до В14.

4. Через майстер діаграм будуємо графік.

Приклад 3. Знайти верхню й нижню квартили для нормальної щільності при М=24,3 і дисперсії 2,25.

1. Для одержання значення верхньої квартили скористаємося спеціальною функцією НОРМОБР, що вставляємо в комірку А1.

2. У діалогове вікно, у робоче поле Імовірність уводимо значення імовірності верхньої квартили – 0,75, у Середнє – 24,3, у Стандартне_відх - середньоквадратичне відхилення ( у прикладі – 1.5). Після ОК в А1 з'являється значення верхньої квартили.

3. Повторюємо для осередку А2 (в Імовірність – 0.25).