Лабораторна робота №3 «Побудова розподілів випадкових величин в ms Excel. Біноміальний розподіл»

Мета роботи: навчитися використанню біноміального розподілу для рішення завдань теорії імовірності

Завдання роботи:

- уміти знаходити імовірності дискретної випадкової величини, що підкоряється біноміальному розподілу, за допомогою Excel;

- будувати діаграму біноміального розподілу;

- уміти використовувати інтегральний розподіл.

Теоретичні відомості

Розподіл імовірностей – одне з центральних понять теорії імовірності й математичної статистики. Визначення розподілу імовірності рівносильне завданню імовірностей всіх випадкових величин (ВВ), що описують деяку випадкову подію. Розподіл імовірностей деякої ВВ, можливі значення якої x₁,x₂, …x_n утворять вибірку, задається вказівкою цих значень і відповідних їм імовірностей p₁, p₂,… p_n (p_n повинні бути позитивні й у сумі давати одиницю).

У даній лабораторній роботі будуть розглянуті й побудовані за допомогою MS Excel найпоширеніший розподіл імовірності: біноміальний.

Біноміальний розподіл являє собою розподіл імовірностей числа настань деякої події («вдачі») в n повторних незалежних випробуваннях, якщо при кожному випробуванні імовірність настання цієї події дорівнює p. При цьому розподілі розкид варіант (є чи ні події) є наслідком впливу ряду незалежних і випадкових факторів.

Проводиться серія з n випробувань, у кожному з яких з імовірністю р може відбутися подія А, з імовірністю q= 1-р подія .

Імовірність настання події А не залежить від числа випробувань n і результатів інших випробувань.

Така схема випробувань із двома результатами (подія А настала або не настала) називається схемою послідовних випробувань Бернуллі.

Нехай при n випробуваннях подія А настала k раз, (n-k) раз подія .

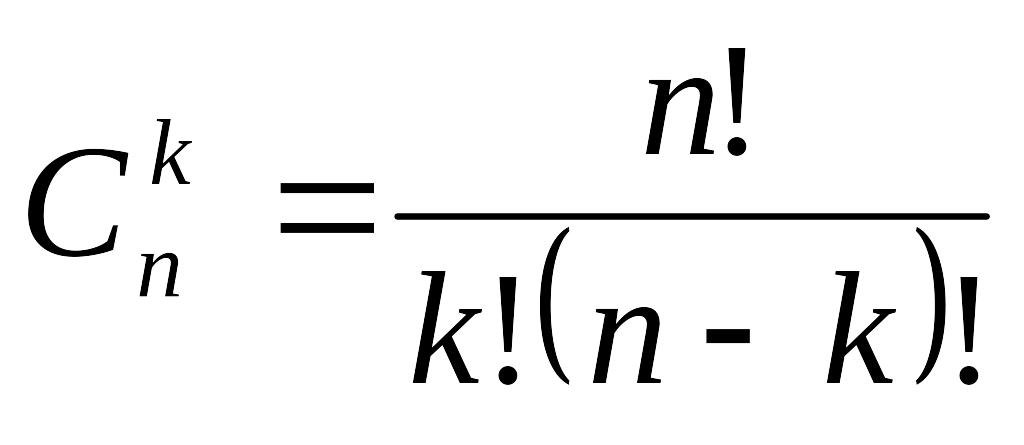
- число різних комбінацій події А.

Імовірність кожної окремої комбінації:

Імовірність того, що в серії з n випробувань подія А, імовірність якої дорівнює р, з'явиться k раз:

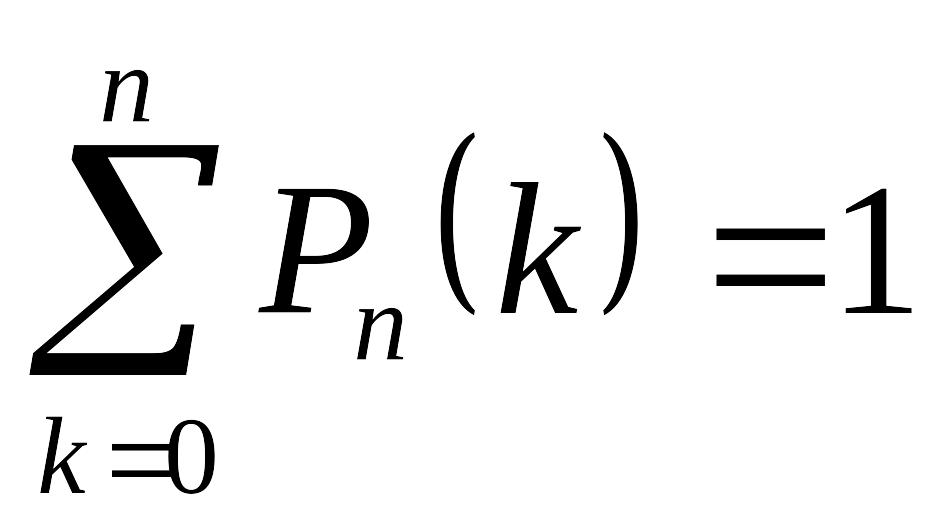- умова нормування.

Прикладом практичного використання біноміального розподілу може бути контроль якості партії фармакологічного препарату. Тут потрібно підрахувати число виробів (упакувань), що не відповідають вимогам. Всі причини, що впливають на якість препарату, приймаються однаково імовірними й не залежними другом від друга. Суцільна перевірка якості в цій ситуації неможлива, оскільки виріб, що пройшло випробування, не підлягає подальшому використанню. Тому для контролю з партії на удачу вибирають певну кількість зразків виробів (n). Ці зразки всебічне перевіряють і реєструють число бракованих виробів (k). Теоретично число бракованих виробів може бути від 0 до n.

В Excel функція БИНОМРАСП застосовується для обчислення імовірності в завданнях з фіксованим числом тестів або випробувань, коли результатом будь-якого випробування може бути тільки успіх або невдача.

Функція використовує наступні параметри:

БИНОМРАСП (число_успіхів; число_випробувань; імовірність_успіху; інтегральна)

число_успіхів — це кількість успішних випробувань;

число_випробувань — це число незалежних випробувань (число успіхів і число випробувань повинні бути цілими числами);

імовірність_ успіху — це імовірність успіху кожного випробування;

інтегральний — це логічне значення, що визначає форму функції.

Якщо даний параметр має значення ІСТИНА (=1), то вважається інтегральна функція розподілу (імовірність того, що число успішних випробувань не менш значення число_ успіхів);

якщо цей параметр має значення НЕПРАВДА (=0), то обчислюється значення функції щільності розподілу (імовірність того, що число успішних випробувань у точності дорівнює значенню аргументу число_ успіхів).

Приклад 1. Яка імовірність того, що троє із чотирьох немовлят будуть хлопчиками?

Рішення:

1. Установлюємо табличний курсор у вільну комірку, наприклад в А1. Тут повинне виявитися значення шуканої імовірності.

2. Для одержання значення імовірності скористаємося спеціальною функцією: натискаємо на панелі інструментів кнопку Вставка функції (fx).

3. У діалоговому вікні Майстер функцій - крок 1 з 2 ліворуч у полі Категорія зазначені види функцій. Вибираємо Статистична. Праворуч у полі Функція вибираємо функцію БИНОМРАСП і натискаємо на кнопку ОК.

З'являється діалогове вікно функції. У поле Число_успіхів уводимо із клавіатури кількість успішних випробувань (3). У поле Число випробувань уводимо із клавіатури загальну кількість випробувань (4). У робоче поле Імовірність_успіху вводимо із клавіатури імовірність успіху в окремому випробуванні (0,5). У поле Інтегральний уводимо із клавіатури вид функції розподілу — інтегральна або вагова (0). Натискаємо на кнопку ОК.

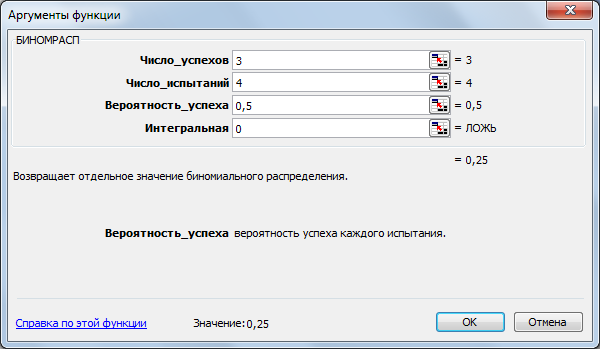
Рисунок 3.1 – Діалогове вікно уведення параметрів функції БИНОМРАСП

В комірці А1 з'являється шукане значення імовірності р = 0,25. Рівно 3 хлопчика з 4 немовлят можуть з'явитися з імовірністю 0,25.

Якщо змінити формулювання умови завдання й з'ясувати імовірність того, що з'явиться не більше трьох хлопчиків, то в цьому випадку в робоче поле Інтегральний уводимо 1 (вид функції розподілу інтегральний). Імовірність цієї події буде дорівнювати 0,9375.

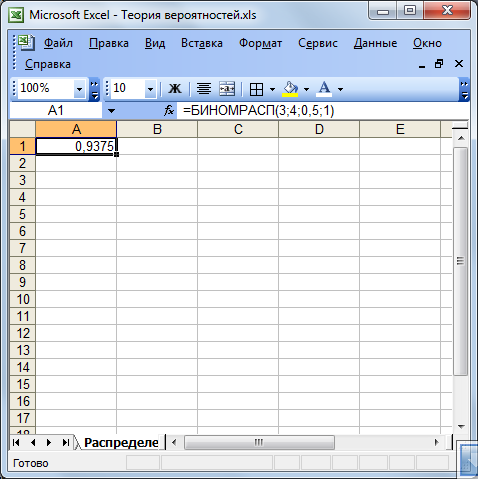
Рисунок 3.2 – Вигляд електронної таблиці після рішення завдання

Приклад 2. Побудувати діаграму біноміальної функції розподілу P(m) при n=10, P=0,2.

Рішення.

1. В комірку А1 уводимо символ кількості успішних ісходів, а в комірку В1 символ імовірності p.

2. Заповнюємо кількість ісходів в А1 - від 0 до 10.

3. В комірку В2 вставляємо, через «вставка функції» БИНОМРАСПР.

У робоче поле «число» уводимо кількість успішних випробувань (адреса комірки А2). В «випробування» - число випробувань (у нас – 10). В «імовірність» - 0,2. У робоче поле «Інтегральний» уводимо із клавіатури вид функції – у цьому випадку «0». В осередку В2 з'являється шукана імовірність, що «простягаємо» на весь діапазон.

4.Через «майстер діаграм» будуємо шукану діаграму біноміального розподілу, тип діаграми – гістограма.

Зберігаємо діаграму з відповідними написами на осях.

Приклад 3. В умовах попереднього приклада знайти значення числа m, для якого імовірність інтегрального розподілу дорівнює або більше 0,3.

1. Установлюємо табличний курсор у вільну комірку, наприклад в А1. Тут повинне виявитися значення шуканого числа m.

2. Для одержання значення імовірності скористаємося функцією КРИТБИНОМ.

3. У діалогове вікно вводимо: Випробування – 10, імовірність – 0,2. У робоче поле Альфа – критичне значення імовірності інтегрального розподілу (0,3).

4. В комірці А1 з'являється шукане значення числа успішних випробувань, у даному прикладі m=1.

Необхідно перевірити результат прямим розрахунком.

Завдання для самостійної роботи.

1. Яка імовірність того, що вісім з десяти студентів, що здають залік, одержать «незалік». (0,04)

2. При киданні монети може випасти орел або решка. Знайти імовірність того, що орел випаде в точності 6 разів з 10.

3. Побудувати діаграму біноміальної функції щільності імовірності при n=10, p=0.5.

4. Побудувати діаграму біноміальної інтегральної функції розподілу P(A<m) при n=10, p=0.2.

5. Вибірковий контроль продукції проводять так: з 100 вибирається 20 і при виявленні хоча б одного дефектного виробу вся партія бракується. У партії є 10 дефектних виробів. Яка імовірність того, що хоча б один дефектний виріб потрапить у вибірку?

6. Знайти кількість успішних випробувань для критичного значення інтегральної функції розподілу, рівного 0,75, якщо загальна кількість випробувань дорівнює 6, а імовірність успіху у випробуванні - 0,5.