Лабораторна робота № 2 «Визначення числових характеристик випадкової величини в ms Excel»
Мета роботи: навчитися обчислювати числові характеристики випадкової величини.
Завдання роботи:
- вміти знаходити математичне очікування дискретної випадкової величини за допомогою Excel;
- вміти знаходити дисперсію дискретної випадкової величини;
- вміти знаходити середньоквадратичне відхилення дискретної випадкової величини за допомогою Excel;
- вміти знаходити математичне очікування, дисперсію, моду, медіану, середньоквадратичне відхилення безперервної випадкової величини.
Теоретичні відомості
Дискретною називають випадкову величину, можливі значення якої є ізольовані числа, які ця величина приймає з певними імовірностями.
Законом
розподілу
дискретної випадкової величини
називають перелік її можливих значень
і відповідних
їм
імовірностей. Закон розподілу дискретної
випадкової величини
може бути заданий у вигляді таблиці,
перший рядок якої містить
можливі значення
,
а друга імовірності
:
|
|
|
|
|
|
|
|
|
|
де
.
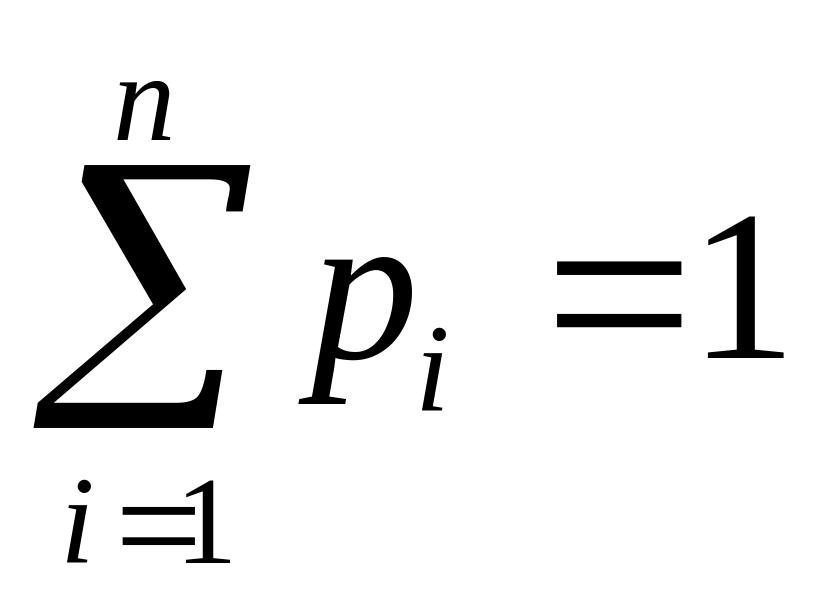Закон
розподілу дискретної випадкової величини
можна зобразити графічно, для чого
будують
прямокутну систему координат, причому
по осі абсцис відкладають можливі
значення
,
а по осі ординат – відповідні значення
імовірності
.
Будують
крапки
й з'єднують їхніми відрізками прямих.
Отриману фігуру називають багатокутником
розподілу.
Математичним очікуванням дискретної випадкової величини називають суму добутків всіх її можливих значень на їхній імовірності:
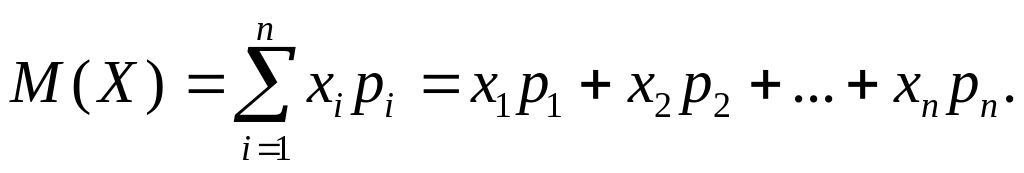
Математичне очікування служить характеристикою середнього значення випадкової величини.
Дисперсією випадкової величини називають математичне очікування квадрата відхилення:
Обчислювати дисперсію зручно по формулі:
Середнім квадратическим відхиленням випадкової величини називають квадратний корінь із дисперсії:
Дисперсія й середнє квадратическое відхилення служать характеристиками розсіювання можливих значень випадкової величини навколо математичного очікування.
Приклад.
Знайти математичне очікування
,
дисперсію
й середнє квадратическое відхилення
дискретної випадкової величини
,
закон розподілу якої заданий у вигляді
таблиці:
|
|
|
|
|
|
|
|
|
|
|
|
Рішення. Математичне очікування дорівнює сумі добутків всіх можливих значень на їхній імовірності:
.
Для обчислення дисперсії скористаємося формулою:
Складемо
закон розподілу
:
|
|
|
|
|
|
|
|
|
|
|
|
Знайдемо математичне очікування :
.
Підставивши
у формулу для обчислення дисперсії
та
знайдене
раніше, одержимо:
.
Знайдемо шукане середнє квадратическое відхилення:
.
Початковим
моментом порядку k
випадкової величини
називають математичне очікування
величини
:
.
Зокрема,
.
Центральним
моментом порядку k
випадкової величини
називають математичне очікування
величини
:
.
Зокрема,
.
Центральні моменти доцільно обчислювати, використовуючи формули, що виражають центральні моменти через початкові:
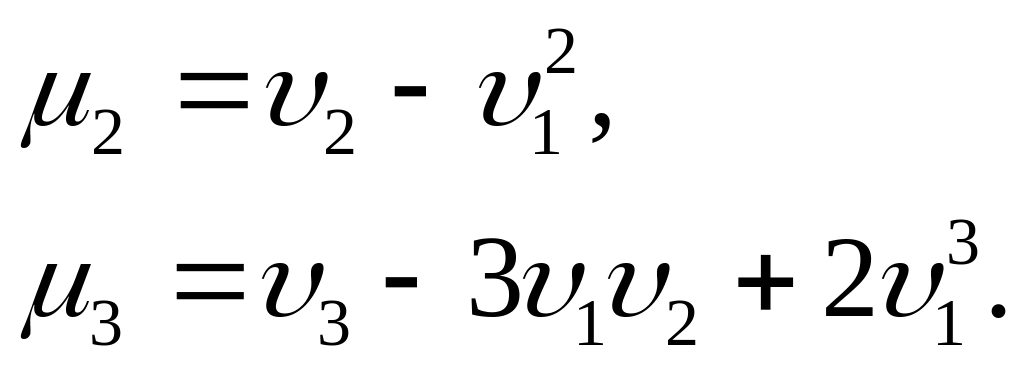
Приклад. Дискретна випадкова величина задана законом розподілу:
|
|
|
|
|
|
|
|
|
|
|
|
Знайти початкові й центральні моменти першого, другого та третього порядків.
Рішення. Знайдемо початковий момент першого порядку:
.
Складемо
закон розподілу величини
:
|
|
|
|
|
|
|
|
|
|
|
|
Знайдемо початковий момент другого порядку:
.
Складемо
закон розподілу величини
:
|
|
|
|
|
|
|
|
|
|
|
|
Знайдемо початковий момент третього порядку:
.
Центральний
момент першого порядку дорівнює нулю:
.
Для обчислення центральних моментів другого й третього порядків зручно скористатися формулами, що виражають центральні моменти через початкові:
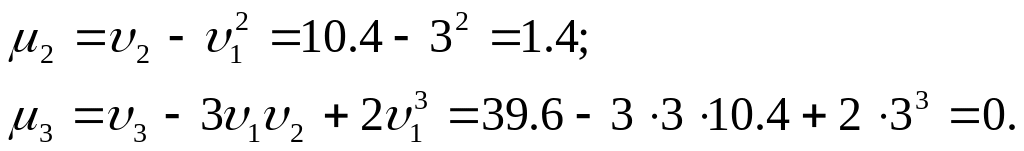
4. Загальний опис завдання
Лабораторна робота припускає попереднє вивчення, і засвоєння теоретичних положень. У роботі напрацьовуються навички обчислення математичного очікування, дисперсії, среднеквадратического відхилення випадкових величин. При рішенні завдань вивчаються різні властивості числових характеристик випадкових величин.
Для безперервних випадкових величин вивчаються поняття моди й медіани. При виконанні лабораторної роботи студент повинен вирішити завдання свого варіанта.
Завдання 1. Обчислення математичного очікування
Розглянемо знаходження математичного очікування для ряду дискретних значень. На рисунку 2.1 представлений ряд дискретних значень, причому в лівому стовпці представлені значення, а в правом – їхньої імовірності. Математичне очікування представленого ряду значень обчислюється по наступній формулі:
=СУММПРОИЗВ(A2:A11;B2:B11).
Результат обчислень математичного очікування поміщений в комірку В13.
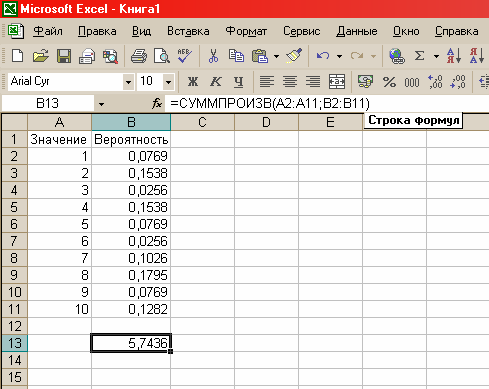
Рисунок 2.1 – Обчислення математичного очікування
Завдання 2. Обчислення дисперсії
Розглянемо приклад знаходження дисперсії випадкової величини. Знайдемо математичне очікування й зведемо його квадрат (рис. 2.2). Результат обчислень представлений осередку B13:
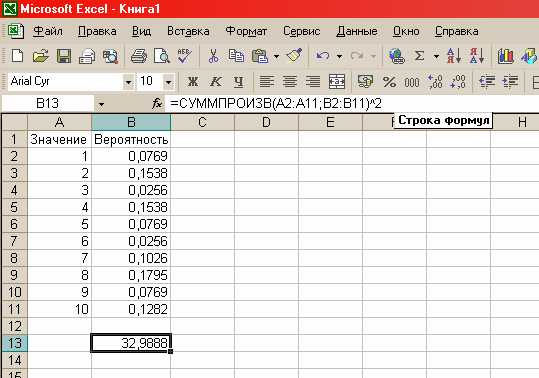
Рисунок 2.2 – Обчислення математичного очікування
Тепер знайдемо математичне очікування квадрата випадкової величини. Для цього зведемо випадкову величину у квадрат запишемо значення в стовпець С. Потім знайдемо математичне очікування для випадкової величини зі стовпця С. Результат обчислень представлений в комірці C13:
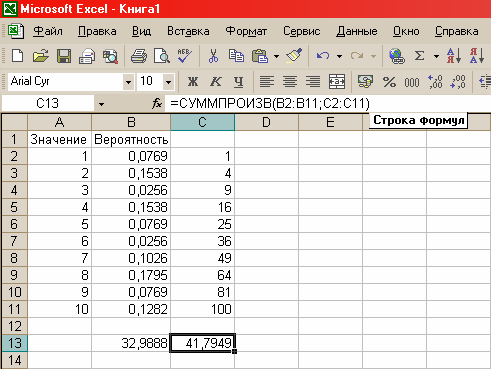
Рисунок 2.3 – Обчислення математичного очікування квадрата випадкової величини
Після цього залишається обчислити різницю між комірками С13 і В13, що й буде дисперсією випадкової величини Х.
Завдання 3. Обчислення середньоквадратичного відхилення випадкової величини
Після завершення роботи з попереднім завданням вам необхідно обчислити квадратний корінь зі знайденого значення дисперсії, що й буде середнім квадратичним відхиленням. В MS Excel квадратний корінь обчислюється з використанням функції КОРІНЬ(число). Помістіть результат в комірку В15.
Завдання для самостійної роботи.
1. Знайти математичне очікування, дисперсію й середнє квадратичне відхилення дискретної випадкової величини Х, заданої одним з наступних законів розподілу:
1.
-
Х
10
13
17
20
25
Р
0,4
0,3
0,1
0,15
0,05
2.
-
Х
8
14
17
20
23
Р
0,2
0,1
0,2
0,4
0,1
3.
-
Х
20
24
29
34
37
Р
0,2
0,3
0,25
0,15
0,1
4.
-
Х
14
15
17
25
26
Р
0,1
0,35
0,3
0,2
0,05
5.
-
Х
16
20
25
30
35
Р
0,2
0,15
0,15
0,3
0,2
6.
-
Х
0
1,5
1,9
2,5
2,9
Р
0,1
0,25
0,35
0,25
0,05
7.
-
Х
100
114
128
144
160
Р
0,2
0,35
0,2
0,15
0,1
8.
-
Х
45
53
67
80
95
Р
0,25
0,3
0,25
0,19
0,01
9.
-
Х
25
45
60
75
98
Р
0,15
0,25
0,3
0,2
0,1
10.
-
Х
60
75
80
105
110
Р
0,05
0,25
0,45
0,15
0,1
11.
-
Х
1
2
3
7
9
10
12
Р
0,04
0,26
0,31
0,09
0,18
0,11
0,01
12.
-
Х
6
8
14
17
19
20
23
Р
0,1
0,11
0,14
0,17
0,18
0,22
0,08
13.
-
Х
20
24
28
30
34
37
40
Р
0,1
0,23
0,25
0,18
0,13
0,08
0,03
14.
-
Х
10
13
15
17
25
27
29
Р
0,1
0,12
0,23
0,3
0,17
0,05
0,03
15.
-
Х
8
16
18
20
25
30
35
Р
0,01
0,17
0,19
0,26
0,15
0,12
0,1
16.
-
Х
0,5
1,5
1,9
2,3
2,5
2,9
3,2
Р
0,1
0,25
0,27
0,13
0,15
0,07
0,03
17.
-
Х
100
114
125
128
144
157
160
Р
0,1
0,25
0,23
0,17
0,15
0,08
0,02
18.
-
Х
45
53
61
67
78
80
95
Р
0,12
0,17
0,22
0,25
0,16
0,07
0,01
19.
-
Х
25
37
45
60
68
75
98
Р
0,015
0,085
0,125
0,17
0,3
0,2
0,1
20.
-
Х
60
75
77
80
105
108
110
Р
0,005
0,13
0,225
0,375
0,125
0,09
0,05
2. Дискретна випадкова величина приймає три можливих значення: х1=5 з імовірністю р1=0,5; х2=8 з імовірністю р2=0,3; х3 з імовірністю р3. Знайти значення величин х3 і р3, знаючи, що математичне очікування випадкової величини M ( X ) = 7.
3. Для кожного з варіантів завдання знайти математичне очікування, дисперсію і середнє квадратичне відхилення випадкової величини Z = 4X + 5Y, якщо відомі математичні очікування M(X) і M(Y) та дисперсії D(X) і D(Y) випадкових величин X і Y :
Завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
M ( X ) |
15 |
3,4 |
103 |
19 |
25 |
11 |
46 |
39 |
93 |
74 |
45 |
14 |
12 |
20 |
54 |
M (Y ) |
61 |
4,6 |
321 |
31 |
54 |
90 |
68 |
32 |
22 |
27 |
41 |
17 |
8 |
31 |
50 |
D( X ) |
0,02 |
7,1 |
32 |
2,4 |
6,8 |
0,2 |
8 |
3 |
4,1 |
0,8 |
5 |
4 |
2 |
0,3 |
5,8 |
D(Y ) |
0,04 |
1,2 |
46 |
1,1 |
7,7 |
0,4 |
2 |
4 |
3,3 |
0,1 |
3 |
8 |
6 |
0,1 |
8,7 |
4. Знайти математичне очікування, дисперсію й середнє квадратичне відхилення випадкової величини Z = 3X − 2Y, якщо відомі математичні очікування та дисперсії випадкових величин X та Y :
Завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
M ( X ) |
32 |
25 |
112 |
34 |
55 |
46 |
73 |
54 |
123 |
236 |
46 |
24 |
53 |
167 |
41 |
M (Y ) |
16 |
127 |
57 |
13 |
67 |
37 |
112 |
33 |
101 |
213 |
78 |
93 |
45 |
321 |
57 |
D( X ) |
4 |
12 |
42 |
23 |
3 |
2 |
11 |
14 |
13 |
17 |
5 |
11 |
3 |
34 |
3 |
D(Y ) |
6 |
19 |
12 |
40 |
4 |
6 |
21 |
15 |
17 |
6 |
8 |
9 |
6 |
67 |
5 |
5. Знайти математичне очікування, дисперсію й середнє квадратичне відхилення випадкової величини Z = 7X + 4Y, якщо відомі математичні очікування та дисперсії випадкових величин X та Y :
Завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
M ( X ) |
3,5 |
2,3 |
4,8 |
9,4 |
5,5 |
5 |
3,9 |
8,5 |
4,3 |
6,5 |
2,1 |
5,4 |
7,1 |
8,7 |
3 |
M (Y ) |
2,7 |
2,1 |
8,6 |
2,3 |
7,7 |
7 |
1,1 |
2,8 |
9,5 |
2,7 |
2,9 |
4,7 |
2,7 |
3,3 |
2 |
D( X ) |
0,1 |
0,4 |
0,2 |
1,1 |
0,3 |
1 |
2,1 |
1,4 |
1,3 |
0,4 |
0,1 |
0,6 |
0,3 |
0,6 |
1 |
D(Y ) |
0,5 |
0,3 |
0,9 |
1,9 |
0,2 |
5 |
3,5 |
0,5 |
1,8 |
0,6 |
0,5 |
0,5 |
1,5 |
1,3 |
5 |
6. Знайти математичне очікування, дисперсію й середнє квадратичне відхилення випадкової величини Z = 6X - 3Y, якщо відомі математичні очікування та дисперсії випадкових величин X та Y :
Завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
M ( X ) |
23 |
51 |
12 |
37 |
54 |
416 |
43 |
59 |
196 |
316 |
61 |
14 |
73 |
163 |
98 |
M (Y ) |
56 |
207 |
57 |
18 |
69 |
317 |
135 |
38 |
185 |
231 |
75 |
9 |
45 |
311 |
37 |
D( X ) |
3 |
21 |
42 |
29 |
7 |
4 |
27 |
31 |
28 |
25 |
6 |
11 |
3 |
34 |
8 |
D(Y ) |
7 |
17 |
12 |
42 |
2 |
3 |
33 |
56 |
57 |
63 |
3 |
5 |
7 |
55 |
4 |
7. Знайти математичне очікування, дисперсію й середнє квадратичне відхилення випадкової величини Z = 8X-5Y+4, якщо відомі математичні очікування та дисперсії випадкових величин X та Y :
Завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
M ( X ) |
54 |
31 |
12 |
82 |
54 |
168 |
43 |
59 |
106 |
116 |
81 |
14 |
33 |
113 |
68 |
M (Y ) |
87 |
17 |
57 |
18 |
69 |
217 |
135 |
38 |
185 |
231 |
55 |
79 |
45 |
311 |
47 |
D( X ) |
2 |
5 |
22 |
15 |
7 |
4 |
27 |
31 |
28 |
25 |
6 |
10 |
4 |
84 |
11 |
D(Y ) |
8 |
7 |
11 |
5 |
2 |
3 |
33 |
56 |
57 |
63 |
3 |
5 |
6 |
95 |
19 |
8. Знайти математичне очікування, дисперсію й середнє квадратичне відхилення випадкової величини Z = 4X-9Y+5, якщо відомі математичні очікування та дисперсії випадкових величин X та Y :
Завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
M ( X ) |
6,5 |
9,3 |
8,8 |
9,8 |
8,5 |
9 |
7,9 |
8,7 |
4,3 |
7,5 |
5,1 |
5,4 |
7,8 |
8,7 |
11 |
M (Y ) |
8,7 |
8,1 |
8,4 |
2,6 |
9,7 |
5 |
9,1 |
2,4 |
5,5 |
9,6 |
2,4 |
4,6 |
2,3 |
3,7 |
12 |
D( X ) |
0,5 |
0,9 |
0,3 |
1,4 |
1,3 |
3 |
1,1 |
1,2 |
0,3 |
0,6 |
0,8 |
0,2 |
0,9 |
0,6 |
3 |
D(Y ) |
0,4 |
0,5 |
0,3 |
1,2 |
2,2 |
4 |
4,5 |
0,3 |
0,8 |
0,2 |
0,5 |
0,7 |
1,3 |
1,8 |
8 |
9. Можливі значення дискретної випадкової величини x1 = 1; x2 = 2; x3 = 3, а математичні очікування цієї величини та її квадрата рівні відповідно: M (X) = 2, 3; M (X2) = 5, 9. Знайти закон розподілу цієї випадкової величини та її функцію розподілу.
Контрольні питання
1. Що таке математичне очікування випадкової величини? По якій формулі обчислюється дана характеристика?
2. Що таке дисперсія випадкової величини? По якій формулі обчислюється дана характеристика?
3. Що таке середньоквадратичне відхилення випадкової величини? По якій формулі обчислюється дана характеристика?