Хід виконання завдання

1. У раніше створеному файлі (при виконанні завдання 1) перейменувати «Аркуш 2» в «Комбінаторика».

2. Сполучення. Довільна k-елементна підмножина даної множини з n елементів називається сполученням з N елементів по k. Порядок елементів у сполученні не суттєвий. Приклад типового завдання на сполучення: є 2 червоних і 5 жовтих тюльпанів; букет складають із 3-х квіток; скільки різних варіантів складання букета? Тут береться підмножина з 3-х елементів із множини, що складається з 7-ми елементів, порядок зовсім не важливий.

3. Кількість сполучень можна обчислити за допомогою функції ЧИСЛОКОМБ(n;k), що відноситься до математичних функцій.

4. На відповідному аркуші введіть заголовок в комірку А1 («Сполучення»).

5. В комірку А2 введіть текст «Загальна кількість елементів», в комірку В2 - «Кількість елементів підмножини», в комірку С2 - «Кількість сполучень».

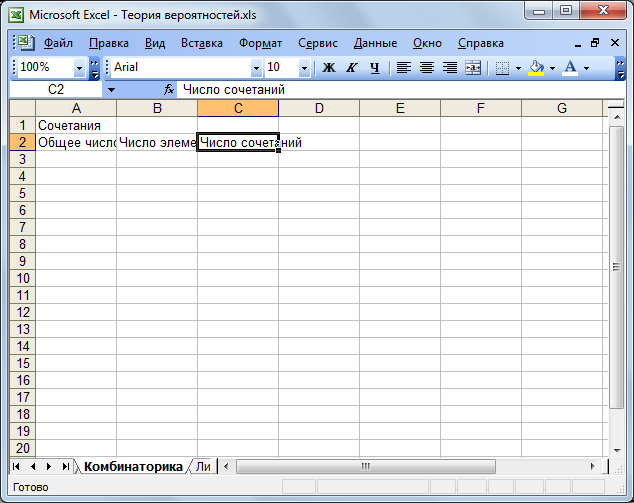
Рисунок 1.8 – Зовнішній вигляд аркуша електронної таблиці після введення заголовків

6. Об'єднайте комірки А1, В1 і С1. Для цього виділите відповідні комірки й виберіть пункт «Формат комірок» з меню «Формат», або з контекстного меню. У вікні, що відкрилося, активуйте пункт «Об'єднання комірок». Натисніть ОК.

7. Змініть формат комірок із заголовками відповідно до попереднього завдання.

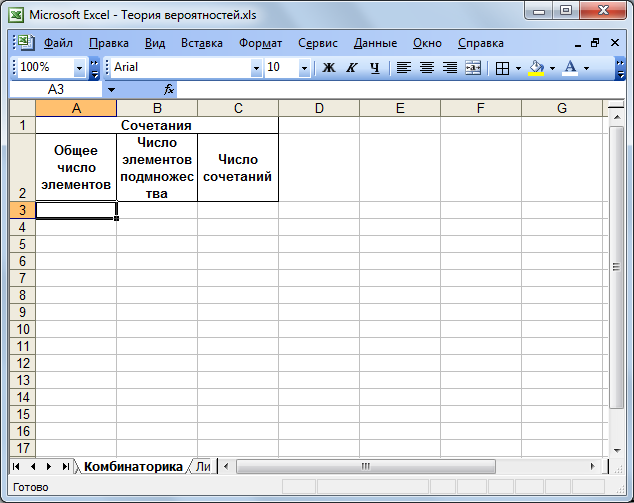
Рисунок 1.9 – Зовнішній вигляд таблиці після форматування заголовків

8. В комірку С3 введіть формулу для обчислення сполучень:

=ЧИСЛКОМБ(А3;В3)

Цю формулу ви можете ввести двома способами: або вручну, набравши її із клавіатури, або з використанням майстра функцій, піктограма для якого перебуває в рядку формул вікна електронної таблиці.

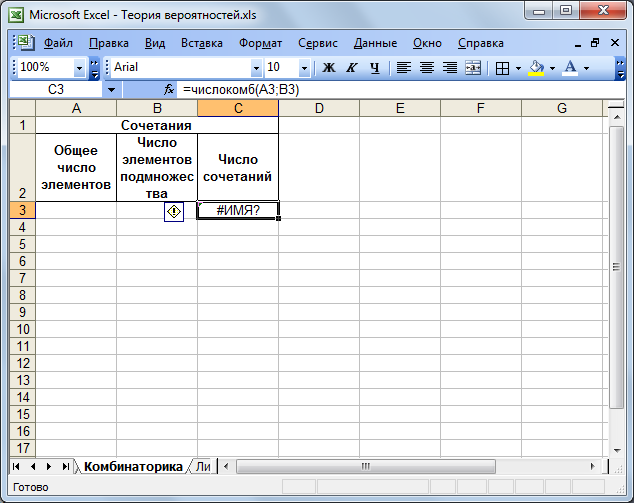
Рисунок 1.10 – Вигляд електронної таблиці після введення формули

9. Підставте значення, зазначені в прикладі вище, для обчислення кількості сполучень.

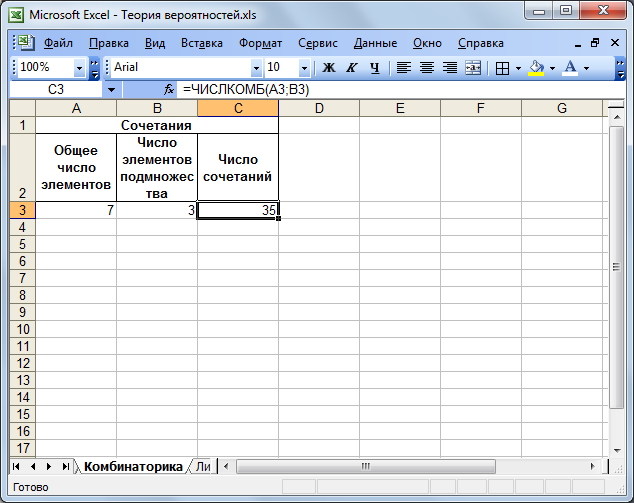
Рисунок 1.11 – Вигляд електронної таблиці після введення значень

10. Скопіюйте дану формулу на 10 рядків нижче.

Рисунок 1.12 – Вигляд електронної таблиці після копіювання формули

11. Розміщення. Різні впорядковані k-елементні підмножини множини з n елементів називаються розміщеннями з n елементів по k. Розміщення відрізняються один від одного або елементами, або їхніми порядками проходження. Приклад типового завдання на обчислення розміщень: у групі 5 дівчин і 8 юнаків. Для представництва цієї групи на конференції вибирають 4 людини, яким привласнюються номери для виступу на даній конференції. Скільки різних варіантів складання такої групи можна побудувати? У даному завданні буде мінятися як склад підмножини, так і порядок елементів даної підмножини. Тому застосовується формула для обчислення розміщень.

12. Обчислення розміщень засобами MS Excel можна реалізувати із застосуванням функції ПЕРЕСТ(n;k), де n– кількість елементів ісходної множини, а k – кількість елементів обраної підмножини.

13. Виділіть в аркуші «Комбінаторика» діапазон комірок А1:С2. Скопіюйте їхній зміст у буфер (або сполученням клавіш Ctrl+C, або Виправлення - Копіювати).

14. Встановіть курсив миші в комірку Е1. Вставте вміст буфера (сполучення клавіш Ctrl+V або Виправлення - Вставити).

15. Замініть текст комірки Е1 на «розміщення», а текст комірки G2 - на «Число розміщень».

16. До комірки G3 введіть функцію для обчислення розміщень.

17. Вирішіть задачу, зазначену як типову в даному завданні.

Рисунок 1.13 – Вигляд електронної таблиці після введення формули і значень із приклада

18. Скопіюйте формулу на 10 комірок вниз.

Рисунок 1.14 – Вигляд електронної таблиці після копіювання формули

19. Перестановки. Різні впорядковані множини, які відрізняються лише порядком елементів, тобто можуть бути отримані з тої ж самої множини перестановкою місцями елементів, називаються перестановками цієї множини. Приклад типового завдання на обчислення перестановок: скільки способів існує для того, щоб розставити 5 різних книг на книжковій полиці? Важливий порядок, кількість елементів зберігається, значить - перестановка. Це окремий випадок розміщень.

20. Обчислення перестановок можна виконати з використанням тої ж функції ПЕРЕСТ(n;n). Помітьте, що обидва параметри у цієї функції в цьому випадку будуть посилатися на ту саму комірку, тому що кількість елементів зберігається.

21. В осередок I1 введіть текст «Перестановки», об'єднайте її з коміркою J1.

22. В комірки I2 і J2 введіть текст «Кількість елементів» і «Кількість перестановок», відповідно.

23. Отформатуйте дані заголовки.

24. В комірку J3 введіть формулу для обчислення перестановок.

25. Розв’яжіть типове завдання, зазначене вище.

26. Скопіюйте формулу на 10 рядків нижче.

Рисунок 1.15 – Вигляд електронної таблиці після створення шаблона для обчислення перестановок

27. Самостійно з використанням цього шаблона вирішите наступні комбінаторні завдання (для обчислень можна використовувати вільні комірки, якщо явно в умові завдання не зазначена кількість елементів множини й обираної підмножини):

1. Скількома способами можуть вісім чоловік стати в чергу до театральної каси?

2. У магазині "Усе для чаю'' є 5 різних чашок і 3 різні блюдця. Скількома способами можна купити чашку із блюдцем?

3. В автомашині 7 місць. Скількома способами сім чоловік можуть сісти в цю машину, якщо зайняти місце водія можуть тільки троє з них?

4. Скільки слів можна утворити з букв слова фрагмент, якщо слова повинні складатися: (а) з восьми букв, (б) із семи букв, (в) із трьох букв?

5. Скільки існує різних автомобільних номерів, які складаються з п'яти цифр, а) якщо перша з них не дорівнює нулю; б) якщо номер складається з однієї букви латинського алфавіту, за котрою ідуть чотири цифри, відмінні від нуля?

6. Алфавіт деякої мови містить 30 букв. Скільки існує слів іх шести літер (ланцюжок букв від пробілу), складених з букв цього алфавіту, якщо: (а) літери в словах не повторюються? (б) букви в словах можуть повторюватися?

7. Скількома способами можна розставити на полці сім книг, якщо (а) дві певні книги повинні завжди стояти поруч,(б) ці дві книги не повинні стояти поруч?

8. Скількома способами з восьми чоловік можна обрати комісію, що складається з п'яти членів?

9. Скількома способами можна відібрати кілька фруктів із семи яблук, чотирьох лимонів і дев'яти апельсинів? (Ми вважаємо, що фрукти одного виду нерозрізнені.)

10. Скільки слів із 5 літер, кожне з яких складається із трьох приголосних і двох голосних, можна утворити з букв слова рівняння?

Контрольні питання

1. Яке програмне забезпечення (ПЗ) для роботи з електронними таблицями (ЕТ) вам відомо? Які основні функції виконує ПЗ для роботи з ЕТ?

2. Які адреси мають комірки ЕТ?

3. Яким чином можна додати формулу для обчислень в ЕТ? Де можна вводити формулу?

4. Як можна викликати попередньо встановлений список стандартних формул програми?

5. Які функції існують для обчислень максимуму й мінімуму в ЭТ?

6. Які функції існують для обчислення середнього значення в ЭТ?

7. Як здійснюється копіювання значень комірки в інші комірки?

8. Чим відрізняються абсолютна й відносна адресації комірок у формулах? Привести приклади використання.

9. Як знайти суму значень яких-небудь комірок?

10. Введіть формули (математичні, НЕ електронних таблиць) для обчислення сполучень, розміщень і перестановок з використанням засобу Equation у складі пакета MS Word. Поясніть значення даних формул.

11. Наведіть приклади, у яких використовуються формули на обчислення сполучень, розміщень і перестановок.

12. Що значить «правило добутку» у комбінаториці? Приведіть приклади.

13. Дайте класичне визначення імовірності.

14. Що таке умовна імовірність?

15. Для чого застосовується формула Байеса? Приведіть приклади.

16. Для чого застосовується формула Бернуллі? Приведіть приклади.

17. Що значить «повна імовірність»? Як її розрахувати?