
- •Для матрицы линейного оператора найти: а) собственные числа;
- •Решить типичные задачи:
- •§5. Векторная алгебра
- •1. Даны координаты вершин пирамиды , , и
- •§6. Комплексные числа
- •Решить уравнение: .
- •Найти алгебраическую форму комплексного числа
- •§7. Интегрирование
- •II. Вычислить интегралы:
- •II. Найти определенные интегралы:
- •§8. Дифференциальные уравнения
- •I. Решить дифференциальные уравнения и задачу Коши:
- •Решить типичные задачи:
- •II. Решить дифференциальные уравнения:
- •III. По виду правой части выписать вид частного решения
- •Экзаменационная программа.
Решить типичные задачи:
а).
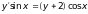 б).
б).
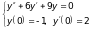
а).
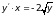 б).
б).
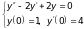
а).
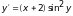 б).
б).

а).
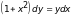 б).
б).
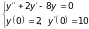
а).
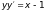 б).
б).

а).
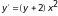 б).
б).
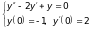
а).
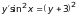 б).
б).
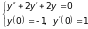
а).
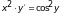 б).
б).
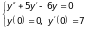
в).
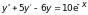 в).
в).
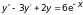
в).
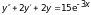 в).
в).

в).
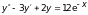 в).
в).
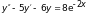
в).
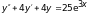 . в).
. в).
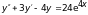
Примеры решения аналогичных задач есть в [1]: примеры 49.5, 50.1, 50.2, 51.4,51.2,51.3. и в [2], том 2: задачи 2.7.18, 2.7.25, 2.7.30 , 2.7.37, 2.7.43.
II. Решить дифференциальные уравнения:
1)
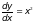 2)
2)

3)
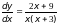 4)
4)
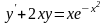
5)

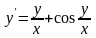 6),
6),
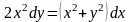
7)
 8)
8)
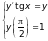 ,
,
9)
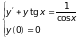 10)
10)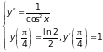
11)
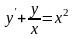 12)
12)
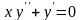
13)
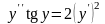 14)
14)
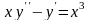
15)
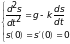 16)
16)
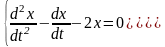
17)
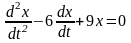 18)
18)
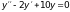
19)
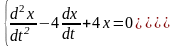 20)
20)
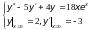
21)
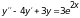 22)
22)
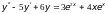
23)
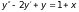 24)
24)
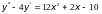
25)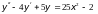 26)
26)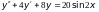
III. По виду правой части выписать вид частного решения
1)
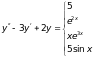 2)
2)
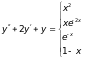
3)
 4)
4)
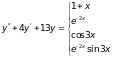
5)
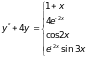 6)
6)
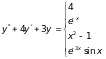
Экзаменационная программа.
Математический анализ.
Первообразная. Определение. Теорема о разности двух первообразных (доказательство, ее геометрический смысл).
Неопределенный интеграл. Определение. Основные свойства (формулировки, применение).
Таблица основных неопределенных интегралов. Интегрирование по таблице с помощью разложения подынтегрального выражения в алгебраическую сумму табличных слагаемых (на конкретных примерах).
Интегрирование подведением под знак дифференциала (проиллюстрировать метод на конкретных примерах).
Интегрирование по частям в неопределенном интеграле (вывод формулы, примеры ее применения).
Интегрирование рациональных дробей разложением на простейшие слагаемые: простейшие дроби 1-го и 2-ого и 3-ого типа. Метод неопределенных коэффициентов (на конкретных примерах).
Интегрирование выражений, содержащих квадратный трехчлен (на конкретных примерах).
Интегрирование некоторых тригонометрических выражений (на конкретных примерах).
Интегрирование некоторых иррациональных функций (на конкретных примерах).
Задачи, приводящие к понятию определенного интеграла: нахождение площади криволинейной трапеции, нахождение работы переменной силы.
Определенный интеграл как предел интегральных сумм. Геометрический смысл определенного интеграла. Условия существования определенного интеграла (без доказательства), определенный интеграл от кусочно-непрерывной функции.
Свойства определенного интеграла: линейность, аддитивность, изменение порядка интегрирования (формулировки свойств).
Интегрирование неравенства. Теорема об оценке определенного интеграла (геометрический смысл свойств, иллюстрация на конкретных примерах).
Теорема о среднем значении для определенного интеграла (доказательство, геометрический смысл).
Определенный интеграл с переменным верхним пределом. Теорема о производной интеграла по переменному верхнему пределу (формулировка).
Формула Ньютона - Лейбница (с доказательством).
Замена переменной в определенном интеграле (на конкретных примерах).
Интегрирование по частям в определенном интеграле (на конкретных примерах).
Полярная система координат. Переход из декартовой системы в полярную систему координат.
Вычисление площадей с помощью определенного интеграла в декартовой и полярной системах координат.
Объем тела вращения (формула, её применение при решении задач).
Понятие несобственного интеграла. Несобственные интегралы с бесконечными пределами (определение, примеры вычисления).
Дифференциальные уравнения, основные понятия, виды уравнений. Обыкновенные дифференциальные уравнения 1 порядка. Общее и частное решения. Задача Коши.
Дифференциальные уравнения с разделяющимися переменными (постановка задачи, ее решение на конкретных примерах).
Однородные дифференциальные уравнения 1-го порядка (постановка задачи, ее решение на конкретных примерах).
Линейные дифференциальные уравнения 1-го порядка. Однородные и неоднородные линейные уравнения. Теорема о структуре общего решения неоднородного линейного уравнения. Нахождение общего решения методом Лагранжа вариации произвольной постоянной (постановка задачи, ее решение на конкретных примерах).
Дифференциальные уравнения 2-го порядка. Основные понятия. Общее и частное решения. Задача Коши (ее геометрический смысл).
Линейные дифференциальные уравнения 2-го порядка. Линейная зависимость и независимость решений. Определитель Вронского. Структура общего решения линейного однородного дифференциального уравнения 2-го порядка (без доказательства).
Линейные неоднородные дифференциальные уравнения 2-го порядка. Структура общего решения линейного неоднородного дифференциального уравнения 2-го порядка (без доказательства).
Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Вывод формулы для общего решения в случае действительных различных корней характеристического уравнения (положительный дискриминант).
Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Вывод формулы для общего решения в случае действительных одинаковых корней характеристического уравнения (нулевой дискриминант).
Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Формула для общего решения в случае комплексно-сопряженных корней характеристического уравнения (отрицательный дискриминант, без вывода).
Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Нахождение общего решения методом Лагранжа вариации произвольных постоянных (постановка задачи, ее решение на конкретных примерах).
Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью вида f(x)= P(x)eax, где P(x)- многочлен. Нахождение общего решения методом неопределенных коэффициентов (постановка задачи, ее решение на конкретных примерах).
Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью вида f(x)=eax(Acoskx+Bsinkx). Нахождение общего решения методом неопределенных коэффициентов (постановка задачи, ее решение на конкретных примерах).
Векторная алгебра и аналитическая геометрия (в данном разделе требуется знание основных понятий, формул и умение применять их при решении практических задач)
Комплексные числа, действия над комплексными числами. Представление комплексного числа в алгебраической, тригонометрической и показательной формах. Возведение комплексного числа в степень и извлечения корня.
Геометрические векторы. Линейные комбинации векторов. Выполнение линейных операций над векторами, заданными координатами в стандартном базисе.
Скалярное произведение векторов. Вычисление скалярного произведения в стандартном базисе. Алгебраические свойства скалярного произведения их применение к решению задач.
Векторное произведение векторов. Вычисление векторного произведения в стандартном базисе. Алгебраические свойства векторного произведения их применение к решению задач.
Смешанное произведение векторов. Вычисление смешанного произведения в стандартном базисе. Алгебраические свойства смешанного произведения их применение к решению задач.
Плоскость в пространстве. Уравнение плоскости, заданной точкой и нормалью. Неполные уравнения плоскости и их геометрический смысл. Решение задач по теме.
Прямая в пространстве. Уравнения прямой, заданной точкой и направляющим вектором в двух формах (параметрической и канонической). Решение задач по теме.
Представление конечной системы векторов в виде матрицы. Понятие базисного минора матрицы. Нахождение ранга матрицы приведением ее к ступенчатому виду. Решение задач по теме.
Матрица линейного оператора. Собственные векторы и собственные значения линейного оператора, способ их нахождения. Характеристическое уравнение. Решение задач по теме.
Обращаю ваше внимание: то, что в программе НЕ подчеркнуто – в билет в явном виде не войдет. НО! Знать эти вопросы необходимо, чтобы решать задачи. Просто на письменном экзамене трудно удовлетворительно ответить на эти вопросы.
Итак, подчеркнуто – учи , студент.
Не подчеркнуто – читай внимательно и учись применять.
Обратите внимание на разобранные задачи. Если научитесь их решать, то с экзаменом проблем не будет.
Удачи!
