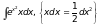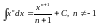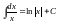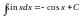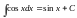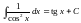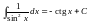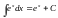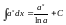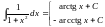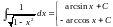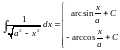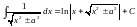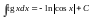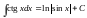- •Для матрицы линейного оператора найти: а) собственные числа;
- •Решить типичные задачи:
- •§5. Векторная алгебра
- •1. Даны координаты вершин пирамиды , , и
- •§6. Комплексные числа
- •Решить уравнение: .
- •Найти алгебраическую форму комплексного числа
- •§7. Интегрирование
- •II. Вычислить интегралы:
- •II. Найти определенные интегралы:
- •§8. Дифференциальные уравнения
- •I. Решить дифференциальные уравнения и задачу Коши:
- •Решить типичные задачи:
- •II. Решить дифференциальные уравнения:
- •III. По виду правой части выписать вид частного решения
- •Экзаменационная программа.
Для матрицы линейного оператора найти: а) собственные числа;
б) собственный вектор, соответствующий максимальному по абсолютной величине собственному числу; выполнить проверку.
Решение: Собственные числа
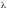 матрицы
матрицы
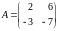 на-ходятся из условия равенства нулю
определителя
на-ходятся из условия равенства нулю
определителя
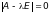 .
В нашем случае это
.
В нашем случае это
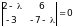 .
Раскрывая определитель, получаем
квадратное уравнение
.
Раскрывая определитель, получаем
квадратное уравнение
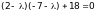 ,
имеющее вид
,
имеющее вид
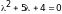 .
Собственные числа матрицы
.
Собственные числа матрицы
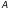 –
корни этого уравнения:
–
корни этого уравнения:
 .
.
Собственный вектор
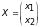 ,
отвечающий собственному числу
,
определяется равенством
,
отвечающий собственному числу
,
определяется равенством
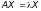 и находится из условия
и находится из условия
 .
В нашем случае это
.
В нашем случае это
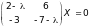 .
Так как
.
Так как

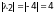 ,
то максимальным по абсолютной величине
собственным числом является
,
то максимальным по абсолютной величине
собственным числом является
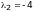 ,
тогда имеем
,
тогда имеем
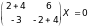 или
или
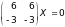 ,
что равносильно системе уравнений
,
что равносильно системе уравнений
 ,
из которой следует, что
,
из которой следует, что
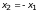 и вектор
и вектор
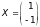 является собственным вектором для
является собственным вектором для
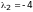 .
.
Проверка. Проверим, что
для
и собственного вектора
:
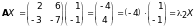 — верно.
— верно.
Решить типичные задачи:
Для матрицы линейного оператора найти:
a) собственные числа;
б) собственный вектор, соответствующий максимальному по абсолютной величине собственному числу; выполнить проверку.
1)
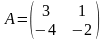 ,
2)
,
2)
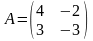 , 3)
, 3)
 ,
,
4)
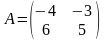 , 5)
, 5)
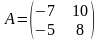 , 6)
, 6)
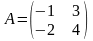 ,
,
7)
 , 8)
, 8)
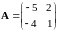 .
.
§5. Векторная алгебра
1. Даны координаты вершин пирамиды , , и
Найти:
а) длину ребра
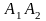 ;
;
б) угол между векторами
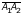 и
и
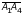 ;
;
в) площадь грани
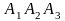 ;
;
г) объём пирамиды
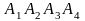 .
.
Решение: а) Найдем
координаты вектора
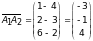 ,
тогда длина ребра
равна
,
тогда длина ребра
равна
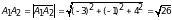 ;
;
б) Найдем координаты вектора
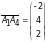 и его длину
и его длину
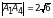
Из пункта а)
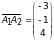 и
и
 ,
поэтому
,
поэтому

в)
Найдем координаты вектора
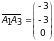 .
Тогда векторное произведение векторов
и
.
Тогда векторное произведение векторов
и
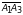 равно
равно
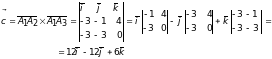
Площадь
грани равна половине длины полученного
вектора, то есть

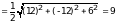 .
.
г)
Объём пирамиды
равен
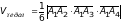 .
Находим смешанное произведение:
.
Находим смешанное произведение:
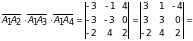
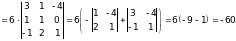 .
.
Здесь использовались свойства определителей. Можно было провести другое вычисление:
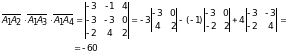 Окончательно
имеем
Окончательно
имеем
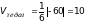 .
.
Решить типичные задачи:
Даны координаты вершин пирамиды
1)
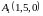 ,
,
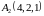 ,
,
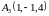 и
и
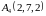 .
.
2)
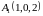 ,
,
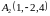 ,
,
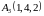 и
и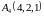 .
.
3)
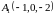 ,
,
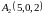 ,
,
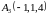 и
и
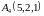 .
.
4)
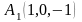 ,
,
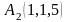 ,
,
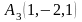 и
и
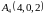 .
.
5)
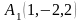 ,
,
 ,
,
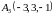 и
и
 .
.
6)
,
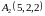 ,
,
 и
и
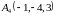 .
.
7)
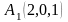 ,
,
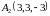 ,
,
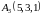 и
и
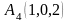 .
.
8)
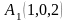 ,
,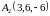 ,
,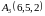 и
и
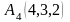 .
.
Найти: а) длину ребра ;
б) угол между векторами и ;
в) площадь грани ; г) объём пирамиды .
Аналогичные задачи с решениями есть в [2], том 1: задачи 3.1.13, 3.2.8 а), 3.3.5, см. также 3.4.4.
§6. Комплексные числа
Решить уравнение: .
Решение.

или

Здесь введено обозначение
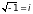 ,
тогда
,
тогда
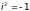 (величина i
называется мнимой единицей).
(величина i
называется мнимой единицей).
Решить типичные задачи:

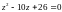
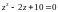
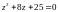
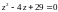
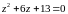
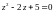
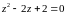
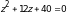
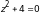
Найти алгебраическую форму комплексного числа
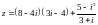 .
.
Решение.
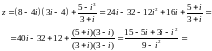
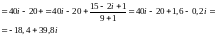
Пример решения аналогичной задачи есть в [1]: пример 28.2 (§28)
Решить типичные задачи:
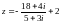
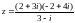
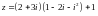
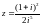
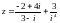
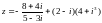
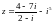
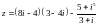
Аналогичная задача с решением есть в [2]: задача 10.2.1 и в [1]: примеры 20.11 (§20), 20.12 (§20), см. также 20.10 (§20) и 11.3.16
§7. Интегрирование
Таблица неопределенных интегралов:
Для того, чтобы научиться вычислять интегралы, надо выучить таблицу интегралов и освоить основные правила интегрирования. Одними из самых важных формул таблицы интегралов являются формулы
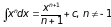 и
и
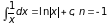
Для того, чтобы их хорошо запомнить, решите следующие задачи, предварительно ответив на вопросы:
“Чему равно
 ?”
и “Чему равно
?”
и “Чему равно
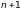 ?”
?”
1)
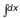 2)
2)
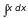 3)
3)
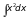 4)
4)
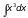
5)
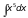 6)
6)
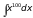 7)
7)
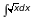 8)
8)
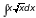
9)
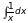 10)
10)
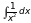 11)
11)
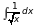 12)
12)
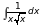
Добавьте в таблицу интегралов следующие формулы
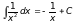 и
и
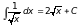
Заметим, что неопределенный интеграл обладает свойством линейности
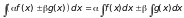
Примените это свойство к решению следующих задач:
1)
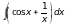 2)
2)
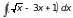 3)
3)
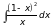
4)
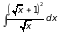 5)
5)
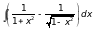 6)
6)
 .
.
Чтобы освоить метод подведения под знак дифференциала, решите следующие задачи
1)
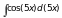 2)
2)
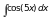 3)
3)

4)
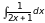 5)
5)
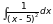 6)
6)
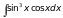
7)
 8)
8)
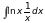 9)
9)