3. Рішення задач за допомогою електронних таблиць Excel

Рішення завдання можна спростити, використовуючи вбудовані функції. Активізуємо Мастер функций будь-яким із способів :

• у головному меню вибрати Вставка / Функция;

• на панелі інструментів Стандартная клацнути по кнопці Вставка функции.

Для обчислення вибіркових середніх використовуємо функцію СРЗНАЧ(число1: числоN) з категорії Статистические.

Вибіркова коваріація між та знаходиться за допомогою функції КОВАР(масив X;масив Y) з категорії Статистические.

Вибіркові дисперсії визначаються статистичною функцією ДИСПР(число1: числоN).

Вибірковий коефіцієнт кореляції між та обчислюється за допомогою статистичної функції КОРРЕЛ(масив X;масив Y).

Параметри лінійної регресії в Excel можна визначити декількома способами.

1 спосіб. За допомогою вбудованої функції ЛИНЕЙН. Порядок дій наступний:

1. Виділити область порожніх комірок 5×2 (5 рядків, 2 стовпці) для виведення результатів регресійної статистики або область 1×2 - для отримання тільки коефіцієнтів регресії.

2. За допомогою Мастера функций серед Статистических вибрати функцію ЛИНЕЙН і заповнити її аргументи (рис. 1.4):

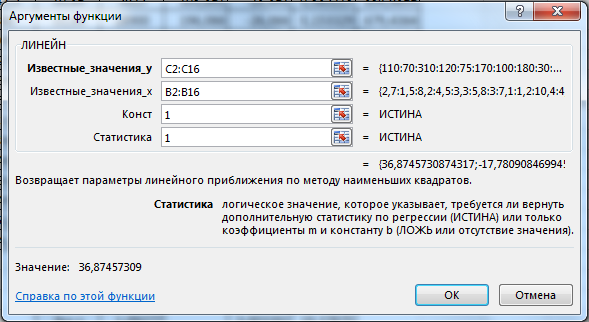
Рис. 1.4. Діалогове вікно введення аргументів функції ЛИНЕЙН

Известные_значения_y - діапазон, що містить дані результативної ознаки Y;

Известные_значения_x - діапазон, що містить дані пояснюючої ознаки X;

Конст - логічне значення (1 або 0), яке вказує на наявність або відсутність вільного члена в рівнянні; ставимо 1;

Статистика - логічне значення (1 або 0), яке вказує, виводити додаткову інформацію по регресійному аналізу або ні; ставимо 1.

3. У лівій верхній комірці виділеної області з'явиться перше число таблиці. Для розкриття усієї таблиці треба натиснути на клавішу <F2>, а потім - на комбінацію клавіш <CTRL> + <SHIFT> + <ENTER>.

Додаткова регресійна статистика буде виведена у виді (табл. 1.3):

Таблиця 1.3

Значення коефіцієнта	Значення коефіцієнта
Середньоквадратичне відхилення	Середньоквадратичне відхилення
Коефіцієнт детермінації	Середньоквадратичне відхилення
-статистика	Число ступенів свободи
Регресійна сума квадратів	Залишкова сума квадратів

В результаті застосування функції ЛИНЕЙН отримаємо:

36,87	-17,78
3,003	19,379
0,9206	35,606
150,74	13
191102,48	16480,9

2 спосіб. За допомогою інструменту аналізу даних Регрессия можна отримати результати регресійної статистики, дисперсійного аналізу, довірчі інтервали, залишки, графіки підбору ліній регресії, графіки залишків і нормальної ймовірності. Порядок дій наступний:

1. Необхідно перевірити доступ до Пакету анализа. Для цього в головному меню треба вибрати Сервис / Настройки і навпроти Пакета анализа встановити прапорець.

2. Вибрати в головному меню Сервис / Анализ данных / Регрессия і заповнити діалогове вікно (рис. 1.5):

Входной интервал Y - діапазон, що містить дані результативної ознаки Y;

Входной интервал X - діапазон, що містить дані пояснюючої ознаки X;

Метки - прапорець, який вказує, чи містить перший рядок назви стовпців або ні;

Константа-ноль - прапорець, що вказує на наявність або відсутність вільного члена в рівнянні;

Выходной интервал - досить вказати ліву верхню комірку майбутнього діапазону;

Новый рабочий лист - можна задати довільне ім'я нового листа, на який будуть виведені результати.

Для отримання інформації про залишки, графіків залишків, підбору і нормальної вірогідності треба встановити відповідні прапорці в діалоговому вікні. В результаті отримаємо підсумки як на рис. 1.6.

Рис. 1.5. Діалогове вікно введення параметрів інструменту Регрессии

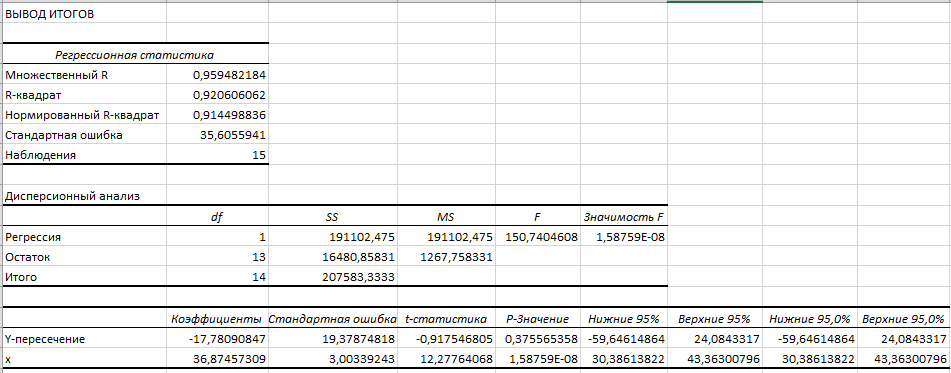
Рис. 1.6. Результати застосування інструменту Регрессии

У Excel лінія тренду може бути додана в діаграму з областями гістограми або в графік. Для цього:

1. Необхідно виділити область побудови діаграми і в головному меню вибрати Диаграмма / Добавить линию тренда.

2. У діалоговому вікні (рис. 1.7), що з'явилося, вибрати вид лінії тренду і задати відповідні параметри.

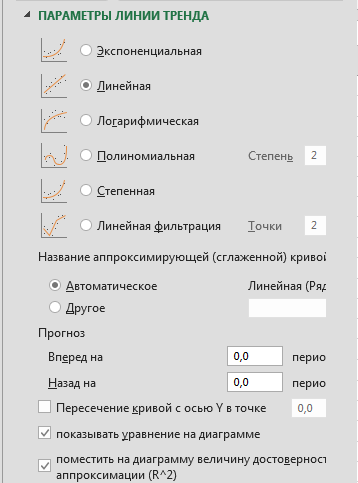
Рис. 1.7. Діалогове вікно параметрів лінії тренду

Для поліноміального тренду необхідно задати міру апроксимуючого полінома, для лінійної фільтрації - кількість точок усереднювання.

Вибираємо Линейная для побудови рівняння лінійної регресії.

В якості додаткової інформації можна показати рівняння на діаграмі і помістити на діаграму величину встановивши відповідні прапорці на закладці Параметры линии тренда (рис. 1.7).

В результаті отримаємо лінійний тренд (рис. 1.8).

Рис. 1.8. Лінійний тренд

Нелінійні моделі регресії ілюструються при обчисленні параметрів рівняння із застосуванням вибраної в Excel статистичної функції ЛГРФПРИБЛ. Порядок обчислень аналогічний застосуванню функції ЛИНЕЙН.

Початкові дані:

За даними 20 підприємств вивчається залежність випуску продукції на одного робітника Y (тис. грн.) від введення у дію основних фондів Х1 (% від вартості фондів на кінець року) і від питомої ваги робочих високої кваліфікації загальною кількістю працівників Х2 (%). Вхідні дані взяти згідно вашого варіанту.

Необхідно:

1. Побудувати лінійну модель множинної регресії. Записати стандартизоване рівняння множинної регресії. На основі стандартизованих коефіцієнтів регресії і середніх коефіцієнтів еластичності ранжирувати фактори за ступенем їх впливу на результат.

2. Знайти коефіцієнти парної, частинної та множинної кореляції. Проаналізувати їх.

3. Знайти скоригований коефіцієнт множинної детермінації. Порівняти його з нескоригованим (загальним) коефіцієнтом детермінації.

4. За допомогою - критерію Фішера оцінити статистичну значимість рівняння регресії та коефіцієнта детермінації .

5. За допомогою часткових -критеріїв Фішера оцінити доцільність включення у рівняння множинної регресії фактору після фактора і фактору після .

6. Скласти рівняння парної лінійної регресії, обравши тільки один значущій чинник.