- •Національний університет "Львівська політехніка"
- •Побудова та дослідження моделі множинної
- •Лінійної регресії з використанням засобів ms excel
- •Методичні вказівки до практичних занять з дисципліни
- •«Проектування технологічних процесів виготовлення електронних засобів»
- •I. Модель парної регресії
- •1. Основні визначення і формули
- •2. Рішення типових задач
- •3. Рішення задач за допомогою електронних таблиць Excel
- •Варіанти індивідуальних завдань
- •Список рекомендованої літератури
- •Значення критерію Стьюдента при
- •Значення критерію Фішера при
- •Методичні вказівки до практичних занять з дисципліни «Проектування технологічних процесів виготовлення електронних засобів»
- •Редактор
Міністерство освіти та науки України
Національний університет "Львівська політехніка"

Побудова та дослідження моделі множинної
Лінійної регресії з використанням засобів ms excel
Методичні вказівки до практичних занять з дисципліни
«Проектування технологічних процесів виготовлення електронних засобів»
для студентів спеціальностей 7/8.05090201, «Радіоелектронні апарати і засоби»
Затверджено
на засіданні кафедри "Електронні засоби інформаційно - комп’ютерних технологій"
Протокол ____ від ___________2014 р.
Львів 2014
Побудова та дослідження моделі множинної лінійної регресії з використанням засобів MS EXCEL. Методичні вказівки до практичних занять з дисципліни «Проектування технологічних процесів виготовлення електронних засобів» для студентів спеціальностей 7.05090201, 8.05090201 «Радіоелектронні апарати і засоби» / Укл. І.В.Атаманова. - Львів: НУ "ЛП", 2014. - 24 с.
Укладачі І.В. Атаманова, к.т.н., доц.
Відповідальний за випуск Т.А. Смердова, к.т.н., доц.
Рецензент Сторчун Є.В., д.т.н., проф.
Мета роботи - набути навичок побудови множинної лінійної регресії, оцінки її параметрів методом найменших квадратів (МНК). Дослідження моделі.
I. Модель парної регресії
1. Основні визначення і формули
Парна
регресія -
регресія (зв'язок) між двома змінними
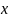 та
та
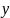 тобто модель виду:
тобто модель виду:
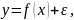
де - залежна змінна (результативна ознака);
– незалежна пояснююча змінна (ознака - фактор);
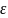 – збурення
або стохастична змінна, що включає вплив
неврахованих в моделі факторів.
– збурення
або стохастична змінна, що включає вплив
неврахованих в моделі факторів.
Практично
у кожному окремому випадку величина
складається з двох доданків:
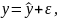
де - фактичне значення результативної ознаки;
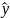 – теоретичне
значення результативної ознаки, знайдене
виходячи з рівняння регресії. Знак «^»
означає, що між змінними
та
немає строгої функціональної залежності.
– теоретичне
значення результативної ознаки, знайдене
виходячи з рівняння регресії. Знак «^»
означає, що між змінними
та
немає строгої функціональної залежності.
Розрізняють лінійні і нелінійні регресії.
Лінійна
регресія описується
рівнянням прямої
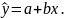
Нелінійні регресії діляться на два класи:
1) регресії, нелінійні по пояснюючих змінних, але лінійні за оцінюваними параметрами, наприклад:
• поліноми
різних ступенів
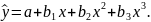
• рівностороння
гіпербола
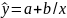
2) регресії, нелінійні за оцінюваними параметрами, наприклад:
• степенева
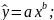
• показова
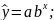
• експоненціальна
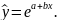
Для
побудови парної лінійної регресії
обчислюють допоміжні величини (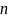 - число спостережень).
- число спостережень).
Вибіркові середні:
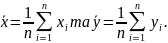
Вибіркова коваріація між та :
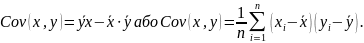
Коваріація - це числова характеристика спільного розподілу двох випадкових величин.
Вибіркова дисперсія для :
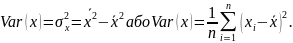
Вибіркова дисперсія для :
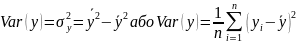
Вибіркова дисперсія характеризує ступінь розкиду значень випадкової величини навколо середнього значення (варіабельність, мінливість).
Тісноту зв'язку явищ, що вивчаються, оцінює вибірковий коефіцієнт кореляції між та :
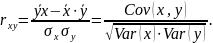
Коефіцієнт кореляції змінюється в межах від - 1 до +1. Чим ближче він по модулю до 1, тим ближче статистична залежність між та до лінійної функціональної.
Якщо
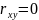 ,
то лінійний зв'язок між
та
відсутній;
,
то лінійний зв'язок між
та
відсутній;
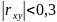 - зв'язок слабкий;
- зв'язок слабкий;
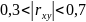 - зв'язок помірний;
- зв'язок помірний;
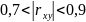 - зв'язок
сильний;
- зв'язок
сильний;
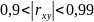 - зв'язок
дуже сильний.
- зв'язок
дуже сильний.
Додатне значення коефіцієнта свідчить про те, то зв'язок між ознаками прямий (із зростанням зростає значення ), від’ємне значення - зв'язок зворотний (із зростанням значення зменшується).
Побудова
лінійної регресії
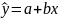 зводиться до оцінки її параметрів
зводиться до оцінки її параметрів
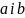 .
Класичний підхід до
оцінювання параметрів лінійної регресії
заснований на методі найменших квадратів
(МНК). МНК дозволяє отримати такі оцінки
параметрів, при яких сума квадратів
відхилень фактичних значень результативної
ознаки
від теоретичних
мінімальна, тобто
.
Класичний підхід до
оцінювання параметрів лінійної регресії
заснований на методі найменших квадратів
(МНК). МНК дозволяє отримати такі оцінки
параметрів, при яких сума квадратів
відхилень фактичних значень результативної
ознаки
від теоретичних
мінімальна, тобто
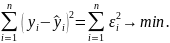
Для лінійної регресії параметри знаходяться з системи нормальних рівнянь:
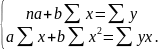
Вирішуючи систему, знаходимо вибірковий коефіцієнт лінійної регресії на :
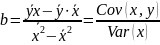
і параметр
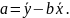
Коефіцієнт
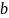 при факторній змінній
показує, наскільки зміниться в середньому
величина
при зміні фактора
на одиницю виміру.
при факторній змінній
показує, наскільки зміниться в середньому
величина
при зміні фактора
на одиницю виміру.
Параметр
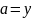 ,
коли
,
коли
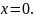 Якщо
не може дорівнювати 0, то
Якщо
не може дорівнювати 0, то
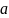 не має економічного сенсу. Інтерпретувати
можна тільки знак при
:
якщо
не має економічного сенсу. Інтерпретувати
можна тільки знак при
:
якщо
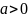 ,
та відносна зміна результату відбувається
повільніше, ніж зміна фактора, тобто
варіація результату менше варіації
фактора і навпаки.
,
та відносна зміна результату відбувається
повільніше, ніж зміна фактора, тобто
варіація результату менше варіації
фактора і навпаки.
Для оцінки якості побудованої моделі регресії можна використати коефіцієнт детермінації або середню похибку апроксимації.
Коефіцієнт детермінації
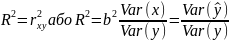
показує
долю дисперсії, що пояснюється регресією,
в загальній дисперсії результативної
ознаки
.
Відповідно, величина
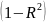 характеризує долю дисперсії показника
,
викликану впливом неврахованих в моделі
факторів та інших причин.
характеризує долю дисперсії показника
,
викликану впливом неврахованих в моделі
факторів та інших причин.
Чим
ближче
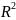 до 1, тим якісніше регресійна модель,
тобто побудована модель добре апроксимує
початкові дані.
до 1, тим якісніше регресійна модель,
тобто побудована модель добре апроксимує
початкові дані.
Середня помилка апроксимації - це середнє відносне відхилення теоретичних значень від фактичних , тобто
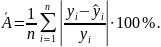
Побудоване
рівняння регресії вважається задовільним,
якщо значення
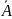 не перевищує 10-12%.
не перевищує 10-12%.
Для лінійної регресії середній коефіцієнт еластичності знаходиться по формулі:
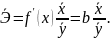
Середній коефіцієнт еластичності показує на скільки відсотків в середньому по сукупності зміниться результат від своєї величини при зміні фактора на 1% від свого значення.
Оцінка
значимості рівняння регресії в
цілому надається за допомогою
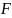 -критерия
Фишера, який полягає в перевірці гіпотези
про статистичну незначимість рівняння
регресії. Для цього виконується порівняння
фактичного
-критерия
Фишера, який полягає в перевірці гіпотези
про статистичну незначимість рівняння
регресії. Для цього виконується порівняння
фактичного
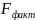 та критичного
(табличного)
та критичного
(табличного)
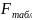 значень
-критерия
Фишера.
значень
-критерия
Фишера.
визначається із співвідношення значень факторної і залишкової дисперсії, розрахованих на один ступінь свободи, тобто
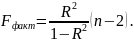
 – максимально
можливе значення критерію під впливом
випадкових факторів при ступенях свободи
– максимально
можливе значення критерію під впливом
випадкових факторів при ступенях свободи
 ,
і рівні значимості
,
і рівні значимості
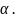 знаходиться з таблиці
-критерия
Фишера (табл. 1 додатку).
знаходиться з таблиці
-критерия
Фишера (табл. 1 додатку).
Рівень
значимості
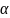 - це ймовірність відкинути правильну
гіпотезу за умови, що вона вірна.
- це ймовірність відкинути правильну
гіпотезу за умови, що вона вірна.
Якщо
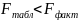 ,
то гіпотеза про відсутність зв'язку
показника, що вивчається, з фактором
відхиляється і робиться висновок про
суттєвість цього зв'язку з рівнем
значимості
(тобто рівняння регресії значиме).
,
то гіпотеза про відсутність зв'язку
показника, що вивчається, з фактором
відхиляється і робиться висновок про
суттєвість цього зв'язку з рівнем
значимості
(тобто рівняння регресії значиме).
Якщо
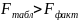 ,
то гіпотеза приймається і признається
статистична незначимість і ненадійність
рівняння регресії.
,
то гіпотеза приймається і признається
статистична незначимість і ненадійність
рівняння регресії.
Для
лінійної регресії значимість
коефіцієнтів регресії
оцінюють за допомогою
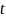 –критерія Стьюдента, згідно з яким
висувається гіпотеза про випадкову
природу показників, тобто про незначну
їх відмінності від нуля. Далі розраховуються
фактичні значення критерію для кожного
з оцінюваних коефіцієнтів регресії,
тобто
–критерія Стьюдента, згідно з яким
висувається гіпотеза про випадкову
природу показників, тобто про незначну
їх відмінності від нуля. Далі розраховуються
фактичні значення критерію для кожного
з оцінюваних коефіцієнтів регресії,
тобто
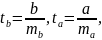
де
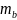 і
і
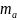 - стандартні похибки
параметрів лінійної регресії визначаються
за формулами:
- стандартні похибки
параметрів лінійної регресії визначаються
за формулами:
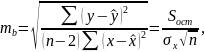
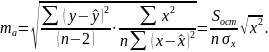
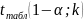 -
максимально можливе
значення критерію Стьюдента під впливом
випадкових факторів при даному ступені
свободи
-
максимально можливе
значення критерію Стьюдента під впливом
випадкових факторів при даному ступені
свободи
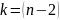 і рівні значимості
знаходиться з таблиці критерію Стьюдента
(табл. 2 додатку).
і рівні значимості
знаходиться з таблиці критерію Стьюдента
(табл. 2 додатку).
Якщо
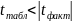 ,
то гіпотеза про
несуттєвість коефіцієнта регресії
відхиляється з рівнем значимості
,
тобто коефіцієнт (
або
)
не випадково відрізняється від нуля і
сформувався під впливом систематично
діючого фактора
.
,
то гіпотеза про
несуттєвість коефіцієнта регресії
відхиляється з рівнем значимості
,
тобто коефіцієнт (
або
)
не випадково відрізняється від нуля і
сформувався під впливом систематично
діючого фактора
.
Якщо
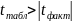 ,
то гіпотеза не відхиляється
і визнається випадкова природа формування
параметра.
,
то гіпотеза не відхиляється
і визнається випадкова природа формування
параметра.
Значимість лінійного коефіцієнта кореляції також перевіряється за допомогою – критерія Стьюдента, тобто
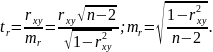
Гіпотеза
про несуттєвість коефіцієнта кореляції
відхиляється з рівнем значимість
,
якщо
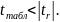
Зауваження.
Для лінійної парної регресії перевірки
гіпотез про значимість
коефіцієнта
і коефіцієнта кореляції
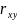 рівносильні перевірці гіпотези про
суттєвість рівняння регресії в цілому,
тобто,
рівносильні перевірці гіпотези про
суттєвість рівняння регресії в цілому,
тобто,
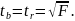
Для
розрахунку довірчого інтервалу визначають
граничну похибку для кожного показника,
тобто,
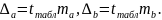
Довірчі інтервали для коефіцієнтів лінійної регресії:
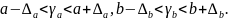
Якщо в межі довірчого інтервалу потрапляє нуль, тобто нижня межа від’ємна, а верхня додатна, то оцінюваний параметр приймається нульовим, оскільки він не може одночасно набувати і додатне і від’ємне значення.
Прогнозоване
значення
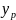 визначається шляхом
підстановки в рівняння регресії
відповідного прогнозного значення
визначається шляхом
підстановки в рівняння регресії
відповідного прогнозного значення
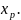 Потім обчислюється
середня стандартна
похибка прогнозу
Потім обчислюється
середня стандартна
похибка прогнозу
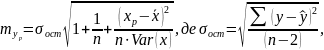
і будується довірчий інтервал прогнозу
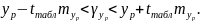
Інтервал може бути досить широкий за рахунок малого об'єму спостережень.
Регресії, нелінійні по включеним змінним, приводяться до лінійного виду простою заміною змінних, а подальша оцінка параметрів виконується за допомогою методу найменших квадратів.
Гіперболічна
регресія:
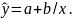
Лінеаризуюче
перетворення:
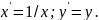
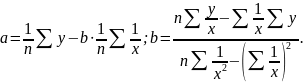
Регресії,
нелінійні за оцінюваними параметрами,
діляться на два типи:
внутрішньо нелінійні
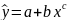 ,
,
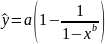 .і
т. п. (до лінійного виду не приводяться)
і внутрішньо лінійні
(приводяться до лінійного виду за
допомогою відповідних перетворень),
наприклад:
.і
т. п. (до лінійного виду не приводяться)
і внутрішньо лінійні
(приводяться до лінійного виду за
допомогою відповідних перетворень),
наприклад:
Експоненціальна
регресія:
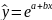 .
.
Лінеаризуюче
перетворення:
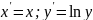 .
.
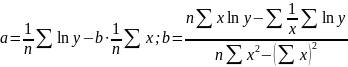
Степенева
регресія:
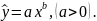
Лінеаризуюче
перетворення:
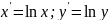 :
:
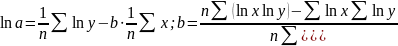
Показова
регресія:
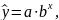
Лінеаризуюче
перетворення:
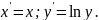
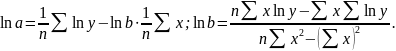
Логарифмічна
регресія:
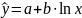 .
.
Лінеаризуюче
перетворення: