1.2.4 Способы определения положения точек на местности.
Положение любой точки местности определяют относительно каких-либо точек или линий, положение которых известно заранее, чаще всего относительно отрезков прямых, концы которых отмечены на местности специальными знаками.
Пусть требуется определить положение некоторой точки М местности относительно известных точек А и В, составляющих исходную прямую АВ. Возможны следующие простые и распространенные на практике способы решения такой задачи.
Способ перпендикуляров (способ прямоугольных координат). Опустим из точки М (рис. 1.2.4 ) на прямую АВ перпендикуляр, основание которого определится точкой С. Если измерить на местности величину перпендикуляра у = МО и расстояние х = АС от точки А до основания перпендикуляра С, то эти две линейные величины однозначно определят положение искомой точки М относительно исходного отрезка АВ. Длины х и у можно представить плоскими прямоугольными координатами точки М, поэтому описанный способ называют способом перпендикуляров или способом координат.
Рис. 1.2.4
Способ полярных координат. Положение искомой точки М можно определить, измерив в точке А горизонтальный угол α и горизонтальное расстояние АМ = 1. При этом прямую АВ называют полярной осью, а угол – полярным углом, отрезок l – радиусом вектором.
М
Рис. 1.2.5
Способ прямой угловой засечки. Положение точки М можно определить, измерив два горизонтальных угла α и β в точках А и В. При этом отрезок АВ = b называют базисом засечки. В этом способе положение точки М определяется, таким образом, двумя угловыми величинами α и β.
Рис. 1.2.6
Способ линейной засечки. Для определения положение точки М измеряют две линейные величины АМ = S1 и ВМ = S2. Базисом засечки b является отрезок АВ.
Рис. 1.2.7
1.2.5 Искажение расстояний
Небольшой участок сферической поверхности при определенных условиях можно принять за плоскость.
Применение модели плоской поверхности при решении геодезических задач возможно лишь для небольших участков поверхности Земли, когда искажения, вызванные заменой поверхности сферы или эллипсоида плоскостью невелики и могут быть вычислены по простым формулам. Это тем более оправдано, если учесть, что измерения на местности и чертежные работы всегда выполняются с ошибками, а потому небольшую часть сферы (эллипсоида), отличающуюся от плоскости на величину, меньшую ошибок измерений, можно считать плоской.
Рассчитаем, какое искажение получит дуга окружности, если заменить ее отрезком касательной к этой дуге. На рис.1.2.8 точка O - центр окружности, дуга ABC радиусом R стягивает центральный угол ε. Проведем касательную через середину дуги в точке B и, продолжив радиусы OA и OC до пересечения с касательной, получим точки A' и C'.
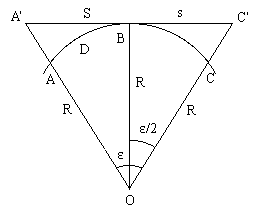
Рис.1.2.8
Пусть дуга ABC имеет длину D, а отрезок касательной A'C' - длину S. Известно, что для окружности D = R* ε, причем угол ε должен быть выражен в радианах.
Из ΔOBC' имеем:
S/2=R*tg(ε/2) или S = 2 R tg(ε/2) (1.2.1)
Разность (S - D) обозначим через ΔD и напишем
ΔD=R*[2*tg( ε/2)- ε] (1.2.2)
Разложим tg(ε/2) в ряд, ограничившись ввиду малости угла ε/2 двумя членами разложения,
или
.
Подставим это выражение в формулу (1.2.2) и получим
.
Но ε = D/R, поэтому
.
Отношение ΔD/D называется относительным искажением длины дуги при замене ее отрезком касательной, оно будет равно:
(1.2.3)
Абсолютные и относительные значения погрешностей, вычисленные соответственно по формулам (1.2.2) и 1.2.3) для участков земной поверхности, приведены ниже. Для расчетов радиус Земли R взят равным 6370 км:
D, км |
10 |
20 |
25 |
50 |
100 |
ΔD, см |
1 |
7 |
13 |
103 |
821 |
ΔD/D |
1:1 000 000 |
1:300 000 |
1:200 000 |
1:49 000 |
1:12 000 |
Учитывая реальную точность с которой теперь производят измерения линий на местности при геодезических работах участок сферы 20 х 20 км можно считать плоским, погрешности от замены уровенной поверхности плоскостью не имеют практического значения.. При работах пониженной точности размеры участка сферы, принимаемого за плоскость, можно увеличить.