Міністерство освіти і науки України

Східноєвропейський національний університет імені Лесі Українки

Математичний факультет

Дипломна робота Розв’язність геометричних задач на побудову за допомогою циркуля і лінійки

Підготувала:

студентка 51 групи

Занюк Лілія

Науковий керівник:

доц. Волошина Т. В.

Луцьк – 2014

План

Вступ. Історичні відомості

Розділ І. Скінченні розширення полів.

1.1 Скінченні розширення полів.

1.2 Алгебраїчні розширення полів.

1.3 Алгебраїчні та трансцендентні числа.

1.4 Поле розкладу многочлена.

Розділ ІІ. Основи теорії Галуа.

2.1 Розширення Галуа та група Галуа. Група Галуа многочлена.

2.2 Радикальні та квадратично-радикальні розширення полів.

Розв’язність рівнянь в квадратичних радикалах.

Розділ ІІІ. Розв’язність задач на побудову за допомогою циркуля та лінійки.

3.1 Нерозв’язність задачі трисекції кута, подвоєння куба.

3.2 Теореми Гауса, застосування її до розв’язності задачі на побудову правильного многокутника.

Висновки

Література

Розділ і. Скінченні розширення полів.

1.1 Скінченні розширення полів

Кільце R — це множина з двома бінарними операціями, що звичайно позначаються "+" та "*" і називаються додаванням та множенням, яка задовільняє наступній системі аксіом:

• (R,+)  є комутативною групою. Її називають адитивною групою кільця і нейтральний елемент в ній позначають як 0 (нуль);

•   (дистрибутивність  додавання щодо множення);

•  (асоціативність множення);

• в (R, ) існує нейтральний елемент 1 (одиниця), що задовільняє:  .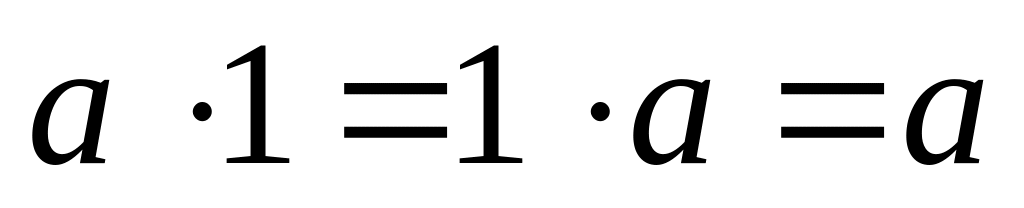

кільця, в яких множення асоціативне, називають асоціативними кільцями.

Кільця що задовольняють вимогу  комутативності  множення  ab=ba.  називають комутативними кільцями. Не всі кільця є комутативними, наприклад, кільце матриць.

Полем називається асоціативно-комутативне кільце, в якому є хоча б один, відмінний від нуля елемент і в якому рівняння a x = b має розв'язки при будь-якому а   0 і будь-якому b .

Означення. Числовим полем називається всяке числове кільце, замкнуте щодо ділення (виключаючи ділення на 0).

Якщо підмножина Р поля F сама утворює поле щодо операцій в F (з тими самими нулем і одиницею), то P називається підполем  F,  а  F — розширенням поля P. Позначається F=P(θ).

Розширення поля F=P(θ) називається простим якщо існує елемент θ в полі P, такий що єдиним підполем поля F, що містить як P так і θ є саме поле F.

Для довільного поля F, многочлен f(x)  з коефіцієнтами в  F  (такі многочлени утворюють кільце F[x]) називається незвідним у полі   якщо він не рівний константі і не дорівнює добутку двох або більше многочленів з F[x] , що не є константами. Дана властивість залежить від поля F; многочлен, що є незвідним в одному полі може розкладатися на добуток в іншому.

Поле розкладу многочлена p над полем K — найменше розширення поля, над яким p розкладається в добуток лінійних множників:

.

При цьому   , тому поле розкладу L також називається розширенням, одержаним приєднанням до  K  всіх  коренів даного многочлена.

Нехай корінь многочлена степеня над полем :

. (1)

Вважатимемо, що многочлен (1) незвідний в полі , бо в протилежному випадку ми могли б розглядати той незвідний множник многочлена, який має своїм коренем.

Якщо – будь-який інший многочлен над полем , коренем якого є , то, внаслідок незвідності , многочлен ділиться на (взаємно простими вони бути не можуть, бо мають спільний множник ) і тому має степінь не нижчий за . Зокрема, якщо – також незвідний многочлен, то він збігається з з точністю до сталого множника. Отже, зведений многочлен – єдиний незвідний многочлен над полем , який має своїм коренем, а його степінь – найнижчий серед степенів усіх многочленів з коренем .

Тому доцільно назвати ‒ мінімальним многочленом числа , а його степінь ‒ степенем алгебраїчного числа відносно поля .

З’ясуємо властивості розширення поля ( ) у випадку, коли є алгебраїчним числом -го степеня відносно поля . Будова такого розширення характеризується такою теоремою.

Теорема 1. Поле Р( ), утворене з поля Р приєднанням кореня незвідного у полі Р многочлена п-го степеня

,

складається з усіх чисел виду =c₀+c₁ +c₂ ²+...+c_n-1 ^{n- 1} , (2)

де c₀, c₁,...,c_n-1 – довільні числа з поля Р.

Доведення: Спочатку доведемо, що всі числа виду (2) утворюють поле. Той факт, що сума і різниця чисел виду (2) є числом такого ж виду – очевидний. Розглянемо добуток і частку цих чисел. Ясно, що число виду (2) можна розглядати як результат підстановки замість х у деякий многочлен q(x) над полем Р не вище (п-1) степеня : .

Нехай маємо два числа , . Тоді добуток , де – многочлен, степінь якого вже може

перевищувати п-1. Поділимо на f(x) з остачею. Маємо:

=f(x)∙ +r(x), (3)

де степінь остачі r(x) менший за степінь f(x), тобто не перевищує п-1. Підставивши у вираз (3), одержимо (бо f( )=0), тобто . Іншими словами, добуток чисел і є числом виду (2), бо r(x) – многочлен, степінь якого не перевищує п-1.

Розглянемо частку. Тут досить показати, що для будь-якого числа ≠ 0 виду (2) число теж буде числом виду (2) (бо при множенні q( ) на якесь t( ) буде многочлен того ж виду). Оскільки f(x) – незвідний у полі Р многочлен, то многочлен q(x) або взаємно простий з f(x), або ділиться на f(x). Але другий випадок неможливий, бо q(x) має степінь, менший ніж степінь мінімального многочлена f(x). Тому (f, g)=1.

Отже, існує єдина пара многочленів і таких, що справджується тотожність

f(x)∙ +q(x)∙ =1.

Підставивши х= і врахувавши, що f( )=0, одержимо q( )∙ =1, тобто . Отже, . Якщо многочлен має степінь, менший за п, то твердження доведено. Якщо ж має степінь, не менший за п, то ділимо на многочлен f(x), тобто =f(x)∙ +r(x), звідси =r( )= , і степінь r(x) менший за степінь f(x). Отже, є числом виду (2).

Отже, числа виду (2) утворюють поле Р₁. Доведемо, що Р₁=Р( ). Оскільки поле Р₁ містить як поле Р, так і число , то воно містить і Р( ), яке за означенням є мінімальним полем з такими властивостями, тобто Р₁ Р( ).

З другого боку, будь-яке поле, яке включає і поле Р, повинно включати і всі числа виду (2), які утворюються з чисел поля Р і числа за допомогою дій множення і додавання. Отже, Р( ) Р₁. Звідси Р₁=Р( ). Теорема доведена.

Наслідок. Якщо – корінь многочлена другого степеня над полем Р f(x)=x²+px+q,

причому Р, то просте розширення Р( ) поля Р, утворене приєднанням числа , складається з усіх чисел виду , де a, b – довільні числа з поля Р.

Наведемо кілька прикладів.

1. Поле R( ) утворене приєднанням до поля R кореня незвідного в полі R многочлена другого степеня f(x)=x²-2. Елементи поля R( ) мають вигляд a+b , де a, b – раціональні числа.

2. Розглянемо будову елементів . Число = є коренем незвідного в полі R многочлена третього степеня . Тому всі елементи поля за теоремою 1 мають вигляд =c₀+c₁ +c₂ , де с₀, с₁, с₂ ‒ раціональні числа.

3. Поле К комплексних чисел утворюється з поля D дійсних чисел приєднанням до нього кореня і незвідного в D многочлена 2-го степеня . З доведеної теореми випливає, що всі елементи , тобто всі комплексні числа, мають вигляд , де ‒ дійсні числа.

Теорема 1 і наведений приклад свідчать про те, що числа поля Р( ) мають специфічну структуру: вони являють собою суму виду

=с₀+с₁ +с₂ ²+...+с_п-1 ^п-1,

де кожний член є добутком елемента c_k поля Р на елемент ^k (k=0,1,2,...,n-1) поля Р( ). Тобто можна сказати, що довільний елемент поля Р( ), де - корінь незвідного в полі Р многочлена степеня n, є лінійною комбінацією елементів , , ²,..., ^n-1 з коефіцієнтами з поля Р. Тому для вивчення властивостей розширення слід спинитися більш детально на понятті лінійної комбінації і на зв’язаних з ним поняттях лінійної залежності і лінійної незалежності елементів відносно деякого поля .

Нехай елементи належать полю . Елементи ж братимемо лише з його підполя . Сукупність чисел називатимемо лінійно незалежною системою елементів відносно поля , якщо рівність

(4)

можлива лише при всіх . Якщо ж рівність (4) справджується і тоді, коли хоч одне з не дорівнює нулю, то система елементів називається лінійно залежною відносно поля .

Проілюструємо ці означення прикладами.

1. В полі R( ) числа α₁=1, α₂= є лінійно незалежною системою елементів відносно поля R. Дійсно, нехай . Складемо рівність (4) для цього випадку: . Покажемо, що тут . Припустимо супротивне, тобто, що (випадок, коли одне з дорівнює, а друге не дорівнює нулю, неможливий, що видно безпосередньо). Тоді маємо , тобто є раціональне число, що неможливо. Отже, припущення не вірне, α_1, α₂ тут є лінійно незалежними.

2. В тому самому полі R( ) два числа і можуть бути лінійно залежною системою елементів відносно поля R. Дійсно, з рівності при умові, наприклад, маємо , або

= ( ).

Отже, числа α_1, і α₂ тут є лінійно залежними відносно поля R, якщо вони задовольняють умови , , тобто коли справджується рівність .

Зазначимо тепер деякі прості властивості лінійно залежних і лінійно незалежних систем елементів.

1. Кожна частина лінійно незалежної системи елементів відносно поля є також лінійно незалежною системою елементів відносно поля .

2. Будь-яка система елементів поля , яка включає число нуль (нуль належить кожному полю), є лінійно залежною відносно поля Р.

Повернемося тепер до результатів теореми 1. Ця теорема з’ясовує структуру розширення ( ) поля Р, де – корінь незвідного в полі Р многочлена f(x) n-го степеня. Поле ( ) побудоване так: існує n елементів цього поля таких, що кожний елемент є лінійною комбінацією цих елементів з коефіцієнтами з поля P.

Покажемо, що сукупність чисел 1, , ²,..., ^n-1 є лінійно незалежною системою елементів відносно поля Р. Дійсно, запишемо рівність: λ₀1+λ₁ +...+λ_n-1 ^n-1=0, де λ_i P. Якщо ця рівність справджується, коли не всі λ_i дорівнюють 0 (тобто 1, , ²,..., ^n-1 – лінійно залежні), то це означає що є коренем деякого многочлена =λ₀+λ₁x+...+λ_n-1x^n-1 з коефіцієнтами з поля Р, степінь якого не перевищує п-1. Але це неможливо, бо многочлен f(x) степеня п є мінімальним многочленом числа .

Отже, якщо - алгебраїчне число п-го степеня відносно поля Р, то елементи розширення P( ) є лінійними комбінаціями (з коефіцієнтами з поля Р) елементів лінійно незалежної відносно Р системи 1, , ²,..., ^n-1.

Означення. Розширення поля Р називається скінченним, якщо в

полі існує така лінійно незалежна відносно поля Р система елементів ₁, ₂,..., _n, що будь-який елемент є лінійною комбінацією цих елементів з коефіцієнтами з поля Р:

=λ_{1 1}+λ_{2 2}+...+λ_{n n}. (5)

Система елементів ₁, ₂,..., _n називається базисом поля відносно поля Р.

Базис скінченого розширення можна вибрати не одним способом. Проте всі базиси поля мають те саме число елементів п. Більш того: довільна лінійно незалежна система з n елементів є базисом. Число п є характеристикою скінченного розширення поля Р, незалежно від вибору базису. Число п називається степенем розширення над полем Р і позначається ( :Р).

Степінь п скінченого розширення над полем Р дорівнює максимальному числу l елементів поля , які можуть утворювати лінійно незалежну систему. Справедливе і обернене твердження, а саме:

Якщо l – максимальне число елементів розширення поля Р, що утворюють лінійно незалежну систему відносно поля Р, то є скінченим розширенням над полем Р степеня l.

Наведемо кілька прикладів скінченних розширень полів.

1. Поле R( ) чисел виду a+b , де a, b – довільні раціональні числа, є розширенням поля R степеня 2, бо існує базис поля R( ) відносно поля R, який складається з двох елементів. За базис можна взяти числа 1 і , або 1+ і 1- , або взагалі два числа a₁+b₁ i a₂+b₂ , щоб тільки система цих чисел була лінійно незалежною відносно R, тобто щоб справджувалась умова .

2. Поле є скінченним розширенням степеня 3 поля R. Базисом цього поля відносно поля R є, наприклад, числа 1, , або 1+ , 2‒ , 1+ .

3. Поле К комплексних чисел відносно поля D дійсних чисел є скінченним розширенням степеня 2. Базисом поля К відносно поля D, є, наприклад, система чисел 1 і і.

Не кожне розширення поля є скінченим. Наприклад поле D дійсних чисел є розширенням поля R раціональних чисел, однак це розширення не є скінченим, бо в ньому не існує скінченого базису, через який лінійно виражалося б будь-яке дійсне число.

Розширення першого степеня над полем Р просто збігається з полем Р. Справді, довільний елемент в цьому випадку має вигляд , де – деякий фіксований елемент поля , а λ – будь-яке число з поля Р. якщо взяти, наприклад, , то знайдеться таке, що , звідки . Як бачимо, , а разом з ним і кожне належать полю P, тобто . Оскільки ж ‒ розширення Р, то дістаємо = Р.