Вопрос 2. Фигуры и модусы категорического силлогизма.
В посылках простого категорического силлогизма средний термин может в каждом из двух суждений занимать место или субъекта или предиката. Нетрудно увидеть, что существует четыре варианта расположения среднего термина в посылках. Эти варианты расположения среднего термина в посылках получили название – ФИГУРЫ СИЛЛОГИЗМА. Номера фигур закреплены за каждым вариантом расположения среднего термина.
В ПЕРВОЙ ФИГУРЕ средний термин занимает место субъекта в большей посылке и место предиката в меньшей посылке. Схематически это выглядит так:
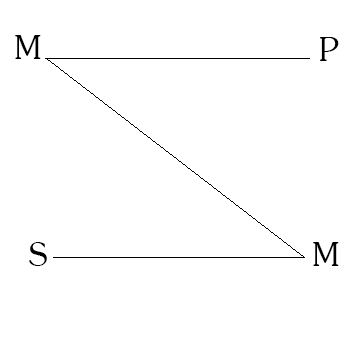
Пример:
Все щелочноземельные металлы (М) двухвалентны (Р).
Стронций (S) – щелочноземельный металл (М).
______________________________________________
Стронций (S) – двухвалентен (Р).
Во ВТОРОЙ ФИГУРЕ средний термин занимает место предиката в обеих посылках. На схеме:
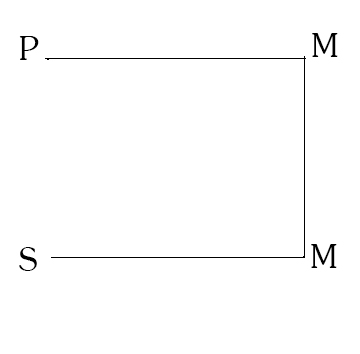
Пример:
Все юристы (Р) имеют юридическое образование (М).
Некоторые из присутствующих(S) не имеют юридического образования (М).
Некоторые из присутствующих (S) не являются юристами (Р).
В ТРЕТЬЕЙ ФИГУРЕ средний термин занимает место субъекта в обеих посылках. На схеме:
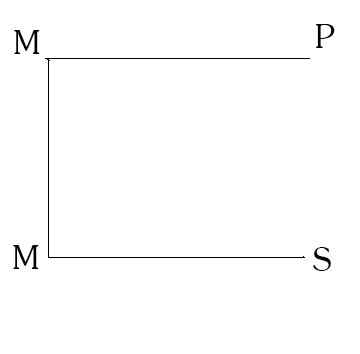Пример:
Все бамбуки (М) цветут один раз в жизни (Р).
Все бамбуки (М) – многолетние растения (S).
_______________________________________
Некоторые многолетние растения цветут один раз в жизни.
В ЧЕТВЕРТОЙ ФИГУРЕ средний термин занимает место предиката в большей посылке и место субъекта – в меньшей. На схеме:
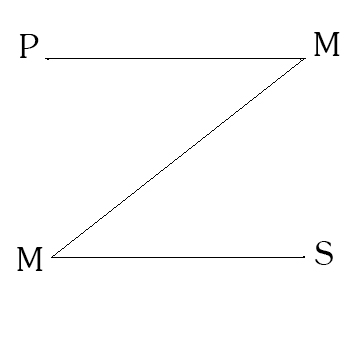Пример:
Ни один богатый человек (Р) не стремится к справедливости (М).
Некоторые стремящиеся к справедливости люди (М) являются
юристами (S).
__________________________________________________
Некоторые юристы (S) не являются богатыми людьми (Р).
Кроме общих правил силлогизма, каждая из фигур имеет и свои особые правила:
Правила фигур силлогизма
Правила 1й фигуры:
Большая посылка – общее суждение
Меньшая посылка – утвердительное суждение
Правила 2й фигуры:
Большая посылка – общее суждение
Меньшая посылка – отрицательное суждение
Правила 3й фигуры:
Меньшая посылка – утвердительное суждение
Заключение – частное суждение
Правила 4й фигуры :
1.Если большая посылка утвердительная, то меньшая должна быть общей.
2.Если одна из посылок отрицательная, то большая должна быть общей.
Кроме фигур, силлогизмы различаются еще и модусами.
МОДУСЫ простого категорического силлогизма – это разновидности силлогизма, различающиеся типами суждений входящих в состав силлогизма. Обозначается силлогизм буквами, характеризующими типы суждений входящих в него. Так как в простом категорическом силлогизме три суждения (две посылки и одно заключение), то каждый силлогизм в своем полном обозначении имеет три буквы.
Каждая фигура силлогизма имеет 64 модуса. Таким образом, возможны 256 различных способов вывода по схемам категорического силлогизма. Однако, еще со времен Аристотеля известно, что правильных модусов лишь 19 (24). В классической логике все правильные модусы имеют собственные имена на латыни. В этих именах гласные буквы соответствуют типам суждений, входящих в данный модус. Вот имена этих правильных модусов:
В первой фигуре: Barbara (AAA), Darii (AII), Celarent (EAE), Ferio (EIO).
Вовторой: Cesare (EAE), Camestres (AEE), Festino (EIO), Baroco (AOO).
Втретьей: Darapti (AAI), Disamis (IAI), Datisi (AII), Felapton (EAO), Bocardo (OAO), Ferison (EIO).
Вчетвертой: Bramantip (AAI), Camenes (AEE), Dimaris (IAI), Fesapo (EAO), Fresison (EIO).
В тех случаях, когда в заключения силлогизма попадают общие суждения, допустима и замена их на частные. Таким образом, к 19-ти перечисленным модусам можно добавить еще 5: ААА – ААI, ЕАЕ – ЕАО в первой фигуре; ЕАЕ – ЕАО, АЕЕ – АЕО во второй; АЕЕ – АЕО в четвертой.
Определить правильность или неправильность какого-либо рассуждения, проведенного по схемам категорического силлогизма достаточно просто: надо определить фигуру и модус вашего рассуждения и посмотреть попадает или нет эта фигура в число правильных. Если попадает, то рассуждение проведено верно, если не попадает, то умозаключение неправильно.