Тема 7. Непосредственные умозаключения.
Вопросы:
Выводы по логическому квадрату.
Выводы с преобразованием внутренней структуры суждений:
А) Обверсия; Б) Конверсия; В) Контрапозиция; Г) Инверсия.
Вопрос 1. Выводы по логическому квадрату.
В практике часто бывают случаи, когда нам известна истинность или ложность одного из типов категорических суждений А, Е, I, О. А нам требуется знать истинность и ложность всех остальных суждений, имеющих тот же субъект и предикат. Например, нам известно, что суждение «Некоторые парты в этой аудитории сломаны» является истинным суждением» (I). Исходя из этого, требуется определить истинность и ложность суждений: «Все парты в этой аудитории сломанные» (А); «Ни одна парта в этой аудитории не является сломанной» (Е); «Некоторые парты в этой аудитории не являются сломанными» (О). Если бы я сейчас задал вам эту задачу, то она отняла бы у вас достаточно много времени и все равно многие ее решили бы неправильно. Между тем в логике есть и теория, и процедура знание которых позволяет почти молниеносно решать подобные задачи формальным образом, не прибегая к содержательным рассуждениям. Эта теория и эта процедура известны как отношения суждений в логическом квадрате или выводы по логическому квадрату.
ЛОГИЧЕСКИЙ
КВАДРАТ – это геометрический квадрат,
в котором расставлены суждения, имеющие
одно и тоже содержание (один и тот же
субъект и предикат), но разную логическую
форму (т. е. относящиеся к различным
типам А, Е, I, О) следующим образом: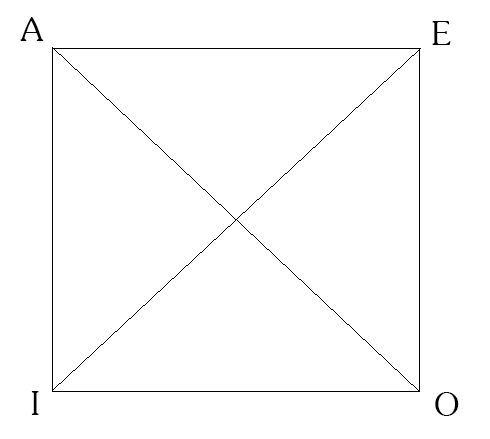
По теории между суждениями в этом логическом квадрате существуют следующие отношения:
Суждения А и Е называются противоположными или КОНТРАРНЫМИ. Эти суждения подчиняются правилу: КОНТРАРНЫЕ суждения никогда не могут быть вместе истинными. Отсюда следует:
А(и) Е(л)
Е(и) А(л)
В тех же случаях, когда первое суждение оказывается ложным, второе может быть как истинным, так и ложным (т. е. остается неопределенным):
А(л) Е(неопр.)
Е(л) А(неопр.)
Суждения I и О называются СУБКОНТРАРНЫМИ суждениями.
Эти суждения подчиняются правилу: СУБКОНТРАРНЫЕ суждения никогда не могут быть вместе ложными. Отсюда следует:
I(л) О(и)
О(л) I(и)
В тех случаях, когда первое суждение оказывается истинным, второе суждение будет неопределенным:
I(и) О(неопр.)
О(и) I(неопр.)
Отношения между суждениями А и I, и суждениями Е и О называются отношениями ПОДЧИНЕНИЯ. Общие суждения здесь будут называться ПОДЧИНЯЮЩИМИ, а частные – ПОДЧИНЕННЫМИ. Для этих суждений действует следующее правило: Если ПОДЧИНЯЮЩЕЕ суждение истинно, то ПОДЧИНЕННОЕ ему суждение тоже будет истинным; если ПОДЧИНЕННОЕ суждение ложно, то ПОДЧИНЯЮЩЕЕ его суждение тоже будет ложным. Если мы посмотрим на логический квадрат, то отметим, что может «опускаться», а ложь «подниматься». Символически это можно записать следующим способом:
А(и) I(и)
Е(и) О(и)
I(л) А(л)
О(л) Е(л)
В тех случаях, когда ПОДЧИНЯЮЩЕЕ суждение будет ложным или ПОДЧИНЕННОЕ будет истинным, суждение, связанное с ним вертикалью квадрата будет неопределенным:
А(л) I(неопр.)
Е(л) О(неопр.)
I(и) А(неопр.)
О(и) Е(неопр.)
Суждения, расположенные по диагоналям логического квадрата: А О и Е I называются (в паре) противоречащими или КОНТРАДИКТОРНЫМИ суждениями. Отношения между ними подчиняются следующему правилу: КОНТРАДИКТОРНЫЕ суждения никогда вместе не могут быть истинными и никогда вместе не могут быть ложными. Таким образом, расположенные по диагонали квадрата суждения всегда имеют противоположные значения истины и лжи:
А(и) О(л)
А(л) О(и)
Е(и) I(л)
Е(л) I(и)
I(и) Е(л)
I(л) Е(и)
О(и) А(л)
О(л) А(и)
Исходя из этого, можно быстро решить нашу задачу с партами. Нам известно, что суждение «Некоторые парты в этой аудитории сломанные» является истинным. Так как это суждение I, то КОНТРАДИКТОРНОЕ (расположенное по диагонали) суждение Е «Ни одна парта в этой аудитории не является сломанной» будет ложным.
По отношению к суждению А «Все парты в этой аудитории являются сломанными» это суждение будет подчиненным. Истинность подчиненного суждения оставляет неопределенным истинность подчиняющего и таким образом суждение А будет неопределенным. С суждением О «Некоторые парты в этой аудитории не являются сломанными» наше исходное суждение будет находиться в отношениях СУБКОНТРАРНОСТИ, а это означает, что истинность первого не позволяет нам определить истинность или ложность второго, так что суждение О также как и А останется неопределенным.