16.Матрицалық алгебраны қолданумен, халықаралық қор алаңдарында портфелдiң табыстылығын есептеу

Наиболее просто производится подсчет, если за рассматриваемый период внесенные средства оставались без изменений. Тогда можно воспользоваться формулой, которую мы уже успели вспомнить:

((Р1 – Р0) / Р0) х 100%.

Таким образом, если в начале года на вашем счете было 100 тыс. руб., а к его концу сумма увеличилась до 125 тыс., то годовая доходность составит ((125 000 – 100 000) / 100 000) х 100% = 25%.

Универсальная формула

Таким образом, если у нас имеется N подпериодов с доходами r1, r2… rN соответственно, то итоговая формула для расчета прибыльности портфеля за весь период будет выглядеть так:

(1 + r1) х (1 + r2) х … х (1 + rN) – 1.

Однако поскольку нам всегда известно состояние портфеля в начале и конце подпериода, то данную формулу можно переписать иначе:

(P1к / P1н) х (P2к / P2н) х … х (Pnк / Pnн) – 1,

где P1н — стоимость портфеля в начале первого подпериода;

P 1 к  — в его конце;

P 2 н  — стоимость в начале второго подпериода;

P 2 к  — в его конце и т. д., вплоть до энного подпериода.

17.Матрицалық алгебраны қолданумен, халықаралық қор алаңдарында портфелдiң тәуекелдiгін есептеу

Eсли объединять портфели ценных бумаг с корреляцией +1, то риск портфеля не уменьшается, а только усредняется. Идеальным портфелем можно считать только такой портфель, где корреляция равна -1. Риск портфеля ценных бумаг становиться меньше средневзвешенной суммы рисков, когда между активами корреляция отрицательная. Поэтому, если инвестор формирует актив с низкой корреляцией доходностей, то данный случай называют хеджированием.

Для оценки риска портфеля ценных бумаг необходимо в первую очередь рассчитать среднюю фактическую доходность данного портфеля за n-периодов, следующим этапом является расчет риска портфеля по показателю среднеквадратического отклонения, а уже последним этапом (третьим) является сравнение совокупный коэффициент вариации с другими портфелями ценных бумаг, который рассчитывается по формуле 5 (рисунок 5), где iр – средняя фактическая доходность портфеля ценных бумаг за n периодов, а сигма р – среднеквадратическое отклонение портфеля ценных бумаг.

 

ОООО

Оперативтік және қаржылық леверидж

Понятие «леверидж» происходит от английского «leverage - действие рычага», и означает соотношение одной величины к другой, при небольшом изменении которого сильно меняются связанные с ним показатели.

    Наиболее распространены следующие виды левериджа:

Производственный (операционный) леверидж.

Финансовый леверидж.

    Все компании в той или иной степени используют финансовый леверидж. Весь вопрос в том, каково разумное соотношение между собственным и заемным капиталом.

    Коэффициент финансового левериджа (плечо финансового рычага) определяется как отношение заемного капитала к собственному капиталу. Правильнее всего рассчитывать его по рыночной оценке активов.

Рассчитывается также эффект финансового рычага:

ЭФР = (1 - Кн)*(ROA - Цзк) * ЗК/СК.

где ROA - рентабельность совокупного капитала до уплаты налогов (отношение валовой прибыли к средней стоимости активов), %;

СК - среднегодовая сумма собственного капитала;

Кн - коэффициент налогообложения, в виде десятичной дроби;

Цзк - средневзвешенная цена заемного капитала, %;

ЗК - среднегодовая сумма заемного капитала.

Формула расчета эффекта финансового рычага содержит три сомножителя:

(1 - Кн) — не зависит от предприятия.

(ROA - Цзк) — разница между рентабельностью активов и процентной ставкой за кредит. Носит название дифференциал (Д).

(ЗК/СК) — финансовый рычаг (ФР).

Можно записать формулу эффекта финансового рычага короче:

ЭФР = (1 - Кн) ? Д ? ФР.

    Эффект финансового рычага показывает, на сколько процентов увеличивается рентабельность собственного капитала за счет привлечения заемных средств. Эффект финансового рычага возникает за счет разницы между рентабельностью активов и стоимостью заемных средств. Рекомендуемое значение ЭФР равняется 0.33 - 0.5.

    Получаемый эффект от финансового левериджа заключается в том, что использование долговой нагрузки при прочих равных условиях приводит к тому, что рост прибыли корпорации до уплаты процентных платежей и налогов ведет к более сильному росту показателя прибыли на акцию.

    Также рассчитывают эффект финансового рычага с учетом действия инфляции (долги и проценты по ним не индексируются). При увеличении уровня инфляции плата за пользование заемными средствами становится ниже (процентные ставки фиксированные) и результат от их использования выше. Однако, если процентные ставки высоки или невысока доходность активов - финансовый леверидж начинает работать против собственников.

    Леверидж - весьма рискованное дело для тех предприятий, деятельность которых носит циклический характер. В результате несколько последовательных лет с низкими продажами могут привести предприятия, обремененные высоким левериджем, к банкротству.

    Для более подробного анализа изменения значения коэффициента финансового левериджа и факторов повлиявших на это используют методику 5-и факторный анализ коэффициента финансового левериджа.

Таким образом, финансовый леверидж отражает степень зависимости предприятия от кредиторов, то есть величину риска потери платежеспособности. Кроме этого предприятие получает возможность воспользоваться «налоговым щитом», так как в отличие от дивидендов по акциям сумма процентов за кредит вычитается из общей величины прибыли, подлежащей налогообложению.

Операционный рычаг (операционный леверидж) показывает во сколько раз темпы изменения прибыли от продаж превышают темпы изменения выручки от продаж. Зная операционный рычаг можно прогнозировать изменение прибыли при изменении выручки.

Это соотношение постоянных и переменных расходов компании и влияние этого отношения на прибыль до вычета процентов и налогов (операционную прибыль). Операционный рычаг показывает, на сколько процентов изменится прибыль при изменении выручки на 1%.

Ценовой операционный рычаг вычисляется по формуле:

Рц = В/П

Учитывая, что В = П + Зпер + Зпост, можно записать:

Рц = (П + Зпер + Зпост)/П =1 + Зпер/П + Зпост/П

где: В — выручка от продаж.

П — прибыль от продаж.

Зпер — переменные затраты.

Зпост — постоянные затраты.

Рц — ценовой операционный рычаг.

Рн — натуральный операционный рычаг.

Натуральный операционный рычаг вычисляется по формуле:

Рн = (В-Зпер)/П

Учитывая, что В = П + Зпер + Зпост, можно записать:

Рн = (П + Зпост)/П = 1 + Зпост/П

Операционный леверидж используется менеджерами для того, чтобы сбалансировать различные виды затрат и увеличить соответственно доход. Операционный леверидж дает возможность увеличить прибыль при изменении соотношения переменных и постоянных затрат.

Положение о том, что постоянные издержки при изменении объема производства остаются неизменными, а переменные — линейно возрастают, позволяет значительно упростить анализ операционного рычага. Но известно, что реальные зависимости сложнее.

С ростом объема производства переменные издержки на единицу продукции могут как уменьшаться (использование прогрессивных технологических процессов, совершенствование организации производства и труда), так и увеличиваться (рост потерь в брак, снижение производительности труда и т.д.). Темпы роста выручки замедляются из-за снижения цен на товар по мере насыщения рынка.

Финансовый леверидж и операционный леверидж – близкие методы. Как и в случае операционного левериджа, финансовый леверидж повышает постоянные издержки в форме выплат высокого процента за кредит, но поскольку кредиторы не участвуют в распределении доходов компании, снижаются переменные издержки. Соответственно, возросший финансовый леверидж также оказывает двоякое воздействие: требуется больше операционного дохода для покрытия постоянных финансовых издержек, но когда достигается окупаемость затрат, прибыль начинает расти быстрей с ростом каждой единицы дополнительного операционного дохода.

Совместное влияние операционного и финансового рычагов известно как эффект общего рычага и представляет собой их произведение:

Общий рычаг = ОЛ х ФЛ

Этот показатель дает представление о том, как изменение продаж повлияет на изменение чистой прибыли и дохода на акцию предприятия. Другими словами, он позволит определить, на сколько процентов изменится чистая прибыль при изменении объема продаж на 1%.

Поэтому производственный и финансовый риски мультиплицируются и формируют совокупный риск предприятия.

Таким образом, как и финансовый, так и операционный леверидж, оба потенциально эффективные, могут оказаться очень опасными из-за рисков, которые они содержат в себе. Хитрость, а точнее умелое управление финансами, состоит в том, чтобы уравновесить эти два элемента.

Нақты опциондарды жүйеге келтіру.

Для того чтобы выявить различные типы операционной и стратегической гибкости, мы можем разбить опционы, связанные с активами, на пять взаи­моисключающих (но не исчерпывающих) категорий.

Опцион на прекращение проекта/выход из бизнеса. Опцион на прекра­щение (или продажу) проекта — скажем, возможность покинуть действую­щую угольную шахту - формально эквивалентен американскому опциону «пут* на акции. При неблагоприятном обороте событий к концу первого периода принимающий решение может отказаться от проекта и реализо­вать его ожидаемую ликвидационную стоимость, которую можно рассмат­ривать как цену исполнения опциона «путь. Когда приведенная стоимость активов падает ниже их ликвидационной стоимости (цены продажи), акт прекращения (продажи) проекта равнозначен исполнению опциона «пут». Поскольку ликвидационная стоимость образует нижний предел стоимости проекта, опцион на прекращение обладает ценностью. Следовательно, проект, который можно прекратить, стоит дороже такого же проекта, но не дающего этой возможности.

Опцион на отсрочку развития. Опцион на отсрочку инвестиций в разви­тие материальной базы формально эквивалентен американскому опциону «колл» на акции. К примеру, владелец лицензии на разработку неосвоенно­го нефтяного месторождения вправе приобрести уже освоенное месторож­дение, оплатив все лицензионные и арендные издержки освоения. Однако владелец лицензии может отложить развитие до тех пор, пока не поднимут­ся цены на нефть Иными словами, управленческий опцион, сопряженный с владением неосвоенным месторождением, представляет собой опцион на отсрочку. Ожидаемые затраты на освоение можно рассматривать как цену исполнения опциона «колл» Чистый доход от производства за вычетом истощения запасов в результате разработки месторождения — это альтер­нативные издержки отсрочки инвестиций. Если альтернативные издержки слишком велики, то принимающий решение может предпочесть исполнить опцион (т. е. начать разработку месторождения), не дожидаясь истечения его срока.

Опцион на расширение или сокращение. Опцион на расширение масшта­бов проекта формально эквивалентен американскому опциону «колл» на акции. Например, руководство компании может принять решение постро­ить производственное предприятие с избыточной для планируемого объема выпуска мощностью, чтобы впоследствии иметь возможность увеличить производство, если реализация продукта пойдет успешнее, чем ожидается. Опцион на расширение наделяет менеджеров правом (но не обязанностью!) при благоприятном для проекта стечении обстоятельств в дальнейшем осуществлять дополнительные инвестиции (скажем, для увеличения тем­пов производства). Опцион на сокращение масштабов проекта формально эквивалентен американскому опциону «пут» на акции. Многие проекты можно организовать таким образом, чтобы в дальнейшем без особых уси­лий свернуть объем производства. Предполагаемые на будущее расходы по проекту равнозначны цене исполнения опциона «пут».

Опцион на продление или досрочное завершение проекта. Нередко бывает возможно продлить срок полезной службы актива или действие контракта за определенную сумму денег - цену исполнения опциона. Возможно и обратное: досрочно вывести актив из эксплуатации или пре­рвать контракт. Опцион на продление представляет собой «колл», а опцион на досрочное завершение — «пут». Соглашения об аренде недвижимости зачастую содержат оговорки, за которыми, по сути, кроется опцион на про-дление или досрочное завершение лизинга.

Опцион на увеличение или уменьшение охвата. Охват проекта - это количество причастных к нему видов деятельности. Опционный характер этого свойства проекта выражается в способности на каком-то этапе в бу­дущем сменить направление деятельности. Охват подобен диверсификации иногда — при увеличении цены исполнения - совсем не вредно иметь воз­можность выбора из широкого набора вариантов. Опцион на увеличение охвата представляет собой «колл».

Опционы на переключение. Опцион на переключение (запуск/приостаиовку) проекта, в сущности, представляет собой портфель опционов, куда входят и «коллы», и «путы». Например, возможность возобновить операции по временно замороженному проекту эквивалентна американ­скому «коллу», а приостановить деятельность (закрыть предприятие) в неблагоприятных обстоятельствах — американскому «путу». Издержки возобновления (или остановки) операций можно рассматривать как цену исполнения «колла» (или «пута»). Проект, позволяющий быстро переклю­чаться с активной деятельности на полное ее сворачивание (или с одного предприятия на другое и т. п.), стоит дороже аналогичного проекта, ноне обладающего подобной гибкостью. Такого рода опционы заключены, на­пример, в гибкой производственной системе, способной выпускать несколь­ко видов продукции, или в электроэнергетическом предприятии, которое может работать на нескольких видах топлива, или в возможности покинуть отрасль, а потом вновь туда вернуться.

Сложные опционы. Это опционы на опционы. Ярким примером могут слу­жить поэтапные инвестиции. Например, строительство завода можно пред­ставить как последовательность реальных опционов, каждый из которых обусловлен предыдущим. На каждом этапе проект можно продолжить, вло­жив в него новую сумму денег (цена исполнения). И наоборот, на каждом этапе его можно прекратить, продав завод и выручив за него некую сумму Другие примеры такого рода опционов - программы НИОКР, внедрение на рынок новых продуктов, разведка и освоение нефтегазовых месторождений или программы поглощений, первоначальные инвестиции в которых мож­но рассматривать как базу для последующих поглощений.

«Арочные» опционы. Множественные источники неопределенности по­рождают так называемые «арочные» опционы. В частности, большинству программ НИОКР свойственны два типа неопределенности: связанная с тех-нологиями и связанная с рыночным успехом нового продукта. Последная воплощается в динамике цены продукта от сегодняшнего, более или менее определенного уровня к будущим неизвестным уровням, зависящим от об­щего состояния экономики, как и от многих других неведомых факторов Следовательно, неопределенность, связанная с рыночным успехом про­дукта, нарастает с течением времени. Технологическая неопределенность, напротив, со временем убывает, по мере того как исследования и ишьгтания все полнее выявляют свойства и возможности нового продукта. Такого же рода «арочный» опцион присутствует и в разведке/освоении природных ресурсов.

Нақты опциондарды бағалау әдістері.

В этом разделе мы сопоставим три метода принятия решений: оценку чистой приведенной стоимости, анализ дерева решений и модель оценки опционов. Кроме того, мы введем фундаментальную концепцию, на которой зиждется модель оценки опционов. Суть этой концепции, вкратце, заключается в том, что всегда можно подобрать дублирующий портфель из рыночных ценных бумаг, который дает такую же отдачу, как и опцион, а следовательно, имеет такую же рыночную стоимость. Эту концепцию иногда называют условием нулевого арбитража или законом единой цены - на основании того факта, что активы, приносящие одинаковую отдачу, должны также иметь одина­ковую цену в отсутствие арбитражных прибылей.

Возьмем для примера простой опцион на отсрочку. Предположим, у вас появилась возможность в конце года вложить 115 дол.в проект, который с равной вероятностью (50 на 50) принесет вам отдачу (денежный поток) в размере 170 или 65 дол. Безрисковая процентная ставка {rfiравна 8%. Среди обращающихся на рынке акций вы обнаружили «близнеца» вашего проекта, то есть бумагу, находящуюся с ним в совершенной корреляций, которая обеспечивает отдачу 34 или 13 дол.и продается по рыночной цене 20 дол. Заметьте, что отдача акции-вблизнеца» в любом случае составля­ет ровно пятую часть отдачи вашего проекта. Есть два способа оценить ваш проект с помощью акции-«близнеца». Во-первых, вы можете найти соответствующие этой акции затраты на капитал и использовать их для дисконтирования ожидаемого денежного потока проекта - традиционный подход. Затраты на капитал (k)вычисляются как ставка дисконтирования, уравнивающая приведенную стоимость (PV)ожидаемого денежного потока проекта [E(FCF)) с приведенной стоимостью акции-«близнеца»:

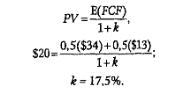
К оль скоро отдача акции-«близнеца» совершенно коррелирует с отдачей ва­шего проекта, ей должен быть свойствен и такой же риск, так что вы можетедисконтировать ожидаемый денежный поток проекта по той же скорректи­рованной на риск ставке 17,5%. Стало быть, стоимость проекта равна:

Второй способ — подобрать дублирующий портфель, то есть портфель рыночных ценных бумаг, чей денежный поток полностью воспроизводит денежный поток вашего проекта. Допустим, вы хотите составить дублирую­щий портфель из N акций-«близнецов» и безрисковых облигаций на В дол­ларов. При благоприятном стечении обстоятельств этот портфель принесет отдачу в размере 170 дол:

П ри скверном обороте событий портфель принесет отдачу 65 дол.:

Итак, у нас есть два уравнения с двумя неизвестными. Решения: N=5, В = 0. С такими решениями и при цене акции-«близнеца» 20 дол. приве­денная стоимость вашего проекта и дублирующего портфеля должна быть одинаковой:

Чистая приведенная стоимость проекта, если мы должны принимать реше­ние об инвестировании сегодня же, равна приведенной стоимости притока денежных средств (100 дол.) минус приведенная стоимость оттока денеж­ных средств (при определенном оттоке 115 дол.в следующем году, дискон­тированном по безрисковой ставке 8%, его приведенная стоимость равна -106,48 дол.):

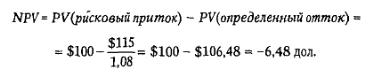
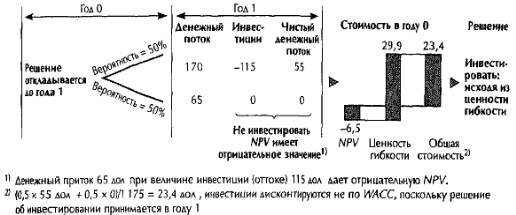
При условии, что мы должны прямо сейчас определиться, вкладывать ли нам деньги в конце года, наше решение будет отрицательным - не вклады­вать. Но ответ будет другим, если у нас есть опцион на отсрочку, позволя­ющий принять решение в следующем году, после того как мы воочию уви­дим, какой из двух возможных исходов осуществится в действительности. Прибегнув к анализу дерева решений, мы обнаружим (см. рис.3), что чистый денежный поток при благоприятном обороте событий составит 170 дол. -115 дол. = 55 дол., коль скоро мы решились инвестировать. При скверном обороте событий мы просто не станем инвестировать, так что чистый денежный поток будет нулевым.

П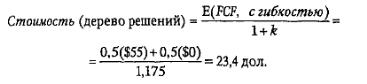 родисконтировав ожидаемыйденежный поток по затратам на капитал, получим оценку стоимости по методу дерева решений:

Стоимость опциона на отсрочку равна разности между оценочной стоимо­стью проекта, обладающего гибкостью, и стоимостью проекта в отсутствие гибкости: 23,4 дол. - (-6,5 дол.) = 29,9 дол.

Изъян метода дерева решений заключается в том, что мы используем здесь затраты на капитал, присущие базовому проекту в отсутствие гибко­сти, для оценки опциона на отсрочку, то есть реального опциона, который приносит другую отдачу и, соответственно, отличается другим риском, нежели базовый проект. В анализе дерева решений применяется ситуа­тивная (adhoc) ставка дисконтирования, не подходящая для оцениваемых рисковых денежных потоков.

Методология оценки опционов опирается на концепцию дублиру­ющего портфеля. Мы (как уже делали раньше) составляем портфель из Nакций-<6лизнецов» и безрискового займа (облигаций) на В долларов. При благоприятном обороте событий акции приносят отдачу по 34 дол. каждая, а облигации — номинальную стоимость, равную В дол., плюс про­центы в размере rjB. Общая отдача должна быть равна 55 дол. При небла­гоприятном обороте событий работает та же схема. В результате мы имеем два уравнения с двумя неизвестными:

Решения: N = 2,62, В = -31,53 дол. Стоимость проекта, обладающего гиб­костью в связи с опционом на отсрочку, равна:

Опционная стоимость = N*(цена акций-«близнецов») + В = 2,62($20) - $31,53 = 20,86 дол

Стоимость самого опциона на отсрочку равна разности между стоимостью проекта, обладающего гибкостью, и его стоимостью в отсутствие гибкости: 20,86 дол. - (-6,48 дол.) = 27,4 дол. Это корректная, свободная от арбитра­жа оценка. Соответствующая ей скорректированная на риск ставка дискон­тирования равна 31,9% (а не 17,5%):

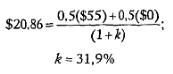
Риск опциона на базовый рисковый актив всегда выше, чем риск самого ба­зового актива. Проект в чистом виде имеет приведенную стоимость 100 дол. и равную вероятность (50 на 50) ее увеличения до 170 дол., то есть на 70%, или уменьшения до 65 дол., на 35%. Проект с опционом стоит 20,86 дол.» и его отдача с равной вероятностью возрастет до 55 дол., то есть на 164%, или окажется нулевой, то есть снизится на 100%. Этот повышенный риск объясняет, почему скорректированная на риск ставка дисконтирования для проекта с опционом составляет 31,9%.

Результаты этого сравнения обобщены на рисунке 4. Оценка NPVзанижает стоимость проекта, поскольку упускает ценность гибкости. Оценка методом дерева решений завышает ценность гибкости, поскольку в ней используется скорректированная на риск ставка дисконтирования, свойственная проекту, применительно к денежному потоку, сопряженному с опционом на отсрочку, — то есть к денежному потоку, который отличается гораздо более высоким риском.

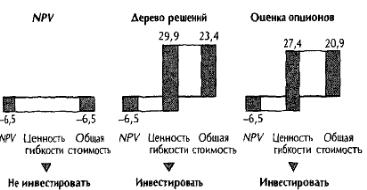
Модель оценки опционов дает верное значение стоимости, посколь­ку в ней надлежащим образом учитывается ценность гибкости — на ос­нове свободного от арбитража дублирующего портфеля. Но как найти акции-близнецы»? Мы можем принять за такие акции сам проект (в от­сутствие гибкости) и использовать его NPV(и отсутствие гибкости) в каче­стве рыночной цены, которой обладал бы проект, если бы действительно был представлен свободно обращающимися ценными бумагами. В конце концов, что может теснее коррелировать с проектом, чем сам этот проект? К тому же мы знаем, что приведенная стоимость (дисконтированный де­нежный поток) акций тесно коррелирует с их рыночной стоимостью, когда они не сопряжены ни с какими опционами. Чистая приведенная стоимость ожидаемого денежного потока проекта (в отсутствие гибкости) может слу­жить приемлемым показателем рыночной стоимости акций-вблизнецов». Будем называть такой подход отказом от рыночных активов.

Если мы берем в качестве акций-«близнецов» сам проект, то дублирую­щий портфель приносит следующую отдачу в благоприятных и неблагопри­ятных обстоятельствах (при безрисковой процентной ставке 8%):

N($170) + В(1 +rf)=55 дол.;

N($65) + В(1 +rf)= 0 дол.

Решив эти уравнения относительно неизвестных, находим:

N = 0,524; В = -31,53 дол.

При условии, что приведенная стоимость проекта (в отсутствие гибкости) составляет 100 дол., стоимость дублирующего портфеля равна стоимости проекта, обладающего гибкостью, а именно:

N($100) - $31.53 = 0,524(5100) - $31.53 = 20,86 дол

Мы не случайно получили ровно тот же ответ, как и при использовании действительных акций-«близнецов»: в обоих случаях присутствует совер­шенная корреляция исходов.

Қалыпты үлестірімдi компьютерлік үлгілеу.

Функции пакета Excel

Возвращает нормальную функцию распределения для указанного среднего и стандартного (среднеквадратичного) отклонения. Эта функция имеет очень широкий круг приложений в статистике, включая проверку гипотез.

Синтаксис: НОРМРАСП(x; Среднее; Стандартное_откл; Интегральная) где x - значение, для которого строится распределение, Среднее - среднее арифметическое распределения, Стандартное_откл - стандартное отклонение распределения, Интегральная - логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

Интегральная = 0 (ЛОЖЬ)	Интегральная = 1 (ИСТИНА)
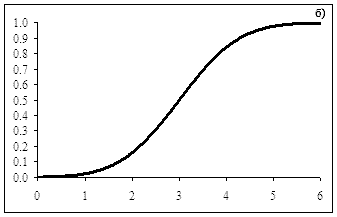
Рис. 1. Нормальное распределение со средним a = 3 и среднеквадратичным отклонением σ = 1. а) плотность вероятности p(x) для рассматриваемого нормального распределения; б) интегральная функция распределения F(x) = P(X < x). На рис. 1.а) выделена область соответствующая F(2) = P(X < 2). Эта область показывает вероятность того, что случайная величина X окажется меньше 2.

Еще одно пояснение к рисунку 1, синтаксису функции НОРМРАСП и понятию величины Интегральная: Нормальное распределение характеризуетнепрерывную случайную величину. Вероятность того, что значение X нормально расположенной случайной величины окажется меньше некоторой величины x равна F(x) = p(X<x). Эту зависимость F(x) и называют интегральной функцией нормального распределения. F(-∞) = 0; F(xср) = 0.5; F(+∞) = 1. Вид интегральной функции распределения для среднего равного 3 и среднеквадратичного отклонения, равного 1 приведен на рис. 1.б. Производная от интегральной функции распределения называется плотностью распределения:    (а).

Также верно и обратное: .   (б)

Плотность нормальной функции по определению равна .

Заметки: • Если Среднее или Стандартное_откл не является числом, то функция НОРМРАСП возвращает значение ошибки #ЗНАЧ!. • Если Стандартное_откл ≤ 0, то функция НОРМРАСП возвращает значение ошибки #ЧИСЛО!. • Если Среднее = 0, Стандартное_откл = 1 и Интегральная = ИСТИНА, то функция • НОРМРАСП возвращает стандартное нормальное распределение, то естьНОРМСТРАСП.

Уравнение для плотности нормального распределения (аргумент Интегральная содержит значение ЛОЖЬ) описывается функцией (а) и показано на рис. 1.а. Если аргумент Интегральная имеет значение ИСТИНА, формула описывает интеграл с пределами от «минус бесконечности» до «x» (см. (б) и рис. 1.б).

СССС

Субъективті және объективті ықтималдылықты реттеу.

Существуют понятия «объективная вероятность» и «субъективная вероятность». Первое включает в себя относительную частоту появления какого-либо события в общем объеме наблюдений (статистическое определение вероятности) или отношение числа благоприятных исходов к общему их количеству (классическое определение вероятности). Объективная вероятность определяется посредством анализа большого числа наблюдений, имевших место в прошлом. Под субъективной вероятностью понимают меру уверенности человека (эксперта) или группы людей в том, что данное событие в действительности будет иметь место. Её применяют тогда, когда невозможно воспользоваться объективной вероятностью по причине неполноты или отсутствия данных о наблюдениях в прошлом, из-за высокой стоимости получения объективной вероятности и др.Субъективную вероятность можно представить различными способами: распределением вероятностей и бинарным отношением на множестве событий, не полностью заданным распределением вероятностей или частичным бинарным отношением, и другими способами. Данную вероятность по форме представления разделяют на количественную и качественную. Количественная субъективная вероятность является вероятностной мерой на множестве событий, удовлетворяющей той же системе аксиом, что и вероятность объективная. С этой точки зрения она ничем не отличается от объективной вероятности. Разница заключается в используемых понятиях, поскольку числовые значения количественной субъективной вероятности формируются на основе мнений эксперта.

– объективное

ravg- сред.доход.

-общ доходность за весь период

n-количество

– стандартное отклонение доходности

σ - стандартное отклонение

r - средняя доходность CV коэффициент вариации

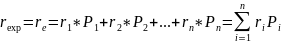– субъективное

r exp= ожидаемая норма доходности , r-доходность актива, Р-вероятность получения дохода

CV коэффициент вариации

ТТТТТ

Тиімді қоржындардын жиынтығы. Оңтайлы (қолайлы) қоржынын ұғымы.

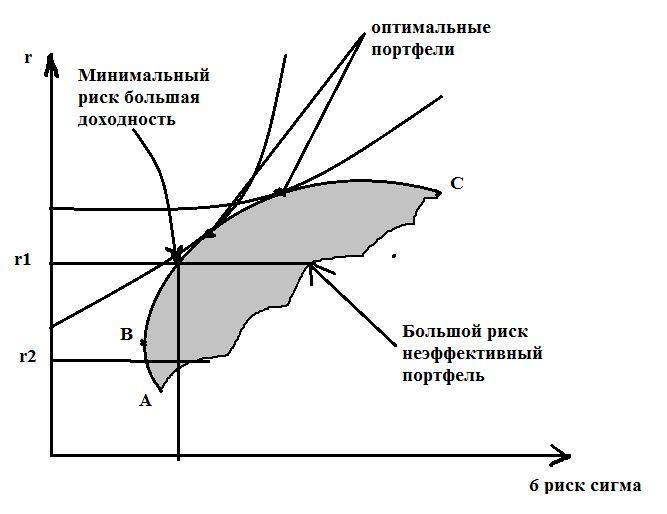
Эффективный портфель - портфель, обеспечивающий самую высокую ожидаемую доходность при заданном уровне риска, или, соответственно, самый низкий риск при заданной ожидаемой доходности.. Согласно подходу Г. Марковица, выбор портфеля инвестором основывается на ожидаемой доходности и стандартном отклонении. Осуществив оценку различных комбинаций портфелей, он выберет лучший по соотношению ожидаемой доходности и стандартного отклонения. Такой портфель будет эффективным портфелем, который обеспечит максимальную ожидаемую доходность для некоторого уровня риска, или минимальный уровень риска для некоторой ожидаемой доходности. Для нахождения эффективного портфеля акций необходимо рассчитать все допустимые множества портфелей (исходя из соотношения риск–доход) и отобразить границу, на которой будут лежать полученные портфели с минимальным риском при заданной доходности. Эффективная граница – это граница, которая определяет эффективное множество портфелей. Портфели, находящиеся слева от эффективной границы, выходят за границы допустимого множества, а значит, недопустимы к рассмотрению. Портфели, находящиеся справа и ниже эффективной границы, являются неэффективными, т.к. существуют портфели, которые при данном уровне риска обеспечивают более высокую доходность  либо более низкий риск для данного уровня доходности. Эффективная граница начинается с портфеля, который имеет минимальное значение стандартного отклонения (дисперсии). Портфели, лежащие на эффективной границе и находящиеся выше и правее эффективного портфеля, имеющего минимальный риск, также будут эффективными. 

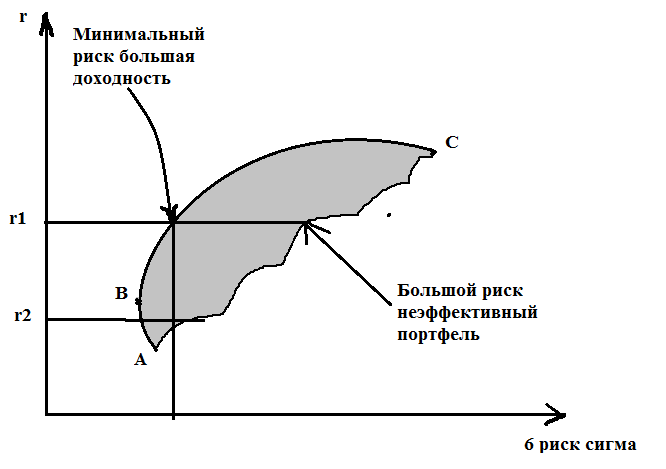
АВС – область допустимых портфелей

ВС-область эффективных портфелей

r2- вообще не эффективнй портфель потому что при таком уровне риска возможно получить больше доходности

Метод, применяемый при выборе оптимального портфеля, использует «кривые безразличия». Они отражают отношение инвестора к риску и доходности и могут быть представлены как график, на котором по горизонтальной оси откладываются значения риска, мерой которого является стандартное отклонение, а по вертикальной оси — величины вознаграждения, мерой которого служит ожидаемая доходность. Первое важное свойство кривых безразличия состоит в том, что все портфели, представленные на одной заданной кривой безразличия, равноценны для инвестора. Так, ему безразлично, какой актив выбрать А или В, поскольку оба они приносят ему одинаковую полезность. Более высокая ожидаемая доходность актива В компенсируется его более высоким риском. Аналогично инвестору безразлично, какой актив выбрать на второй кривой безразличия - С или D. В то же время кривые безразличия характеризуются тем, что любой портфель, который расположен на более высокой кривой безразличия, приносит инвестору большую ожидаемую полезность. Так активы С и D предпочтительнее для вкладчика по сравнению с активами Аи В. Второе важное свойство кривых безразличия: инвестор будет считать любой портфель, представленный на кривой безразличия, которая находится выше и левее, более привлекательным, чем любой портфель, представленный на кривой безразличия, которая находится ниже и правее.Число кривых безразличия бесконечно, т.е. как бы ни были расположены две кривые безразличия на графике, всегда существует возможность построить третью кривую, лежащую между ними. Также можно сказать, что каждый инвестор строит график кривых безразличия, представляющих его собственный выбор ожидаемых доходностей и стандартных отклонений. Поэтому инвестор должен определить ожидаемую доходность и стандартное отклонение для каждого потенциального портфеля и нанести их на график в виде кривых безразличия. Инвесторы, формируя портфель, стремятся максимизировать ожидаемую доходность своих инвестиций при определенном приемлемом для них уровне риска (и наоборот, минимизировать риск при ожидаемом уровне доходности). Портфель, удовлетворяющий этим требованиям, называется эффективным портфелем. Наиболее предпочтительный для инвестора эффективный портфель является оптимальным. Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых обеспечивает:

— максимальную ожидаемую доходность для некоторого уровня риска;

— минимальный риск для некоторого значения ожидаемой доходности.

Набор портфелей, удовлетворяющий этим двум условиям, называется эффективным множеством. Причем особую важность имеют портфели, находящиеся на границе этого множества.

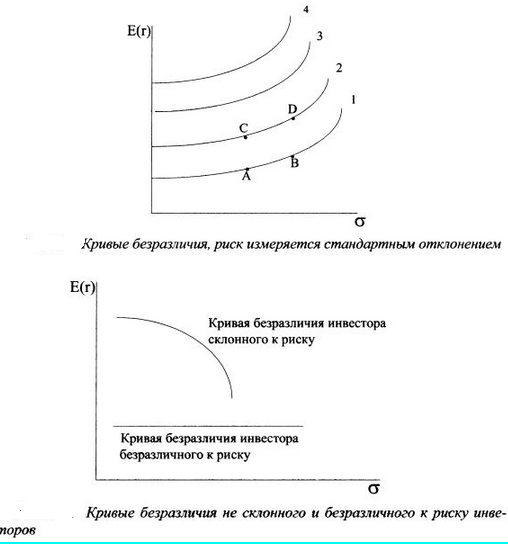
Когда кривая безразличия инвестора касается границы области эффективных портфелей точки соприкасания называются оптимальными портфелями. Акцияның ортақ тәуекел элементі.

Элементы общего риска акций — это две составляющие риска: 1) несистематический, или диверсифицируемый, риск, который присущ отдельным акциям и может быть устранен путем формирования эффективного портфеля; 2) систематический, или недиверсифицируемый, или рыночный, риск, который присущ всему рынку акций и не может быть устранен за счет формирования портфеля. 

– объективное

ravg- сред.доход.

-общ доходность за весь период

n-количество

– стандартное отклонение доходности

σ - стандартное отклонение

r - средняя доходность

CV коэффициент вариации

– субъективное

r exp= ожидаемая норма доходности , r-доходность актива, Р-вероятность получения дохода

CV коэффициент вариации

Общий риск акции имеряется дисперсией, дисперсией стандартного отклонения, коэф.вариации. (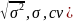

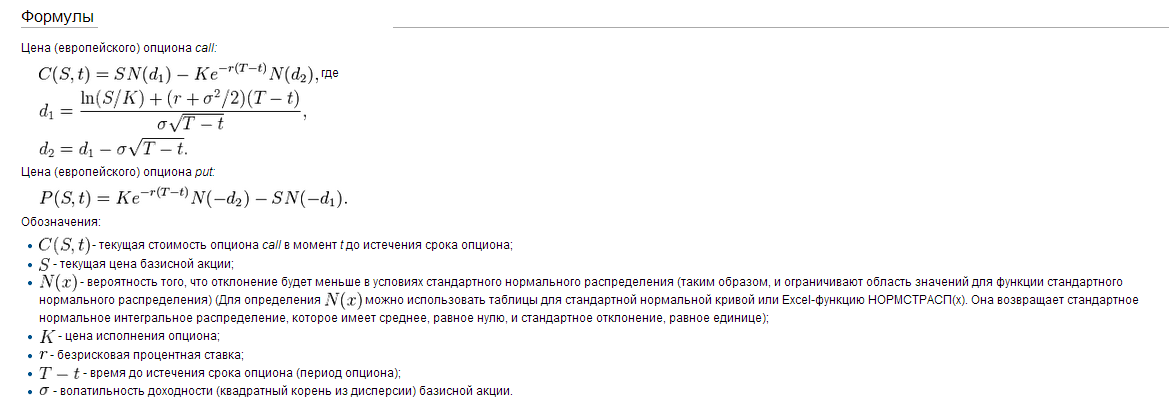
Блэк-Шоулздын опциондарды бағалау үлгісі.

Модель ценообразования опционов Блэка–Шоулза (англ. Black–Scholes Option Pricing Model, OPM) — это модель, которая определяет теоретическую цену на европейские опционы, подразумевающая, что если базовый актив торгуется на рынке, то цена опциона на него неявным образом уже устанавливается самим рынком. Данная модель получила широкое распространение на практике и, помимо всего прочего, может также использоваться для оценки всех производных бумаг, включая варранты, конвертируемые ценные бумаги, и даже для оценки собственного капитала финансово зависимых фирм.

Согласно Модели Блэка-Шоулза, ключевым элементом определения стоимости опциона является ожидаемая волатильность базового актива. В зависимости от колебания актива, цена на него возрастает или понижается, что прямопропорционально влияет на стоимость опциона. Таким образом, если известна стоимость опциона, то можно определить уровень волатильности ожидаемой рынком

Формула модели оценки опционов впервые была выведена Фишером Блэком и Майроном Шоулзом в 1973 году в статье «Оценка опционов и коммерческих облигаций» (The Pricing of Options and Corporate Liabilities). Их исследования основывались на предыдущих работах Джека Трейнора, Пола Самуэльсона, Джеймса Бонеса, Sheen T. Kassouf и Эдварда Торпа и разрабатывались в период быстрого роста опционной торговли.

Шесть допущений теории

Чтобы вывести свою модель ценообразования опционов, Блэк и Шоулз сделали следующие предположения:

По базисному активу опциона дивиденды не выплачиваются в течение всего срока действия опциона.

Нет транзакционных затрат, связанных с покупкой или продажей акции или опциона.

Краткосрочная безрисковая процентная ставка известна и является постоянной в течение всего срока действия опциона.

Любой покупатель ценной бумаги может получать ссуды по краткосрочной безрисковой ставке для оплаты любой части ее цены.

Короткая продажа разрешается без ограничений, и при этом продавец получит немедленно всю наличную сумму за проданную без покрытия ценную бумагу по сегодняшней цене.

Торговля ценными бумагами (базовым активом) ведется непрерывно, и поведение их цены подчиняется модели геометрического броуновского движения с известными параметрами.

Вывод модели основывается на концепции безрискового хеджирования. Покупая акции и одновременно продавая опционы call на эти акции, инвестор может конструировать безрисковую позицию, где прибыли по акциям будут точно компенсировать убытки по опционам, и наоборот.

Безрисковая хеджированная позиция должна приносить доход по ставке, равной безрисковой процентной ставке, в противном случае существовала бы возможность извлечения арбитражной прибыли и инвесторы, пытаясь получить преимущества от этой возможности, приводили бы цену опциона к равновесному уровню, который определяется моделью.

Оперативтік және қаржылық леверидж