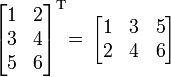30. Иммунизация сызбалары
Иммунизация портфеля облигаций
Одним из приемов пассивного управления портфелем является его иммунизация. Главный риск в отношении облигаций состоит в возможности изменения процентной ставки и, соответственно, цены облигации. Если менеджер стремится застраховаться от изменения стоимости портфеля облигаций к определенному моменту времени, то он должен сформировать его таким образом, чтобы дюрация портфеля соответствовала требуемому периоду времени. Тогда в случае изменения процентной ставки потери (выигрыши) в стоимости облигаций будут компенсироваться выигрышами (потерями) от реинвестирования купонов. Рассмотрим технику иммунизации вначале на примере портфеля, в который входит одна облигация.
Пример 1.
Номинал облигации 1000 руб., купон 10%, выплачивается один раз в год, время до погашения четыре года. Процентная ставка одинакова для всех периодов времени и равна 10% годовых, т.е. кривая доходности параллельна оси абсцисс на графике кривой доходности. Предполагается, что в случае изменения процентных ставок в течение времени обращения облигации кривая доходности будет смещаться параллельно. Купоны, получаемые по облигации, реинвестируются под текущий процент.
Дюрация Маколея облигации равна 3,49 года. Это означает, что, если инвестор купит облигацию по текущей цене и продаст через 3,49 года, то он обеспечит по инвестициям в облигацию доходность 10% годовых, независимо от того, как будут изменяться процентные ставки на рынке. Данный факт проиллюстрирован расчетами, приведенными в таблице 5.1.
В таблице приведены три варианта конъюнктуры на рынке. В третьей колонке представлена ситуация, когда процентная ставка оставалась неизменной в течение всех последующих четырех лет. От реинвестирования купонов под данную ставку до момента продажи облигации через 3,49 года и продажи облигации в это время инвестор в сумме получил 1394,63 руб. В четвертой колонке показано, что за первый год обращения облигации процентная ставка выросла на 1 % и оставалась неизменной в течение следующих трех лет. Поэтому все расчеты сделаны на основе 11%. В сумме инвестор получил 1394,72 руб. В пятой колонке конъюнктура соответствует случаю, когда в течение первого года ставка упала на 1% и оставалась неизменной на протяжении оставшегося времени. В итоге инвестор получил 1394,64 руб.
Таким
образом, на момент времени равный дюрации
облигации инвестор обеспечивает себе
сумму денег порядка 1395 руб. независимо
от изменения процентных ставок на рынке
в течение обращения облигации. Данная
сумма денег соответствует доходности
в 10% годовых, так как инвестор купил
облигацию за 1000 руб. и получил через
3,49 года 1394,6 руб.:
или
10%.
ҚҚҚҚҚ
Қаржыда матрицалық алгебраны қолдану.
Современному экономисту необходима серьёзная математическая подготовка — это положение общепризнано. К числу наиболее важных для экономистов областей математики относится статистика. В свою очередь статистические технологии полностью базируются на матричной алгебре. Применение матриц не только позволяет продуктивно формализовать поставленную проблему, но также использовать в расчётах многие достижения матричной алгебры. Отметим, что практически все многомерные методы статистического анализа можно детально изучить с помощью аппарата матричной алгебры. Типичным примером этого может служить регрессионный анализ. На этой же базе развиты и такие методы, как дискриминантный анализ, метод канонических корреляций и т.д. Изложение материала в данной книге ведётся на очень доступном и понятном уровне, в т.ч. для тех, кто далёк от математики. Данное пособие будет полезно не только экономистам, но и медикам, биологам, социологам, психологам и т.д. Все излагаемые в книге темы сопровождаются многими примерами, решение которых подробно комментируется. Матричная алгебра Матричная алгебра тесно связана с линейными функциями и с линейными ограничениями, в связи, с чем находит себе применение в различных экономических задачах: · в эконометрике, для оценки параметров множественных линейных регрессий; · при решении задач линейного программирования; · при макроэкономическом программировании и т.д. Особое отношение к матричной алгебре в экономике появилось после создания моделей типа «Затраты-Выпуск», где с помощью матриц технологических коэффициентов объясняется уровень производства в каждой отрасли через связь с соответствующими уровнями во всех прочих отраслях. Электронная таблица EXCEL имеет ряд встроенных функций для работы с матрицами: ТРАНСП транспонирование исходной матрицы; МОПРЕД вычисление определителя квадратной матрицы; МОБР вычисление матрицы обратной к данной; МУМНОЖ нахождение матрицы, являющейся произведением двух матриц. Кроме того, возможно выполнение операций поэлементного сложения (вычитания) двух матриц и умножения (деления) матрицы на число. На примере проиллюстрируем некоторые из этих функций. Найдем сумму двух матриц А(5*4) и В(5*4) и транспонируем матрицу-результат.
Все это проводилось в Екселе.
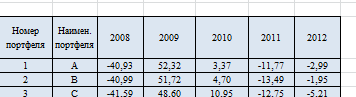
14 компаний от А-N 5 лет
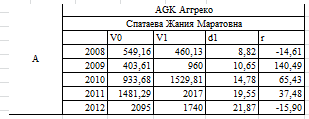
V0 |
цена закрытия на начало года |
V1 |
цена закрытия на конец года |
d1 |
дивиденды |
r |
доходность |
r вычисляется по формуле (V1+d1-V0)/V0*100
и так в каждой компании (14) мы нашли доходности за 5 лет.
Далее находим сумму среднее значение за один год. (А+B+…M)/13 (за отсутствием одного портфеля, в нашем случае N), и так формируем 13 портфелей.
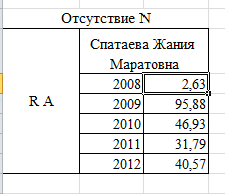
Н
аходим
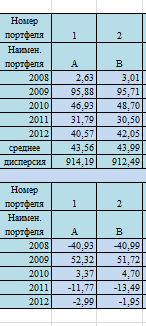
среднее значение (СРЗНАЧ) и дисперсию
ДИСП.Г) 2008-2012 г. далее матрицу избыточной
доход. Значение каждого года – среднее
число.
Далее мы воспользовались функцией ТРАНСП
Выделяем область куда должна переместится таблица в вертик виде, нажимаем функцию ТРАНСП , выдедяем таблицу с данными , нажимаем клавиши Сtrl* shift* enter. После того как мы вставили данные мы копируем таблицу, и вставляем используя при при этом специальную вставку – значения и ок. Затем убираем #Н/Д таким способом. Нажимаем CTRL – H . Найти #* Заменить на ничего не указываем и ок.
Далее мы вычислили дисперсионно ковариационную матрицу используя фунцию МУМНОЖ. Массив 1 – диапазон чисел уже транспонированной таблицы Массив 2 таблицу которую мы транспонировали (изначальную) и делим на количество лет.
Далее составляем таблицу удельный вес каждого портвеля 1/13 , в сумме удельные веса должны давать единицу. Далее мы воспользовались функцией ТРАНСП.
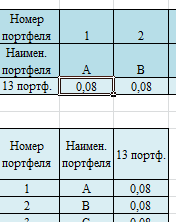
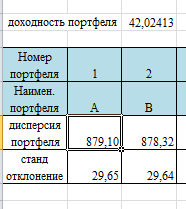
Потом с помощью функции МУМНОЖ нашли доходность портфеля (данные среднее значение портфел.и транспонированный удельный вес.
Далее нашли дисперсию портфеля МУМНОЖ (таблица с удельными весами и таблица с ковар.дисперсионной матрицей)и стандартное отклонение функция КОРЕНЬ (Дисперсия портфеля).
Матрицалық алгебраны қолданумен портфелдің тәуекелінің автономдық тәуекелді бөліп алу алгоритімі.
МММММ
Мол табыстардың матрицасын тасымалдау.
Рассмотрим 2 ценные бумаги А и В. Для начала необходимо составить матрицу избыточных доходностей. Где строки матрицы – это избыточные доходности по годам, а столбцы матрицы – избыточные доходности по конкретной ценной бумаге.
|
А |
В |
1 |
ra1-raсреднее |
rb1-rbсреднее |
2 |
ra2-raсреднее |
rb2-rbсреднее |
3 |
ra3-raсреднее |
rb3-rbсреднее
|
Доходность по данным бумагам находится по формуле: ra1=(Va1+d-Va0)/Va0, где Va1- стоимость бумаги на конец года; d-дивиденд за 1 год; Va0 – стоимость бумаги на начало года. Также находится ra2, ra3 и по бумаге В.
Потом находим среднюю доходность: raсреднее=(ra1+ra2+ra3)/3
Далее можно транспонировать эту матрицу:
|
1 |
2 |
3 |
A |
ra1-raсреднее |
ra2-raсреднее |
ra3-raсреднее |
B |
rb1-rbсреднее |
rb2-rbсреднее |
rb3-rbсреднее
|
Взаимосвязь между ними проявляется в том, что строки одной матрицы являются столбцами другой. В то время как первая матрица имеет размер 2:3, размер второй матрицы 3:2. Когда матрицы связаны подобным образом, то говорят, что каждая из них является транспонированной матрицей относительно другой. Например, В есть транспонированная матрица А, а А – транспонированная матрица В.
Транспонирование матриц удобно проводить в Excel с помощью функции ТРАНСП.
Составление матрицы избыточных доходностей и потом ее транспонирование необходимо для того, чтобы их потом перемножить и найти дисперсионно-ковариационную матрицу портфеля ценных бумаг и определить риск портфеля.
МУМНОЖ(массив1;массив2)
Массив1, массив2 — массивтердің көбейтіндісі.
МУМНОЖ функциясында сандарды ғана еңгіземіз. Столбецтердің саны массив 1 строктардың саны массив 2 санына тең болу керек Егер саныңыз дұрыс шықпаса онда, МУМНОЖ функциясы значение ошибки #ЗНАЧ, деп шығарады
Массивтің өлшемі 5 461 ячейкаға тең болуы керек
i —строктардың номері, j —столбецтердің номері.
Мысал 1
Создайте пустую книгу или лист.
Выделите пример в разделе справки. Не выделяйте заголовок строки или столбца.
Выделение примера в справке.
Нажмите сочетание клавиш CTRL+C
На листе выделите ячейку A1 и нажмите сочетание клавиш CTRL+V.
Чтобы переключиться между просмотром результатов и просмотром формул, возвращающих эти результаты, нажмите сочетание клавиш CTRL+` (апостроф) или в меню Сервис укажите на пункт Зависимости формул и выберите режим Режим проверки формул.
|
|
Бұл жерде массивтің формуласын қолдану керек Диапоз А8:В9выделяем клавища F2 , басамыз, содан кейін CTRL+SHIFT+ENTERСан 2 ге тең болуы керек
Мол табыстылықтардың матрицасын модельдеу
Мол табыстылықтардың матрицасын модельдеуді есептеу кезінде мынандай формулалар қолданылады:
Екі реттік мол табыстылықты есептеу
Мол табыстылық матрицаның суммасы
Мол табыстылықтардың матрицасын модельдеу мысалында
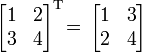и
