Билет № 20

1. Решение задачи линейного программирования графическим методом.

2. Решить систему линейных уравнений методом Гаусса:

4. В таблице приведены данные (в условных единицах) о наличии трудовых ресурсов на предприятии по каждому из типов ресурсов, о трудоёмкости изготовления единицы продукции каждого вида с разбивкой по типам трудовых ресурсов, а также о цене единицы продукции каждого вида:

Тип трудовых ресурсов	Трудоёмкость единицы продукции				Наличие трудовых ресурсов
	А	Б	В	Г
1	2	1	3	2	300
2	1	1	4	5	150
3	3	4	2	1	130
Цена единицы продукции	4	8	5	6

3. Составить начальный опорный план и проверить его на оптимальность

Билет № 21

1. Решение задачи линейного программирования симплекс-методом с естественным базисом.

2. Найти базисные решения системы уравнений, указать, какие из них являются допустимыми:

3. Составить двойственную задачу к прямой задаче: mах f(х) = 4х₁ + 2х₂

х₁ - 3х₂ ≥ -9

2х₁ + 3х₂ ≤ 18

2х₁ - х₂ ≤ 10

х_1,2≥ 0.

Найти оптимальный план этой задачи на основе первой и второй теорем двойственности

линейного программирования, если оптимальный план прямой задачи Х* = (6; 2)

Билет № 22

1. Построение двойственной задачи линейного программирования.

2. Найти матрицу, обратную к матрице: А =

3. Найти базисные решения системы уравнений, указать, какие из них являются допустимыми:

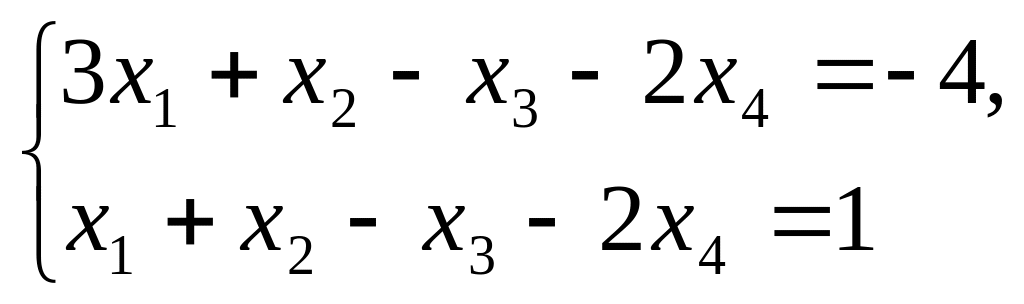
Билет № 23

1. Экономическая интерпретация двойственной задачи.

2. Решить систему уравнений методом обратной матрицы

3. Решите графическим методом задачу линейного программирования. Найдите минимум функции f(х) при заданных ограничениях: f(х) = х₁ - 2х₂

х₁ - 4х₂ ≥ -8

х₁ - 2х₂ ≤ 2

2х₁ + 3х₂ ≥ 6

х_1,2≥ 0

Билет № 24

1. Связь между оптимальными планами пары двойственных задач.

2. Проверить равенство 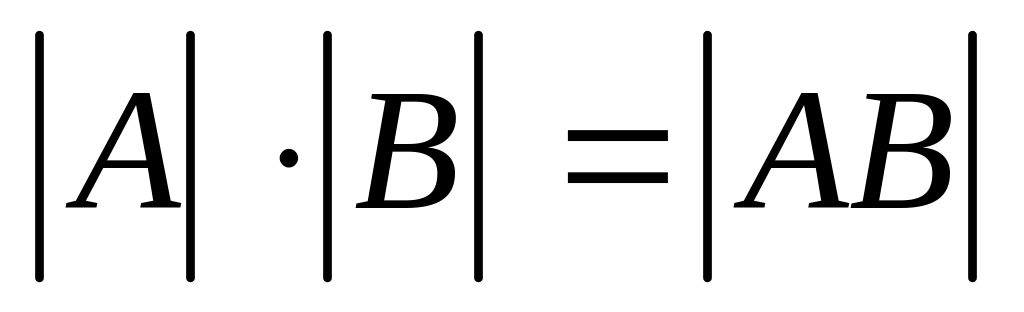, если

3. Записать двойственную задачу к исходной задаче: min f(х) = 2х₁ - 3х₃

2х₁ - х₂ ≤ -4

х₁ + х₂ ≥ 5

х_1,2≥ 0

Билет № 25

1. Решение систем линейных уравнений методом Гаусса.

2. Решить уравнение:

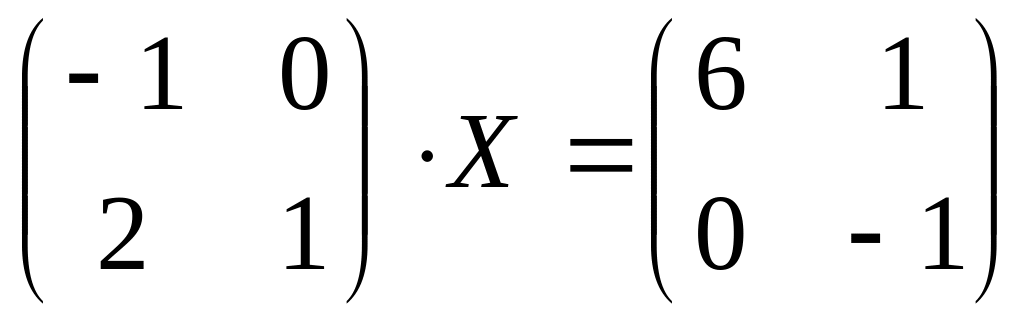
3. Составить двойственную задачу к прямой задаче: mах f(х) = 3х₁ + 2х₂

х₁ - 4х₂ ≥ -8

х₁ - 2х₂ ≤ 2

2х₁ + 3х₂ ≥ 6

х_1,2≥ 0.

Найти оптимальный план этой задачи на основе первой и второй теорем двойственности

линейного программирования, если оптимальный план прямой задачи Х* = (12; 5)