Билеты к экзамену по дисциплине «Математика»

3 курс, специальность «Менеджмент»

Преподаватель – Карпункова Г. Н.

Билет № 1

1. Определение матрицы. Виды матриц.

2. Решить систему линейных уравнений по формулам Крамера:

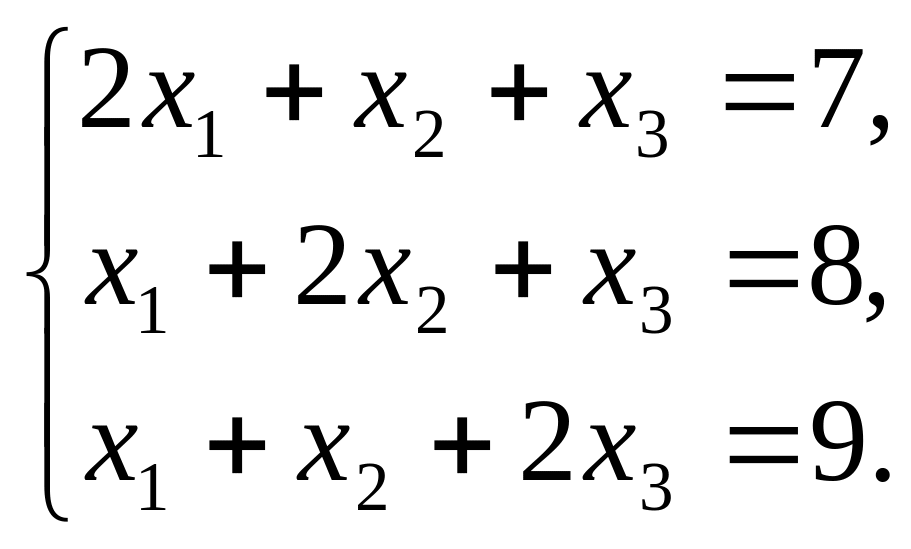
3. В таблице приведены данные (в условных единицах) о наличии трудовых ресурсов на предприятии по каждому из типов ресурсов, о трудоёмкости изготовления единицы продукции каждого вида с разбивкой по типам трудовых ресурсов, а также о цене единицы продукции каждого вида:

Тип трудовых ресурсов	Трудоёмкость единицы продукции				Наличие трудовых ресурсов
	А	Б	В	Г
1	2	1	3	2	200
2	1	2	4	8	160
3	2	4	1	1	170
Цена единицы продукции	5	7	3	6

Сформулировать исходную оптимизационную задачу оптимального использования трудовых ресурсов на максимум общей стоимости выпускаемой продукции и привести её к каноническому виду.

Билет № 2

1. Алгебраические операции над матрицами. Транспонирование матриц.

2. Найти решения системы

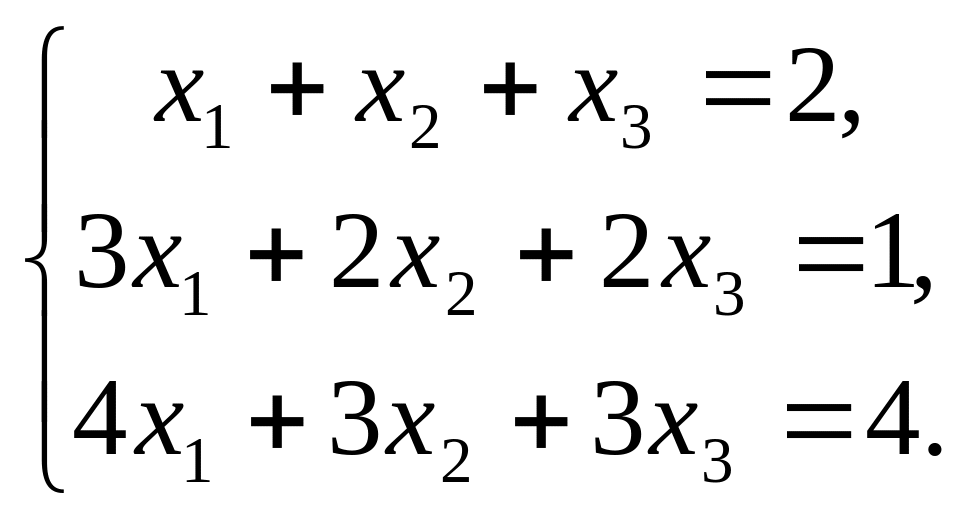
3. Проверить на оптимальность начальный опорный план и построить новый опорный план

Номер симплекс-таблицы	Базис	с j сi	План В	5	7	3	6	0	0	0	Q
				А1	А2	А3	А4	А5	А6	А7
0	А5	0	200	2	1	3	2	1	0	0
	А6	0	160	1	2	4	8	0	1	0
	А7	0	170	2	4	1	1	0	0	1

Билет № 3

1. Определители первого, второго и третьего порядков. Вычисление определителей.

2. Решить систему уравнений методом Гаусса:

3. Для производства продукции типа П₁ и П₂ предприятие использует два вида сырья: С₁ и С₂. Данные об условиях приведены в таблице:

Сырьё	Расход сырья на единицу продукции, кг/ед.		Количество сырья, кг
	П1	П2
С1	1	3	300
С2	1	1	150
Прибыль, тыс. руб./ед. прод.	2	3	-

Составить план производства по критерию «максимум прибыли». Решение выполнить симплекс-методом.

Билет № 4

1. Свойства определителей.

2. Указать способы и число разбиений переменных системы

на основные и неосновные.

3. Записать двойственную задачу к исходной задаче: «Найдите максимум функции

f(х) = 4х₁ - 3х₂ при заданных ограничениях:

х₁ + 2х₂ ≥ 2

2х₁ + х₂ ≤ 10

х₁ - х₂ ≤ 1

х_1,2≥ 0»

Билет № 5

1. Минор и алгебраическое дополнение элемента матрицы n-го порядка.

2. Найти базисные решения системы уравнений

3. Записать двойственную задачу к исходной задаче: «Найдите минимум функции f(х) = -4х₁ + 6х₂ при заданных ограничениях:

х₁ + 2х₂ ≥ 5

4х₁ - х₂ ≤ 10

х₁ + х₂ ≤ -6

х_1,2 ≥ 0.»

Билет № 6

1. Теорема Лапласа.

2. Решить уравнение: АХ = 2В², где

3. Решит задачу графическим методом.

Найдите минимум функции f(х) = 4х₁ - 3х₂ при заданных ограничениях:

х₁ + 2х₂ ≥ 2

2х₁ + х₂ ≤ 10

х₁ - х₂ ≤ 1

х_1,2≥ 0

Билет № 7

1. Присоединённая и обратная матрицы.

2. Найти базисные решения системы уравнений

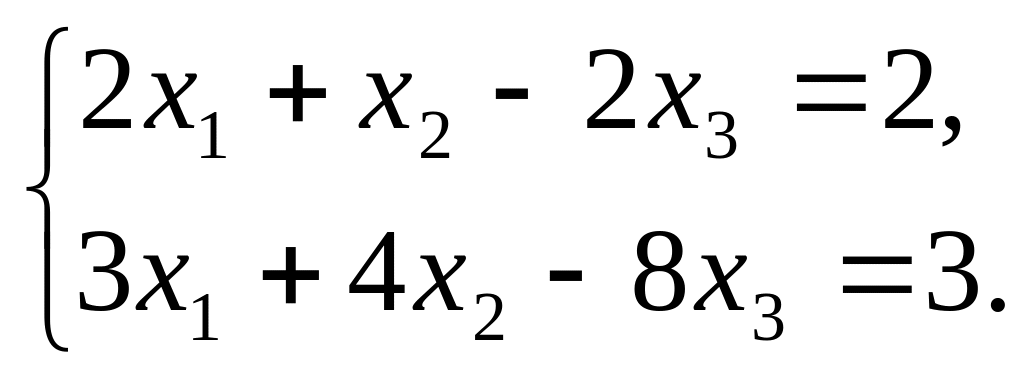
3. В таблице приведены данные (в условных единицах) о наличии трудовых ресурсов на предприятии по каждому из типов ресурсов, о трудоёмкости изготовления единицы продукции каждого вида с разбивкой по типам трудовых ресурсов, а также о цене единицы продукции каждого вида:

Тип трудовых ресурсов	Трудоёмкость единицы продукции				Наличие трудовых ресурсов
	А	Б	В	Г
1	2	1	3	2	200
2	1	2	4	8	160
3	2	4	1	1	170
Цена единицы продукции	5	7	3	6

Составить начальный опорный план и проверить его на оптимальность.

Билет № 8

1. Алгоритм вычисления обратной матрицы.

2. Решить систему уравнений по формулам Крамера

3. Решите графическим методом задачу линейного программирования. Найдите максимум и минимум функции f(х) = 4х₁ - 3х₂ при заданных ограничениях:

х₁ + 2х₂ ≥ 2

2х₁ + х₂ ≤ 10

х₁ - х₂ ≤ 1

х_1,2≥ 0

Билет № 9

1. Система m линейных уравнений с n переменными (общий вид). Однородные и неоднородные системы.

2. Дана матрица 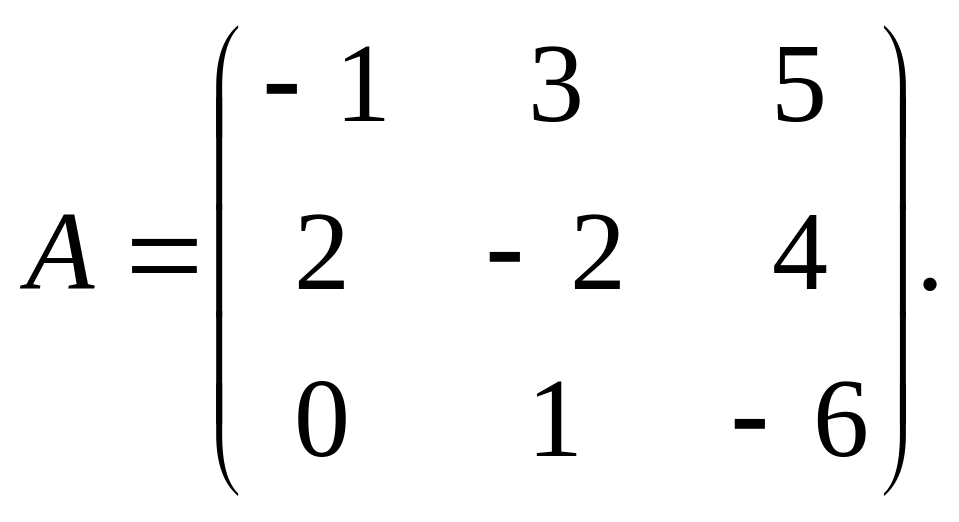Какую матрицу В нужно прибавить к матрице А, чтобы получить единичную матрицу?

3. Сформулировать исходную оптимизационную задачу оптимального использования трудовых ресурсов на максимум общей стоимости выпускаемой продукции и решить её симплексным методом:

Тип трудовых ресурсов	Трудоёмкость единицы продукции			Наличие трудовых ресурсов
	А	Б	В
1	1	2	1	430
2	3	0	2	460
3	1	4	0	420
Цена единицы продукции	3	2	5

Билет № 10

1. Матрица системы m линейных уравнений с n переменными (m > n). Матричная форма записи системы.

2. Найдите матрицу С = 2А – В ^/, если

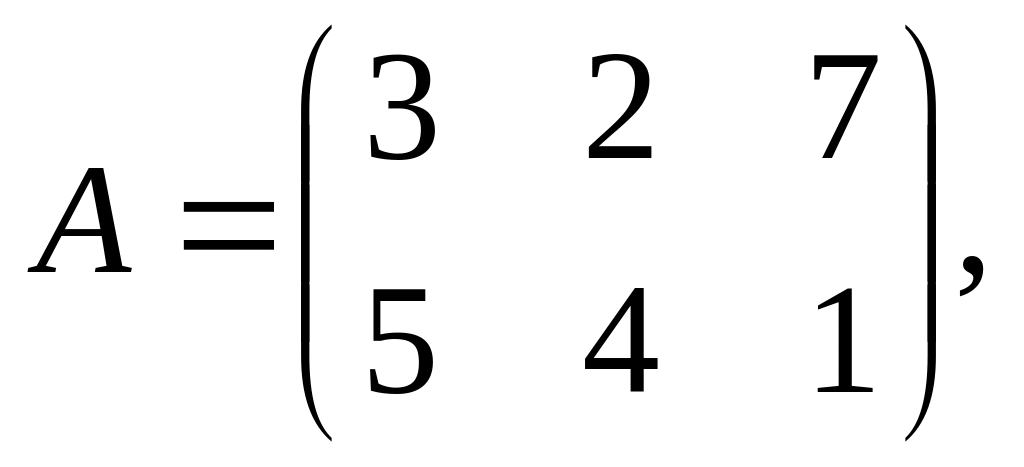
3. Решите графическим методом задачу линейного программирования. Найдите максимум f(х) = 3х₁ + 2х₂ при заданных ограничениях:

х₁ - 4х₂ ≥ -8

х₁ - 2х₂ ≤ 2

2х₁ + 3х₂ ≥ 6

х_1,2≥ 0

Билет № 11

1. Совместные (определённые и неопределённые) и несовместные системы.

2. Вычислить определитель, воспользовавшись теоремой Лапласа:

3. Решите графическим методом задачу линейного программирования. Найдите минимум функции f(х) при заданных ограничениях: f(х) = х₁ - 2х₂

х₁ - 4х₂ ≥ -8

х₁ - 2х₂ ≤ 2

2х₁ + 3х₂ ≥ 6

х_1,2≥ 0

Билет № 12

1. Правило Крамера для решения квадратной системы линейных уравнений.

2. Даны матрицы 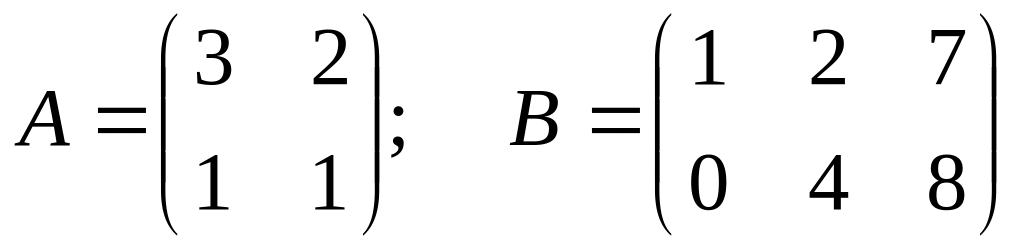. Решить уравнение АХ = В.

3. Записать двойственную задачу к исходной задаче: mах f(х) = х₁ + х₂ + 2х₃

2х₁ + х₂ + х₃ ≤ 15

-2х₂ - 3х₃ ≤ -10

х₁ + х₂ + 4х₃ = 8

х_1,2≥ 0

Билет № 13

1. Метод исключения неизвестных - метод Гаусса.

2. Найти матрицу, присоединенную к матрице

3. Решите графическим методом задачу линейного программирования. Найдите максимум функции f(х) = -х₁ + х₂ при заданных ограничениях:

х₁ - 2х₂ ≥ -2

х₁ + х₂ ≤ 10

х₁ - 3х₂ ≤ 6

х_1,2≥ 0

Билет № 14

1. Решение системы линейных уравнений методом обратной матрицы.

2. Даны матрицы . Решить уравнение ХА = С.

3. Решите графическим методом задачу линейного программирования. Найдите максимум и минимум функции f(х) = 10х₁ + 5х₂ при заданных ограничениях:

2х₁ - 3х₂ ≤ 6

х₁ + 2х₂ ≥ 4

4х₁ + х₂ ≥ 1

х_1,2≥ 0

Билет № 15

1. Система m линейных уравнений с n переменными(m < n).

2. Дана матрица 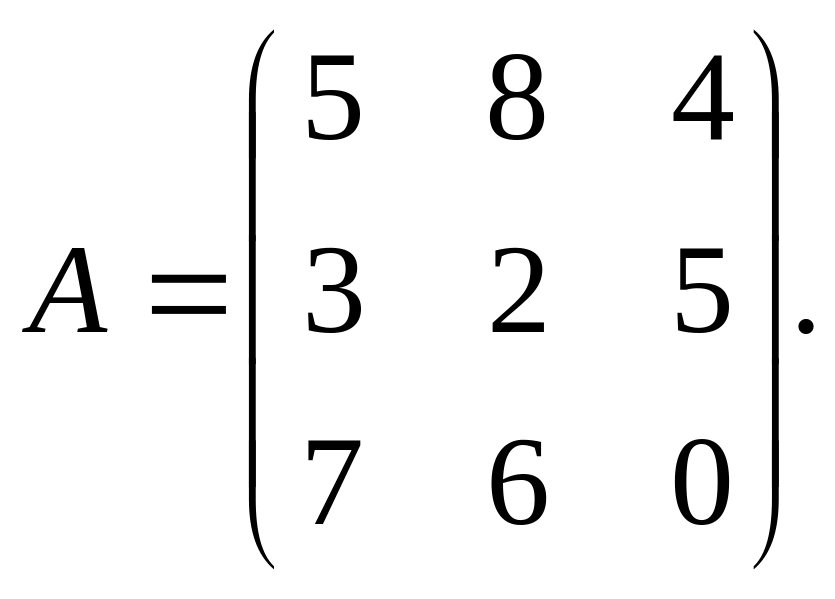Какую матрицу В нужно прибавить к матрице А, чтобы получить единичную матрицу?

3. Сформулировать исходную оптимизационную задачу оптимального использования трудовых ресурсов на максимум общей стоимости выпускаемой продукции и решить её симплексным методом:

Тип трудовых ресурсов	Трудоёмкость единицы продукции			Наличие трудовых ресурсов
	А	Б	В
1	4	2	1	180
2	3	1	3	210
3	1	2	5	244
Цена единицы продукции	10	14	12