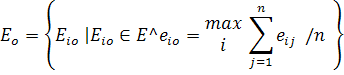Міністерство освіти і науки України
Національний лісотехнічний університет України
Кафедра АВП Е і Т
Розрахункова робота №1
Обгрунтування прийняття рішень за умов невизначеності
Виконав: ст. гр. Л-51м
Федорич М.С.
Перевірив:
Мисик М. М.
Львів-2014
Таблиця1.1 Завдання
|
k1 |
k2 |
k3 |
k4 |
k5 |
k6 |
xi |
10 |
30 |
50 |
70 |
90 |
110 |
20 |
0 |
14 |
28 |
42 |
56 |
70 |
30 |
-4,7 |
23,3 |
51,3 |
79,3 |
107,3 |
135,3 |
40 |
-21 |
21 |
63 |
105 |
147 |
189 |
50 |
-84 |
-28 |
28 |
84 |
140 |
196 |
1. Критерій Вальда (обережного спостерігача) оптимізує корисність за припущення, що середовище знаходиться в найбільш невигідному для спостерігача стані:
− для кожного рядка (стратегії/рішення) обирають мінімальне значення корисності: 0;-47;-21;-84;
− з обраних корисностей обирають максимальне значення (0), яке і є вирішенням проблеми, бо визначає продуктивність Xопт = 20.
Але від придбання обладнання слід відмовитися, якщо керуватися критерієм Вальда, бо корисність/прибуток є нульою величиною (Іопт = 0).
Таблиця 1.2. Визначення оптимальної корисності виробничого обладнання в умовах невизначеності за критерієм Вальда
|
k1 |
k2 |
k3 |
k4 |
k5 |
k6 |
Критерій Вальда |
xi |
10 |
30 |
50 |
70 |
90 |
110 |
|
20 |
0 |
14 |
28 |
42 |
56 |
70 |
0 |
30 |
-4,7 |
23,3 |
51,3 |
79,3 |
107,3 |
135,3 |
-4,7 |
40 |
-21 |
21 |
63 |
105 |
147 |
189 |
-21 |
50 |
-84 |
-28 |
28 |
84 |
140 |
196 |
-84 |
Оптимальна корисність 0 при використанні обладення з продуктивністю 20
|
|||||||
Критерій Вальда обумовлює варіант рішення співвідношенням:
2. Критерій Лапласа. Оскільки ймовірність виникнення тієї чи іншої ситуації невідома, будемо, вважати, що всі вони рівноймовірні. Тоді для кожного рядка матриці виграшів розраховується середнє арифметичне значення оцінок. Із отриманих середніх величин оптимальним вважається максимальне значення, яке і дозволяє визначити продуктивність обладнання. Максимальне значення корисності lmax = 60, звідки оптимальна продуктивність X3 = 140 див. табл.1.3.
Таблиця 1.3. Визначення оптимальної корисності виробничого обладнання в умовах невизначеності за критерієм Лапласа
|
k1 |
k2 |
k3 |
k4 |
k5 |
k6 |
Критерій Лапласа |
xi |
10 |
30 |
50 |
70 |
90 |
110 |
|
20 |
0 |
14 |
28 |
42 |
56 |
70 |
35 |
30 |
-4,7 |
23,3 |
51,3 |
79,3 |
107,3 |
135,3 |
65,3 |
40 |
-21 |
21 |
63 |
105 |
147 |
189 |
84 |
50 |
-84 |
-28 |
28 |
84 |
140 |
196 |
56 |
Оптимальна корисність 84 при використанні обладення з продуктивністю 40 |
|||||||
Критерій Лапласа обумовлює варіант рішення співвідношенням:
