3.2.1 Определение количества путей в сетевой модели
Количество путей в данной сети определяется от исходного события до завершающего.
Например: пути 0-1-6-7, 0-3-5-7, 0-2-4-7 и др.
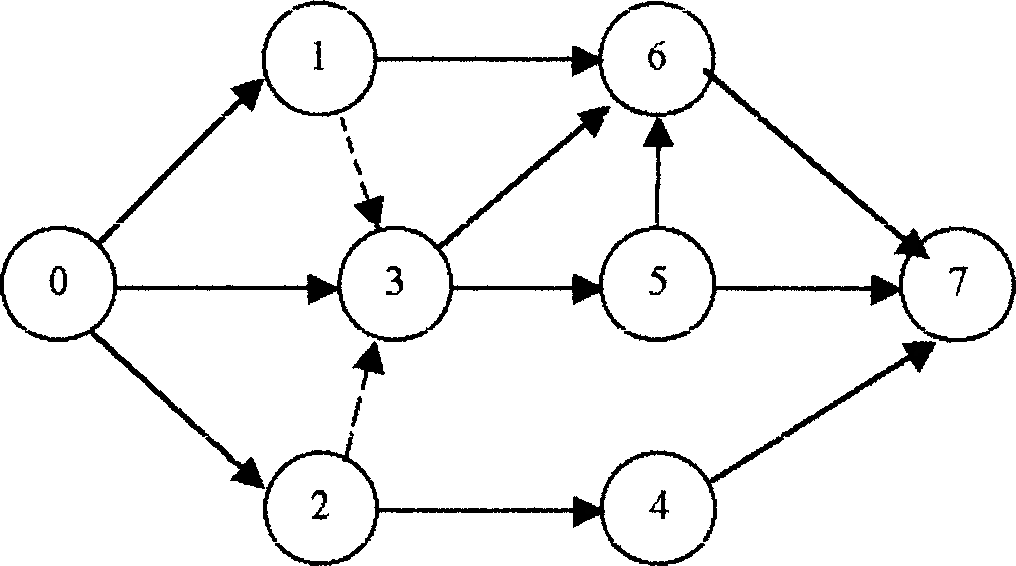
Рисунок 3.12
В данной сети 11 путей.
4. Оптимизация сетевого графика
При оптимизации анализируются структура графика, трудоемкость и длительность выполнения каждой работы, вероятность завершения разработок в заданный срок и загрузка исполнителей.
Анализ сетевого графика предусматривает также выравнивание коэффициентов напряженности работ Knij:
,
где
(28)
- продолжительность
максимального пути, проходящего через
данную работу (дни);
- продолжительность
отрезка пути
,
совпадающего с критическим путем (дни).
При анализе сетевых графиков производится расчет вероятности свершения завершающего события в данный срок Тд , при этом чаще всего учитывают работы только критического пути, используя закон нормального распределения tij, то есть
,
где
(29)
– аргумент
нормальной функции распределения
вероятностей;
- срок свершения
завершающего события (по расчету в
днях);
- сумма дисперсий
работ, лежащих на критическом пути.
Найдя Z по таблице значений функции Лапласа, определяют вероятность свершения завершающего события в заданный срок.
Таблица 4 – Значения функций Лапласа
Z |
Pk |
Z |
Pk |
Z |
Pk |
Z |
Pk |
0.0 |
0.5000 |
1.6 |
0.9452 |
-0.3 |
0.0013 |
-1.4 |
0.0808 |
0.1 |
0.5398 |
1.7 |
0.9554 |
-2.9 |
0.0019 |
-1.3 |
0.0968 |
0.2 |
0.5793 |
1.8 |
0.9641 |
-2.8 |
0.0026 |
-1.2 |
0.1151 |
0.3 |
0.6179 |
1.9 |
0.9713 |
-2.7 |
0.0035 |
-1.1 |
0.1357 |
0.4 |
0.6554 |
2.0 |
0.9772 |
-2.6 |
0.0047 |
-1.0 |
0.1587 |
0.5 |
0.6915 |
2.1 |
0.9821 |
-2.5 |
0.0062 |
-0.9 |
0.1841 |
0.6 |
0.7257 |
2.2 |
0.9861 |
-2.4 |
0.0082 |
-0.8 |
0.2119 |
0.7 |
0.7580 |
2.3 |
0.9893 |
-2.3 |
0.0107 |
-0.7 |
0.2420 |
0.8 |
0.7881 |
2.4 |
0.9918 |
-2.2 |
0.0139 |
-0.6 |
0.2743 |
Продолжение таблицы 4
0.9 |
0.8159 |
2.5 |
0.9938 |
-2.1 |
0.0179 |
-0.5 |
0.3085 |
1.0 |
0.8413 |
2.6 |
0.9953 |
-2.0 |
0.0228 |
-0.4 |
0.3446 |
1.1 |
0.8643 |
2.7 |
0.9965 |
-1.9 |
0.0287 |
-0.3 |
0.3821 |
1.2 |
0.8849 |
2.8 |
0.9974 |
-1.8 |
0.0359 |
-0.2 |
0.4207 |
1.3 |
0.9032 |
2.9 |
0.9981 |
-1.7 |
0.0446 |
-0.1 |
0.4602 |
1.4 |
0.9192 |
3.0 |
0.9987 |
-1.6 |
0.548 |
-0.0 |
0.5000 |
1.5 |
0.9332 |
|
|
-1.5 |
0.0668 |
|
|
Распределение ресурсов (исполнителей) по срокам работ определяют путем построения «карты проекта» или графика потребности в исполнителях.
Расчеты при оптимизации сетевых графиков проводятся вручную или на вычислительных машинах. При оптимизации графика с неограниченными ресурсами стремятся к тому, чтобы на работах критического и подкритического путей объем ресурса (число исполнителей) точно соответствовал потребности их для выполнения разработки в заданный срок.
При графическом методе оптимизации можно применять ряд способов. На примере рассмотрим один из способов оптимизации графиков при ограниченных ресурсах.
Пример. Необходимо оптимизировать сетевой график (рисунок 4.1) по времени выполнения при ограниченном ресурсе исполнителей 10 человек. Для простоты принят один вид исполнителей - конструкторы. Над стрелками (работами) дана продолжительность работы, а под стрелкой (в квадрате) - число исполнителей. Для решения задачи используется график Ганта в следующей последовательности:
1. Составляются линейная диаграмма и график ежедневной потребности ресурса - карта проекта (рисунок 4.2).График Ганта строится следующим образом. На ось абсцисс наносится равномерная шкала времени t, каждая работа изображается полоской, параллельной оси абсцисс, длиной, равной продолжительности работы. Фиктивные работы снизу вверх одна над другой в порядке возрастания индекса работы j. Работы на линейной диаграмме указывают по ранним срокам свершения событий.
2. По графику Ганта очень быстро и просто определяется t(Lкр), Рпij.
3. По графику ежедневной потребности, изображенной на карте проекта, видно, что в 4, 5, 6, 9, 10-й дни недостает конструкторов, тогда как в 7, 8, 11, 12, 13 и дни и дальше имеется резерв в конструкторах.
4. Рассматривается первый участок до окончания одной из работ - 1 и 2-й дни - и анализируется возможность передвинуть вправо некоторые работы. Применяется следующая очередность оставления работ на данном участке:
1) работы критического пути;
2) работы, не законченные в предыдущем периоде;
3) работы в последовательности уменьшения полного резерва. При этом учитываются также фронт и коэффициенты напряженности работ.
Работу 0,2 передвигать нельзя, так как она лежит на критическом пути;
работа 0,1 имеет полный резерв, равный 7 дням; работа 0,3 имеет свободный резерв 4 дня.
По правилу необходимо передвинуть вправо работу 0,1 , как имеющую наибольший резерв. Но в данном случае лучше передвинуть вправо начало работы 0,3 на 3 дня, так как на работе 0,1 занято большее число исполнителей.
5. Строятся (изменяется старая) диаграмма и график ежедневной потребности ресурса (рисунок 4.3).
6. Анализируется следующий участок графика, т. е. от оптимизированного участка до окончания работы критического пути - 4, 5 и 6-й дни. Из графика видно, что в 4, 5 и 6-й дни не хватает конструкторов.
Анализируются работы, попадающие на этот участок времени. Работа 2, 3 находится на критическом пути, остальные работы имеют полные резервы;
работа 0,3 - 1 день; 1,4-7 дней; 1,5 - 11 дней.
Передвинув вправо с участка 4, 5, 6-го дней работы 1,4 и 1,5 и следующие за ними работы 4,8 и 5,8 получают распределение, работ, удовлетворяющее именующемся ресурсу (рисунок 4.4).
Последовательно рассматривая каждый участок, можно достичь соблюдения заданных условий (сроков, числа исполнителей).
Обратная задача, т. е. оптимальное распределение ресурсов при ограниченном времени выполнения проекта, проводится также по линейным диаграммам, но при этом работы рассматриваются в обратной последовательности.
При наличии нескольких видов ресурсов проводится оптимизация по каждому и выбирается наиболее оптимальный вариант.
Может быть поставлена задача и другого типа – снизить стоимость разработки за счет увеличения продолжительности работ, имеющих резервы времени, или наоборот – минимизировать время разработки, допустив увеличение стоимости.
Исследуя зависимости между продолжительностью и стоимостью работ, устанавливают их оптимальное соотношение для рассматриваемого варианта разработки.
Для каждого вида работ необходимо построить график время – затраты
(рисунок 4.5), характеризующийся наклоном аппроксимирующей кривой. Пользуясь такими графиками, можно определить величину затрат Сі, необходимых для выполнения работы в сокращенное время:
(30)
или степень нарастания затрат в единицу времени:
(31)
В этих формулах Сп – повышенные денежные затраты при выполнении работы в минимально возможное время Тm; Сm – затраты при выполнении работы в нормальное время Тн; Тс – время, в которое предполагается выполнить работу.
Если при оптимизации изменилась длительность критического пути и оценка по времени работ, а также, если изменился директивный срок совершения завершающего события, необходимо еще раз рассчитать Рк.
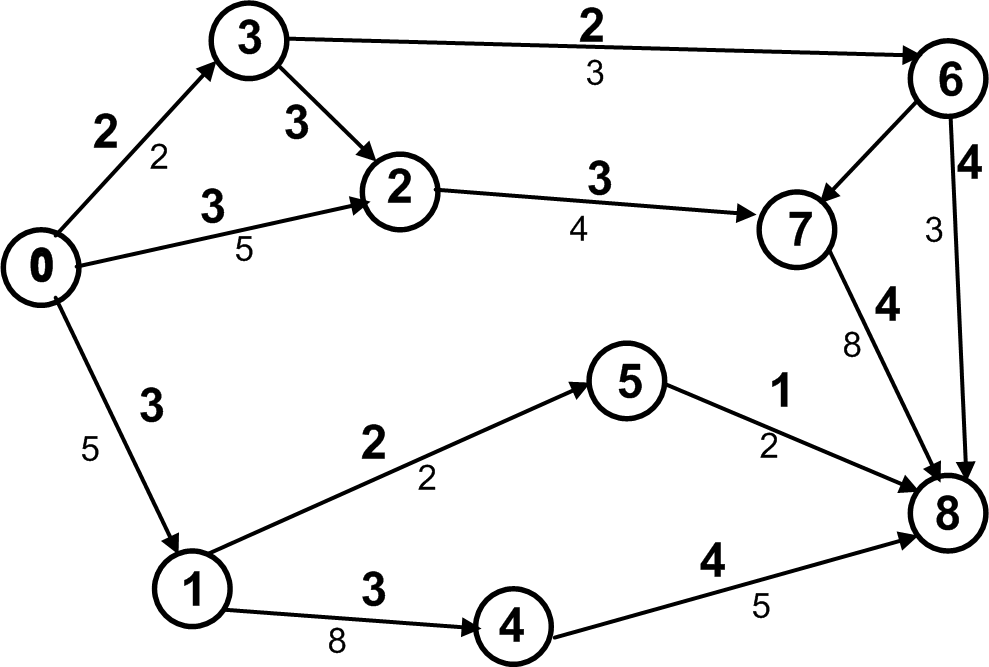
Рисунок 4.1
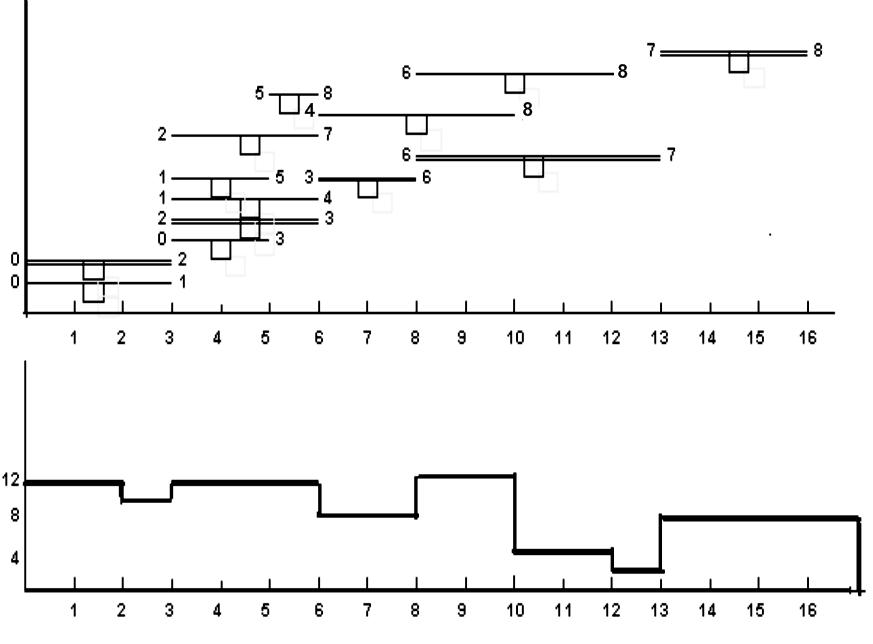
Рисунок 4.2 – Ленточная диаграмма, карта проекта
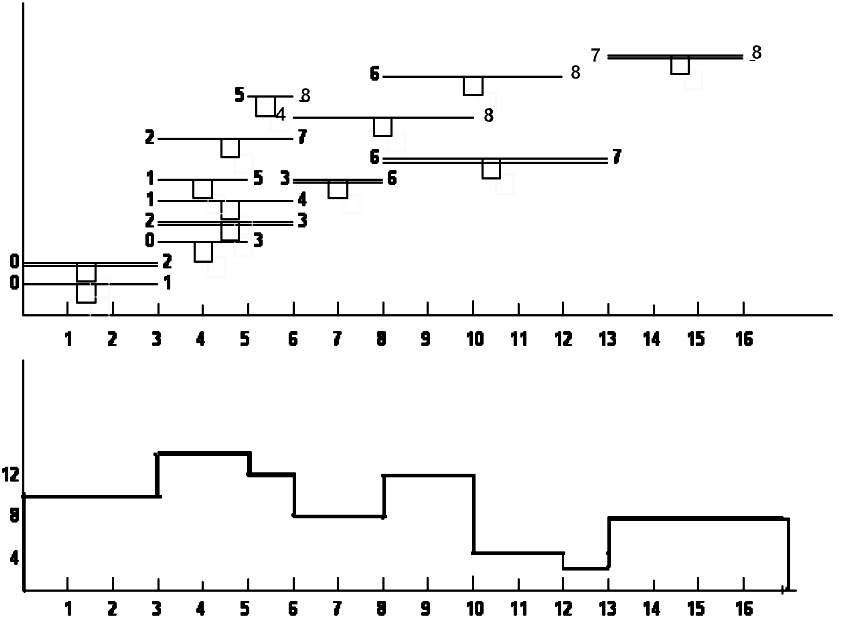
Рисунок 4.3 – Диаграмма и график ежедневной потребности ресурсов
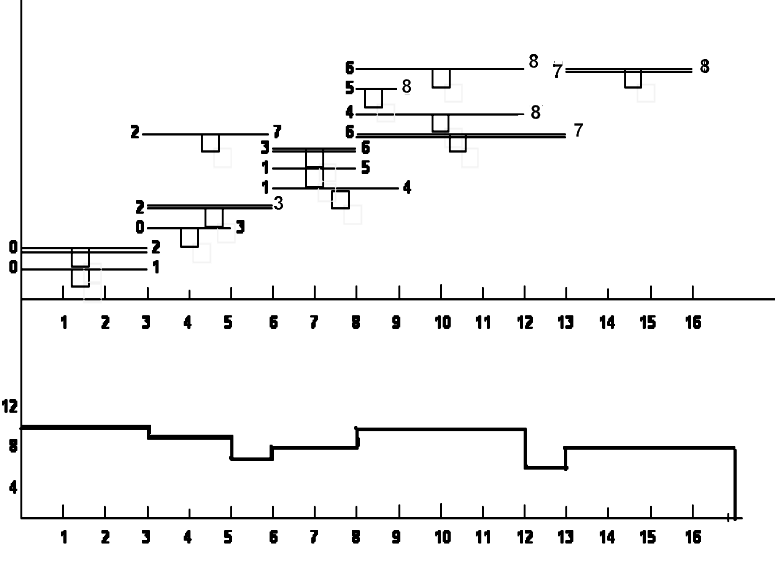
Рисунок 4.4 – Диаграмма ленточного графика и карты проекта
Представим обобщающий график «Время - затраты», которые расходуются на проект (Рис. 4.5).
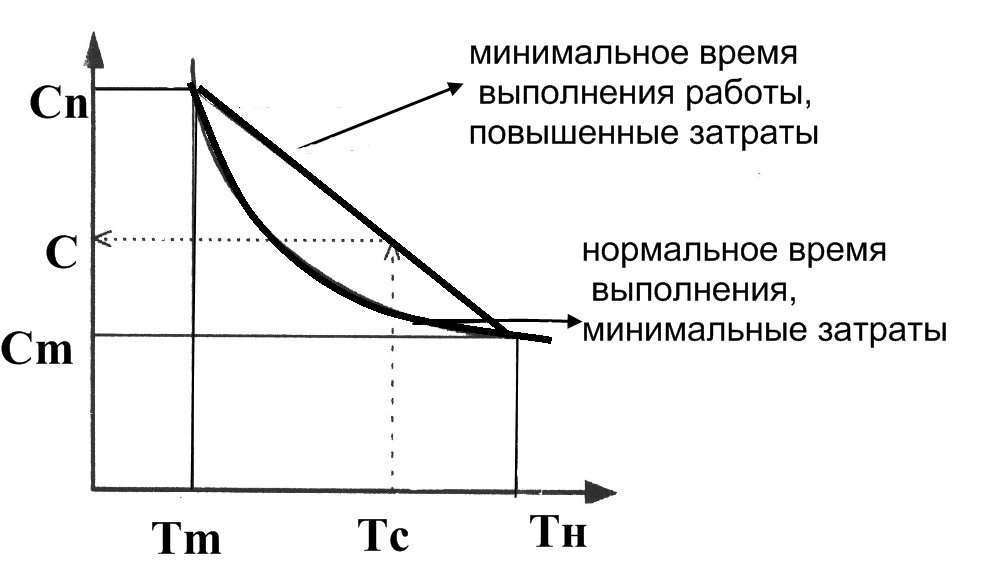
Рисунок 4.5 – График «Время - затраты»