9. Методы оценки измерений

Измерения являются основной составной частью любого эксперимента. От тщательности измерений и последующих вычислений зависят результаты эксперимента. Поэтому каждый экспериментатор должен знать закономерности измерительных процессов: уметь правильно измерить изучаемые величины; оценить погрешности при измерениях; правильно, с требуемой точностью вычислить значения величин и их минимальное количество; определить наилучшие условия измерений, при которых ошибки будут наименьшими, и произвести общий анализ результатов измерений.

Измерение – это процесс нахождения какой-либо физической величины опытным путем с помощью специальных технических средств, это познавательный процесс сравнения величины чего-либо с известной величиной, принятой за единицу (эталон).

Теорией и практикой измерений занимается специальная наука – метрология.

Измерения бывают статическими, когда измеряемая величина не изменяется, и динамическими, когда она меняется (например, измерение пульсирующих процессов).

Кроме того, измерения разделяются на прямые и косвенные.

При прямых измерениях искомую величину устанавливают непосредственно из опыта, при косвенных – функционально от других величин, определенных прямыми измерениями: , где – величина, найденная с помощью косвенных измерений, – с помощью прямых измерений.

Различают три класса измерений

1. Особо точные – эталонные измерения с максимально возможной точностью. Этот класс почти не применяется в экспериментальных исследованиях.

2. Высокоточные – измерения, погрешность которых не должна превышать заданных значений. Этот класс измерений используют при некоторых наиболее ответственных экспериментах, а также для контрольно-поверочных измерений приборов.

3. Теоретические измерения, в которых погрешность определяется особенностями средств измерения.

Различают абсолютные и относительные измерения.

Погрешность измерения – это алгебраическая разность между действительным значением измеряемой величины и полученным при измерении

Измерение – это такое значение измеряемой величины, которое заведомо точнее, чем получаемое при измерении. С некоторым допущением можно считать истинным или точным значением величины.

Значение иногда называют абсолютной ошибкой измерения.

Относительная ошибка измерения

. (116)

Точность измерения – это точность приближения измерения к действительному значению величины.

Достоверность измерения показывает степень доверия к результатам измерения, т.е. вероятность отклонений измерения от действительных значений.

Чтобы повысить точность и достоверность измерений, необходимо уменьшить погрешности. Погрешности при измерениях возникают вследствие ряда причин: несовершенства методов и средств измерений; недостаточно тщательного проведения опыта; влияния различных внешних факторов в процессе опыта, субъективных особенностей экспериментатора и др. Эти причины являются результатом действия многих факторов.

Погрешности классифицируют на систематические и случайные.

Систематические – это такие погрешности измерений, которые при повторных экспериментах являются постоянными (или изменяются по известному закону). Если численные значения этих погрешностей известны, их можно учесть во время повторных измерений.

Случайными называют погрешности, возникающие чисто случайно при повторном измерении. Эти измерения не могут быть исключены, как систематические. Однако при наличии многократных повторностей с помощью статистических методов можно исключить наиболее отклоняющиеся случайные измерения.

Разновидностью случайных погрешностей являются грубые погрешности или промахи, существенно превышающие систематические или случайные погрешности. Промахи и грубые погрешности вызваны, как правило, ошибками экспериментатора. Их легко обнаружить. В расчет эти погрешности не принимаются и при вычислении их исключают. Таким образом, можно записать

, (117)

где – систематические и случайные погрешности измерений.

В процессе эксперимента трудно отделить систематические погрешности от случайных. Однако при тщательном и многократном эксперименте все же можно исключить систематические погрешности (ошибки). Основная задача измерений заключается в том, чтобы получить по возможности результаты измерений с меньшими погрешностями. Ниже рассмотрены основные принципы и методы устранения систематических и случайных ошибок.

Систематические погрешности можно разделить на пять групп.

1 группа – инструментальные погрешности, возникающие вследствие нарушений средств измерений: дополнительных люфтов или трения, неточности градуированной шкалы, износа и старения узлов и деталей.

2 группа – погрешности, которые возникают из-за неправильной установки средств измерений.

3 группа – погрешности, возникающие в результате действия внешней среды: высоких температур, воздуха, магнитных и электрических полей, атмосферного давления и влажности воздуха, вибрации и колебаний от движущегося транспорта и др.

4 группа – субъективные погрешности, возникают вследствие индивидуальных физиологических, психофизиологических, антропологических свойств человека.

5 группа – погрешности метода, которые появляются в результате необоснованного метода измерений (при различных упрощениях схем или функциональных зависимостей, при отсутствии теоретических обоснований метода измерения, малом количестве повторностей и др.).

Систематические погрешности могут быть постоянными или переменными, увеличивающимися и уменьшающимися в процессе эксперимента. Их обязательно нужно исключать. Известны случаи, когда из-за наличия систематических погрешностей делались неправильные научные выводы из эксперимента. Систематические ошибки (погрешности) могут быть устранены следующими методами.

Часто от систематических погрешностей 1 – 5 групп можно избавиться до начала эксперимента путем регулировки или ремонта средств измерения, тщательной проверки установки средств измерений, устранения нежелательных воздействий, внешней среды. Особое внимание должно быть уделено обоснованию теории и методики измерений. Одним из эффективных методов устранения систематических ошибок 1 –3 групп является исключение их в процессе эксперимента. Основным принципом этого исключения является повторное измерение. При измерении вместо исследуемого объекта устанавливают эталонированный, заранее измеренный с высокой точностью. Разность в измерениях позволит найти погрешность измерительного средства.

Если все же нельзя установить значения систематических погрешностей, то ограничиваются оценкой их границ.

Случайные погрешности. При проведении с одинаковой тщательностью тех или иных экспериментов результаты измерений одной и той же величины (даже с учетом известного закона систематических погрешностей), как правило, отличаются между собой. Как отмечалось выше, это свидетельствует о наличии случайных погрешностей.

Каждый экспериментатор, анализируя результаты измерений, должен уметь правильно оценить неизбежно возникающие случайные погрешности. К случайным ошибкам относятся также, как уже известно, промахи и грубые погрешности.

Наиболее типичными причинами промахов являются ошибки при наблюдениях: неправильный отсчет по шкале измерительных приборов, описки (ошибки) при записи результатов измерений, различные манипуляции с приборами или их отдельными узлами (перестановка, замена блоков, проверка и др.). Грубые погрешности возникают вследствие неисправности приборов, а также внезапно изменившихся условий эксперимента.

Анализ случайных погрешностей основывается на теории случайных ошибок. Эта теория дает возможность с определенной гарантией вычислить действительное значение и оценить возможные ошибки, по которым судят о действительном значении искомой величины.

В основе теории случайных ошибок лежат предположения о том, что при большом числе измерений случайные погрешности одинаковой величины, но разного знака, встречаются одинаково часто, что большие погрешности встречаются реже, чем малые, или вероятность появления погрешности уменьшается с ростом ее величины; что при бесконечно большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерений; что появление того или иного результата измерения как случайного события описывается нормальным законом распределения, если число измерения больше 30, или распределением Стьюдента, если количество измерений меньше 30.

Различают генеральную и выборочную совокупность измерений. Под генеральной совокупностью измерений подразумевают все множество возможных значений измерений или возможных значений погрешностей . Для выборочной совокупности измерений величина ограничена, и в каждом конкретном случае строго определяется. Обычно считают, что если > 30, то среднее значение данной совокупности измерений достаточно приближается к его истинному значению.

Теория случайных ошибок позволяет решить две задачи: оценить точность и надежность измерения при данном количестве замеров, определить минимальное количество замеров, гарантирующее требуемую (заданную) точность и надежность измерения.

Рассмотрим первую задачу при большом количестве измерений, > 30. Разброс показателей (однородность) измерения характеризуется величиной дисперсии и показателем вариации (изменчивости) :

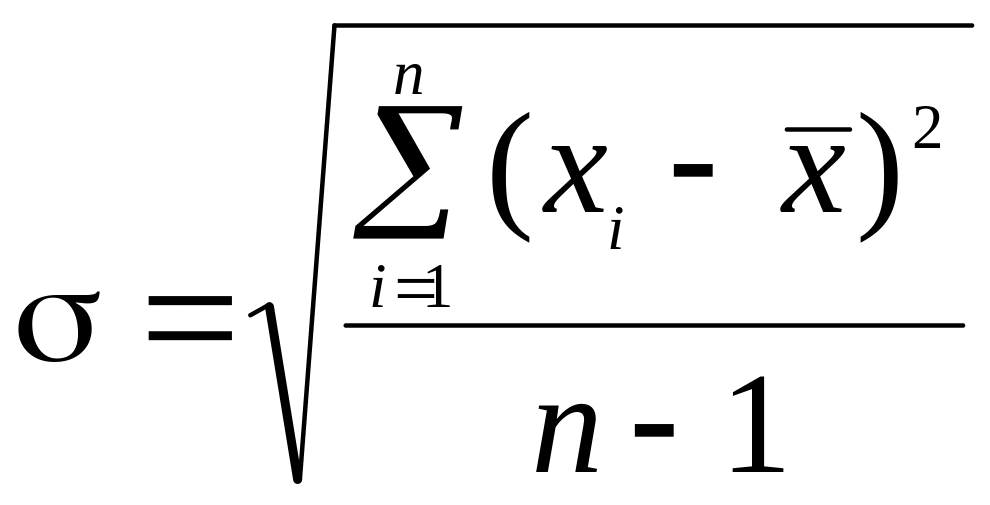; . (118)

Чем больше и , тем больше разброс показателей измерений. Зная величины и , можно определить доверительный интервал и доверительную вероятность (надежность) измерения.

Доверительным интервалом называется интервал значений , в который попадает истинное значение измеряемой величины с заданной вероятностью. Доверительной вероятностью (надежностью) измерения называется вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал. Эта величина определяется в долях единицы или в процентах.

Обычно доверительный интервал определяют по формуле:

, (119)

где – гарантийный коэффициент ).

Доверительная вероятность, гарантийный коэффициент и значение связаны соотношением

(120)

Функцию называют интервалом вероятностей или интервалом Лапласа. Численные значения интервала вероятности приведены в литературе.

Величину называют уровнем значимости. Из нее следует, что при нормальном законе распределения погрешность, превышающая доверительный интервал, будет встречаться один раз из измерений:

(121)

Или иначе приходится браковать одно из измерений.

Зная величины , можно дать характеристику качества измерения.

Пример. Допустим, испытано 53 образца породы. Определено, что средняя прочность при сжатии Па.

Задаваясь величиной , можно определить доверительный интервал и доверительную вероятность измерения по таблице. Так, при Па, т.е. Па. Из таблицы определим доверительную вероятность Значит, из 1000 измерений 683 попадает в данный доверительный интервал, а 317 результатов выходят за его пределы.

При Па, т.е. Па.

По таблице , следовательно, из 1000 измерений 993 попадают в данный доверительный интервал и только 3 измерения выходят за его пределы.

При выполнении измерений необходимо знать их точность , которую обычно характеризуют величиной – среднеарифметическое значение среднеквадратичного отклонения :

; . (122)

Величину часто называют средней ошибкой. Доверительный интервал ошибки точности измерения определяется аналогично, как и для величины измерений: . По величине легко определить доверительную вероятность (надежность) точности (ошибки) измерения из таблицы.

В исследованиях часто по заданной точности и доверительной вероятности (надежности) измерения определяют минимальное количество измерений, гарантирующих требуемые величины и . Для этой цели в большинстве случаев используют приближенную зависимость:

. (123)

В относительных величинах (123) принимает вид

. (124)

Здесь – коэффициент вариации (изменчивости), %;

– точность измерений, %.

Для вычисления может быть принята следующая последовательность.

1. Проводят предварительный эксперимент с количеством измерений , которое составляет в зависимости от трудоемкости опыта от 20 до 50.

2. Вычисляют среднеквадратичное отклонение (118).

3. В соответствии с поставленными задачами эксперимента устанавливают требуемую точность измерений, которая должна быть не менее точности прибора.

4. Устанавливают нормированное отклонение , величину которого обычно задают; она зависит также от точности метода. Например, при большой точности измерений и трудоемком эксперименте можно принять при малой – Так, измеряя влажность грунта и материалов, можно принять плотность, прочность, размеры тел –

В дальнейшем в процессе эксперимента число измерений не должно быть меньше .

Оценки измерений с помощью величины и по приведенным методам справедливы при больших > 30.

Для нахождения границ доверительного интервала при малых значениях применяют метод, предложенный в 1908 г английским математиком В.С. Госсетом (псевдоним Стьюдент).

Уравнение распределения Стьюдента имеет вид

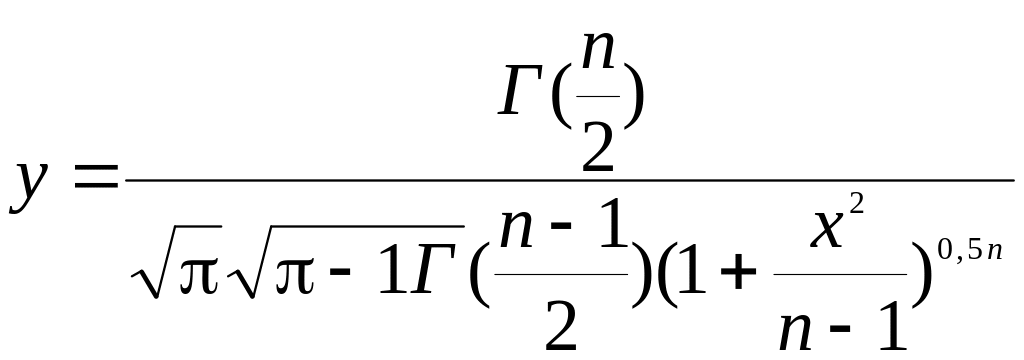, (125)

где – гамма-функция.

Как видно из рис. 28 кривые распределения Стьюдента при (практически при > 20) переходят в кривые нормального распределения.

Д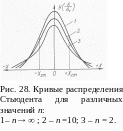 ля малой выборки доверительный интервал

, (126)

здесь – коэффициент Стьюдента, принимаемый по таблице в зависимости от значения доверительной вероятности .

Зная можно вычислить действительное значение изучаемой величины для малой выборки:

. (127)

Возможна иная постановка задачи. По известных измерений малой выборки необходимо определить доверительную вероятность при условии, что погрешность среднего значения не выйдет за пределы .

Задачу решают в такой последовательности. Вычисляют среднее значение и . По величине , известному и таблице определяют доверительную вероятность.

Оценка результатов измерений, содержащих грубые ошибки.

Появление этих ошибок вполне вероятно, а наличие их ощутимо влияет на результат измерений. Так, уже одна грубая ошибка в 25 измерениях значительно искажает экспериментальные данные. При анализе эксперимента необходимо, прежде всего, исключить грубые ошибки. Однако прежде чем исключить то или иное измерение, необходимо убедиться, что это действительно грубая ошибка, а не отклонение вследствие статистического разброса.

Известно несколько методов определения грубых ошибок статистического ряда. Пусть имеется статистический ряд малой выборки, подчиняющийся закону нормального распределения. При наличии грубых ошибок критерии их появления

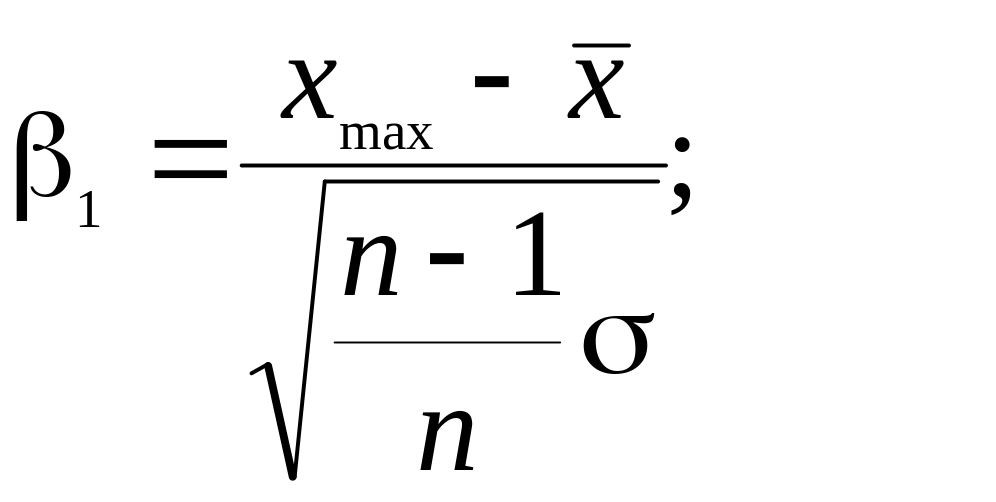
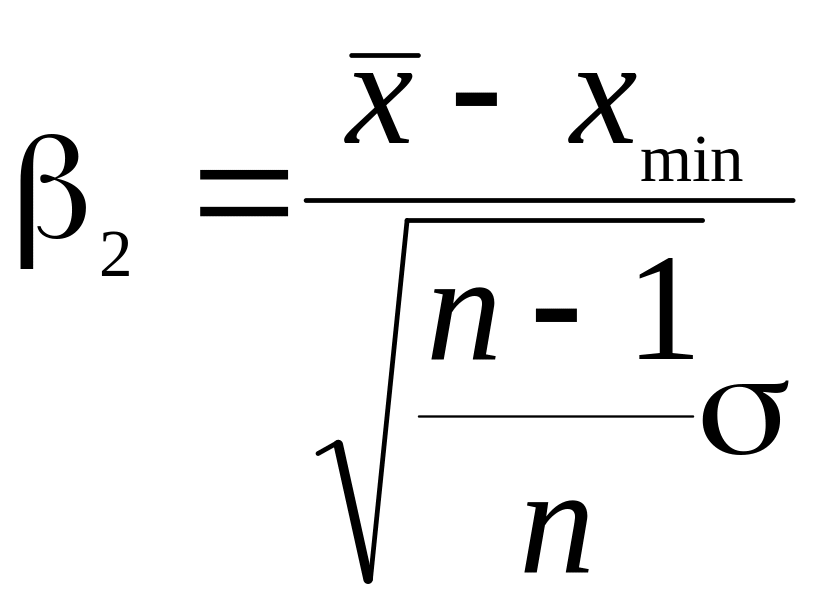, (128)

где , – наибольшее и наименьшее значение из измерений.

Составляют таблицу, в которой приводятся в зависимости от доверительной вероятности максимальные значения , возникающие вследствие статистического разброса. Если > , то значение необходимо исключить из статистического ряда как грубую погрешность. При < исключается величина . После исключения значений грубых ошибок определяют новые значения и из или измерений.

При анализе измерений можно применять для приближенной оценки следующую методику:

вычисляют по (118) среднеквадратичное отклонение ;

определяют по (122) ;

принимают доверительную вероятность и находят доверительные интервалы по (126);

окончательно устанавливают действительное значение измеряемой величины по формуле (127).

Приведенная методика целесообразна лишь для второстепенных экспериментов.

При более глубоком анализе экспериментальных данных рекомендуется следующая методика.

1. После получения экспериментальных данных в виде статистического ряда его анализируют. Проведя повторные измерения в одних и тех же условиях, предварительно исключают систематические ошибки (см. выше).

2. Анализируют ряд в целях обнаружения грубых ошибок и промахов:

устанавливают подозрительные значения или ;

определяют среднеквадратичное отклонение ;

вычисляют по (128) критерии и сопоставляют с или ;

исключают при необходимости из статистического ряда или и получают новый очищенный статистический ряд из новых членов.

3. Вычисляют среднеарифметическое , погрешности отдельных измерений и среднеквадратичное отклонение очищенного ряда .

4. Находят среднеквадратичное отклонение серии измерений, коэффициент вариации .

5. При большой выборке задаются доверительной вероятностью или уравнением значимости и по таблице определяют . При малой выборке в зависимости от принятой доверительной и числа членов ряда принимают коэффициент Стьюдента ; по формуле (126) для большой выборки или для малой выборки определяют доверительный интервал.

6. Устанавливают по (127) действительное значение исследуемой величины.

7. Оценивают относительную погрешность результатов серии измерений при заданной доверительной вероятности или

, % (129)

Если величина погрешности серии измерений соизмерима с величиной погрешности прибора , то границы доверительного интервала можно вычислить так:

. (130)

Формулой (129) следует пользоваться при , если же >3 , то доверительный интервал вычисляют с помощью (118 или 126).

Пример. Имеется 18 измерений (табл. 11). Необходимо их проанализировать. Анализ средств и результатов показал, что систематических ошибок в эксперименте не обнаружено.

Выясним, не содержат ли измерения грубых ошибок. Воспользуемся первым методом (критерий ). Вычислим среднеарифметическое и средне-

квадратичное отклонение .

Таблица 11

№ п/п
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18	67 67 68 68 69 70 71 73 74 75 76 77 78 79 80 81 82 92	– 8 – 8 – 7 – 7 – 6 – 5 – 4 – 2 – 1 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 17	– 7,83 – 7,83 – 6,83 – 6,83 – 5,83 – 4,83 – 3,83 – 1,83 – 0,83 + 0,17 + 1,17 + 2,17 + 3,17 + 4,17 + 5,17 + 6,17 + 7,17 + 17,17	64 64 49 49 36 25 16 4 1 0 1 4 9 16 25 36 49 289
			Проверка – 46,5 + 46,5

При вычислении удобно пользоваться следующей формулой:

,

где – среднее произвольное число.

Для вычисления примем произвольно .

Тогда .

В формуле (118) величину можно вычислить упрощенным методом:

.

В данном случае .

По таблице , коэффициент вариации .

Вычисляем

.

Как видно из таблицы при доверительной вероятности

и . Поскольку < , то измерение 92 не является грубым промахом.

Воспользуемся вторым методом. Для п = 18 по таблице q = 2,17 при доверительной вероятности 0,95 и = 3,00 , если = 0,99.

Предельно допустимая абсолютная ошибка отдельного измерения

при = 0,95 = 6,58 · 2,17 = 14,3 ;

при = 0,99 = 6,58 · 3,00 = 19,7 .

Следовательно, при доверительной вероятности 0,95(92 – 74,8) > 14,3 и

измерение 92 необходимо из ряда исключить. Если же доверительную вероятность принять равной 0,99 , то (92 – 74,8) < 19,7 и измерение 92 следует оставить.

В случае, когда измерение 92 исключается, то = 73,8; = 5,15.

Вычисляем среднеквадратичное отклонение для всей серии измерений:

при =18 ;

при очищенном ряде =17 .

Таким образом, при очищенном ряде точность измерений повышается на 27 %.

Определим границы доверительного интервала. Поскольку < 20, то ряд следует отнести к малой выборке. Поэтому доверительный интервал вычислим с применением коэффициента Стьюдента . По таблице принимаем доверительную вероятность 0,95 и = 2,11 при = 18; =2,12 при =17. Вычисляем доверительный интервал:

при = 18 1,55 · 2,11 = 3,2;

при = 17 1,25 · 2,18 = 2,7.

Вычислим действительное значение изучаемой величины

при = 18 = 74,8 3,2;

при = 17 = 73,8 ± 2,7.

Оценим относительную погрешность результатов серий измерений:

при = 18

при = 17

Таким образом, если принять за грубый промах, погрешность измерения уменьшается на 14 %. Если необходимо определить минимальное количество измерений при заданной точности измерений, проводят серию опытов, вычисляют , затем по формуле (123) определяют .

В данном случае Допустим, задана точность и при доверительной вероятности Имеем

при измерений;

при измерений.

Таким образом, повышение точности измерения значительно увеличивает повторность опытов.

Во многих случаях в процессе экспериментальных исследований приходится иметь дело с косвенными измерениями. При этом неизбежно в расчетах применяют те или иные функциональные зависимости типа

. (131)

Поскольку в данную функцию подставляют не истинные, а приближенные значения, то и окончательный результат также будет приближенным. В связи с этим одной из основных задач теории случайных ошибок является определение ошибки функции, если известны ошибки их аргументов.

При исследовании функции одного переменного предельные абсолютные и относительные ошибки (погрешности) вычисляют по формулам

; (132)

, (133)

где – производная функция ;

– дифференциал натурального логарифма функции.

Если исследуется функция многих переменных, то

, (134)

. (135)

В уравнениях (134) и (135) под знаком суммы и дифференциала принимают абсолютные величины. Методика определения ошибок с помощью этих уравнений следующая.

1. Определяют абсолютные и относительные ошибки аргументов (независимых переменных). Обычно величина каждого переменного измерена, следовательно, абсолютные ошибки для аргументов известны, т.е. . Вычисляют относительные ошибки независимых переменных:

(136)

2. Находят частные дифференциалы функции и по формуле (134) вычисляют в размерностях функции .

3. С помощью (135) вычисляют .

Одной из задач теории измерений является установление оптимальных, т.е. наиболее выгодных, условий измерений. Оптимальные условия измерений в данном эксперименте имеют место при . Методика решения этой задачи сводится к следующему. Если исследуют функцию с одним неизвестным переменным, то вначале берут первую производную по . Приравняв ее к нулю, определяют . Если вторая производная по будет положительной, то функция (131) при имеет минимум. При наличии нескольких переменных поступают аналогичным образом, но берут производные по всем переменным . В результате минимизации функций устанавливают оптимальную область измерений (интервал температур, напряжений, силы тока, угла поворота стрелки на приборе и т.д.) каждой функции , при которой относительная ошибка измерений минимальна; .

В исследованиях часто возникает вопрос о достоверности данных, полученных в опытах. Проиллюстрируем это примером. В исследованиях влияние вибрационного перемешивания на прочность бетона установлено: прочность контрольных образцов Па, прочность бетонных образцов после виброперемешивания Па.

Прирост прочности составляет 15%. Это упрочнение относительно небольшое, его можно отнести за счет разброса опытных данных. В этом случае проводят проверку на достоверность экспериментальных данных по условию

(137)

В данном случае проверяется разница Па, ошибка измерения равна , поэтому

(138)

Следовательно, полученный прирост прочности является достоверным.

В настоящее время имеется программа для ПЭВМ «Статистика», позволяющая определить погрешность измерений, достоверность данных эксперимента, получить аппроксимирующие уравнения, а также определить погрешность данных опытов и результатов теоретических исследований.