
- •Введение
- •1. Наука и научное исследование
- •1.1 Наука
- •1.2 Научное исследование
- •1.3 Научно-техническая информация
- •2 Выбор и формулирование темы научного
- •3. Формулирование цели и задач исследования
- •4. Методы теоретических исследований
- •4.1 Методология теоретических исследований
- •4.2 Аналитические методы исследований
- •5 Вероятностно-статистические методы
- •6. Методы системного анализа
- •Методы экспериментальных исследований
- •1 Методология экспериментальных исследований
- •2 Планирование и стратегия эксперимента
- •3. Планирование многофакторных экспериментов
- •4. Статистический анализ уравнений регрессии
- •5. Методы графического изображения результатов измерений
- •6. Методы подбора эмпирических формул
- •7. Корреляционный анализ
- •8. Анализ теоретико-экспериментальных исследований
- •9. Методы оценки измерений
- •10. Средства измерений
- •Общие требования и правила оформления научных исследований и их эффективность
- •1. Общие требования к научно-исследовательской работе
- •2. Правила оформления научно-исследовательской работы
- •3. Рецензирование научно-исследовательских работ. Доклад о работе. Составление тезисов доклада
- •4. Подготовка научных материалов к опубликованию в печати
- •5. Внедрение и эффективность научных исследований
- •Список использованных источников
- •Авторский коллектив
4. Статистический анализ уравнений регрессии
Статистический анализ уравнения типа (77) осуществляется в следующей последовательности
1. Определяется дисперсия единичного измерения или дисперсия воспроизводимости
 ,
(83)
,
(83)
где
![]() –
число повторных опытов в точках плана.
–
число повторных опытов в точках плана.
2. Определяется дисперсия среднего значения выхода
 (84)
(84)
3. Проверка однородности дисперсии при
помощи различных статистических
критериев. Если число повторных опытов
во всех точках плана одинаковое, то
можно использовать критерий Кохрена –
![]() ,
согласно которому при наличии дисперсии
по строчкам (81) и их суммы
,
согласно которому при наличии дисперсии
по строчкам (81) и их суммы
![]()
для проверки равноточности измерений
необходимо выбрать максимальную
дисперсию из ряда построчных
![]() и найти расчетное значение
и найти расчетное значение
 (85)
(85)
Гипотеза об однородности дисперсий
принимается, если расчетное значение
![]() не превышает табличного.
не превышает табличного.
4. Определяем ошибку эксперимента
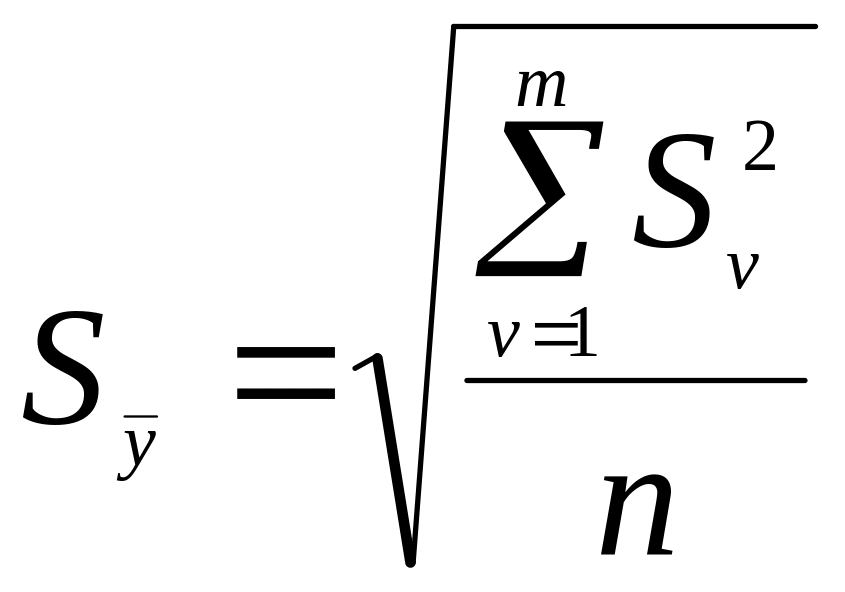 (86)
(86)
5. Значимость каждого коэффициента модели проводится независимо с помощью критерия Стьюдента ( – критерий). Для этого находим дисперсию коэффициента регрессии
![]() (87)
(87)
с
![]() степенями
свободы, а затем рассчитываем значения
критерия
степенями
свободы, а затем рассчитываем значения
критерия
![]() (88)
(88)
Если
![]() >
>![]() (табличное
значение), то
(табличное
значение), то
![]() считается значимым
считается значимым
6. Строим доверительный интервал длиной
![]() ,
где
,
где
![]()
Коэффициент значим, если его абсолютная величина больше половины длины доверительного интервала.
Проверку адекватности результатов исследования можно провести по критерию Фишера
![]() ,
(89)
,
(89)
где при равном числе дублирующих ответов
![]() ,
(90)
,
(90)
где
![]() –
число членов аппроксимирующего полинома
(включая свободный член);
–
число членов аппроксимирующего полинома
(включая свободный член);
![]() –
значение выходной величины, полученное
из уравнения регрессии.
–
значение выходной величины, полученное
из уравнения регрессии.
Дисперсия адекватности определяется с числом степеней свободы:
![]()
Во всех случаях,
когда
![]() <
<![]() ,
аппроксимация адекватна. Результаты
статистического анализа и проверки
основных критериев сводятся в типовые
таблицы.
,
аппроксимация адекватна. Результаты
статистического анализа и проверки
основных критериев сводятся в типовые
таблицы.
5. Методы графического изображения результатов измерений
При обработке результатов измерений и наблюдений широко используют методы графического изображения.
Результаты измерений, представленные в табличной форме, не позволяют достаточно наглядно характеризовать закономерности изучаемых процессов. Графическое изображение дает наиболее наглядное представление о результатах экспериментов, позволяет лучше понять физическую сущность исследуемого процесса, выявить общий характер функциональной зависимости изучаемых переменных величин, установить наличие максимума или минимума функции.
После обработки результатов измерений и оценки степени точности необходимо их свести в таблицы для анализа. Данные таких таблиц обрабатывают графическими методами.
Для графического изображения результатов измерений (наблюдений), как
п равило,
применяют систему прямоугольных
координат. Если анализируется графическим
методом функция
,
то наносят в системе прямоугольных
координат значения
равило,
применяют систему прямоугольных
координат. Если анализируется графическим
методом функция
,
то наносят в системе прямоугольных
координат значения
![]() (рис.18).
(рис.18).
Прежде чем строить график, необходимо знать ход (течение) исследуемого явления.
Как правило, качественные закономерности и форма графика экспериментатору ориентировочно известны из теоретических исследований.
Точки на графике необходимо соединять плавной линией так, чтобы она по возможности ближе проходила ко всем экспериментальным точкам. Если соединить точки прямыми отрезками, то получим ломаную кривую. Она характеризует изменение функции по данным эксперимента. Обычно функции имеют плавный характер. Поэтому при графическом изображении результатов измерений следует проводить между точками плавные кривые. Резкое искривление графика объясняется погрешностями измерений. Если бы эксперимент повторили с применением средств измерений более высокой точности, то получили бы меньшие погрешности, а ломаная кривая больше бы соответствовала плавной кривой.
О днако
могут быть исключения. Так, иногда
исследуются явления, для которых в
определенных интервалах наблюдается
быстрое скачкообразное изменение одной
из координат (рис. 19). Это объясняется
сущностью физико-химических процессов,
например, фазовыми превращениями влаги
при исследовании промерзающих систем,
радиоактивным распадом атомов в процессе
исследования радиоактивности и т.д.
днако
могут быть исключения. Так, иногда
исследуются явления, для которых в
определенных интервалах наблюдается
быстрое скачкообразное изменение одной
из координат (рис. 19). Это объясняется
сущностью физико-химических процессов,
например, фазовыми превращениями влаги
при исследовании промерзающих систем,
радиоактивным распадом атомов в процессе
исследования радиоактивности и т.д.
В таких случаях необходимо наиболее тщательно соединять точки кривой. Общее «осреднение» всех точек плавной кривой может привести к тому, что скачок функции подменяется погрешностями измерений.
Иногда при построении графика одна – две точки резко удаляются от кривой. Вначале нужно проанализировать физическую сущность явления, и если нет основания полагать наличия скачка функции, то такое резкое отклонение можно объяснить грубой ошибкой или промахом. Это может возникнуть тогда, когда данные измерений предварительно не исследовались на наличие грубых ошибок измерений. В таких случаях необходимо повторить измерение в диапазоне резкого отклонения точки. Если прежнее измерение оказалось ошибочным, то на график наносят новую точку. Если же повторные измерения дадут прежние значения, необходимо к этому интервалу кривой отнестись очень внимательно и особо тщательно проанализировать физическую сущность явления.
Часто при графическом изображении
результатов экспериментов приходится
иметь дело с тремя переменными
![]()
В этом случае применяют метод разделения
переменных. Одной из величин
![]() в пределах интервала измерений
в пределах интервала измерений
![]() задают несколько последовательных
значений. Для двух остальных переменных
и
(при
задают несколько последовательных
значений. Для двух остальных переменных
и
(при
![]() )
строят графики
)
строят графики
![]() .
В результате на одном графике получают
семейство кривых
для различных значений
(см. рис.20).
.
В результате на одном графике получают
семейство кривых
для различных значений
(см. рис.20).
Е сли
необходимо графически изобразить
функцию с четырьмя и более переменными
сли
необходимо графически изобразить
функцию с четырьмя и более переменными
![]() ,
то строят серию графиков типа предыдущих
(см. рис. 20), но каждый из них при
,
то строят серию графиков типа предыдущих
(см. рис. 20), но каждый из них при
![]() или принимают из
переменных
или принимают из
переменных
![]() постоянными и строят графики: вначале
постоянными и строят графики: вначале
![]() ,
далее
,
далее
![]() ,
,
![]() и т.д. Таким образом, можно проследить
изменение любой переменной величины
функции от других при постоянных
значениях остальных.
и т.д. Таким образом, можно проследить
изменение любой переменной величины
функции от других при постоянных
значениях остальных.
Этот метод графического анализа требует тщательности, большого внимания к результатам измерений. Однако он в большинстве случаев является простым и наглядным.
При графическом изображении результатов экспериментов большую роль играет выбор системы координат или координатной сетки. Координатные сетки бывают равномерными и неравномерными. У равномерных координатных сеток ординаты и абсциссы имеют равномерную шкалу. Например, в системе прямоугольных координат длина откладываемых единичных отрезков на обеих осях одинаковая.
Из неравномерных координатных сеток наиболее распространены полулогарифмические, логарифмические, вероятностные.
Полулогарифмическая сетка имеет равномерную ординату и логарифмическую абсциссу (рис.21).
Логарифмическая координатная сетка имеет обе оси логарифмические (см. рис. 21), вероятностная – ординату, обычно равномерную, и абсциссу – вероятностную шкалу (рис.22).
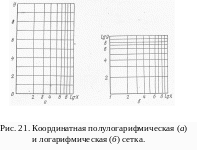
Рис.5. Координатная
вероятностная
сетка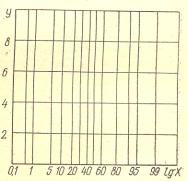
Рис. 22. Координатная
вероятностная
сетка
Назначение неравномерных сеток различное. В большинстве случаев их применяют для более наглядного изображения функций. Функция имеет различную форму на различных сетках. Так, многие криволинейные функции спрямляют на логарифмических сетках.
Большое значение в практике графического изображения экспериментальных данных имеет вероятностная сетка, применяемая в различных случаях: при обработке измерений для оценки их точности, при определении расчетных характеристик (расчетной влажности, расчетных значений модуля упругости грунта и горных пород, межремонтных сроков службы одежды и покрытий и т. д.).
Иногда в процессе обработки экспериментальных данных графическим способом необходимо составить расчетные графики, ускоряющие нахождение по одной переменной других, при этом существенно повышаются требования к точности вычерчивания функции на графике.
Вычерчивая расчетные графики, необходимо руководствоваться следующими практическими рекомендациями. В зависимости от числа переменных нужно выбрать координатную сетку и определить вид графика – одна кривая, семейство кривых или серия семейств. Большое значение приобретает выбор масштаба графика, что связано с размерами чертежа и соответственно с точностью снимаемых с него значений величин. Известно, что чем крупнее масштаб, тем выше точность снимаемых значений. Однако, как правило, графики не превышают размеров 20×15 см, что является удобным при составлении отчетов. Лишь в отдельных случаях используют графики больших размеров.
О пыт
показывает, что применяемая для
вычерчивания графиков миллиметровая
бумага в пределах размеров 15 – 20 см дает
погрешность ± 0,1–0,2 мм. Это следует иметь
в виду при вычерчивании расчетных
графиков. Таким образом, абсолютная
ошибка снимаемых с графиков величин
может достигать
пыт
показывает, что применяемая для
вычерчивания графиков миллиметровая
бумага в пределах размеров 15 – 20 см дает
погрешность ± 0,1–0,2 мм. Это следует иметь
в виду при вычерчивании расчетных
графиков. Таким образом, абсолютная
ошибка снимаемых с графиков величин
может достигать
![]() ,
где
,
где
![]() –
принятый масштаб графика. Очевидно, что
точность измерений может быть выше
точности снимаемых с графика величин.
–
принятый масштаб графика. Очевидно, что
точность измерений может быть выше
точности снимаемых с графика величин.
Масштаб по координатным осям обычно применяют различный. От выбора его зависит форма графика – он может быть плоским (узким) или вытянутым (широким) вдоль оси (рис.23).
Узкие графики дают большую погрешность по оси , широкие – по оси .
Из рисунка видно, что правильно подобранный масштаб (нормальный график) позволяет существенно повысить точность отсчетов.
Расчетные графики, имеющие максимум (минимум) функции или какой-либо сложный вид, особо тщательно необходимо вычерчивать в зонах изгиба. На таких участках количество точек для вычерчивания графика должно быть значительно больше, чем на плавных участках.
В некоторых случаях строят номограммы, существенно облегчающие применение для систематических расчетов сложных теоретических или эмпирических формул в определенных пределах измерения величин. Номограммированы могут быть любые алгебраические выражения. В результате сложные математические выражения можно решать сравнительно просто графическими методами. Построение номограмм – трудоемкая операция. Однако, будучи раз построенной, номограмма может быть использована для нахождения любого из переменных, входящих в номограммированное уравнение. Применение ЭВМ существенно снижает трудоемкость номограммирования.
Существует несколько методов построения номограмм. Для этого применяют равномерные или неравномерные координатные сетки. В системе прямоугольных координат функции в большинстве случаев на номограммах имеют криволинейную форму. Это увеличивает трудоемкость, поскольку требуется большое количество точек для нанесения одной кривой.
В полу- или логарифмических координатных сетках функции имеют прямолинейную форму и составление номограмм упрощается.
Методика построения номограмм функции
одной переменной
или многих
![]() описана ранее и сводится к построению
кривой, семейства или серии семейств
путем принятия постоянных и нахождения
одной переменной.
описана ранее и сводится к построению
кривой, семейства или серии семейств
путем принятия постоянных и нахождения
одной переменной.
Сложные алгебраические выражения
целесообразно сводить к простому
произведению двух-трех значений,
например:
![]() ,
где
–
функции
,
где
–
функции
двух, трех переменных.
В этом случае необходимо вначале, задавшись переменными, вычислить , далее, придавая им постоянные значения, найти . Величины необходимо варьировать в определенных значениях, например, от 0 до 100 через 5 или 10.
Наиболее эффективным является такой способ построения номограмм, при котором представляются как безразмерные критерии.
