
- •Підготовка
- •1. Обчислення
- •2. Тотожні перетворення
- •3. Рівняння. Системи рівнянь
- •4. Нерівності. Системи нерівностей
- •5. Функції
- •6. Послідовності. Елементи прикладної математики
- •7. Задачі
- •8 . Кути. Трикутники
- •9. Многокутники
- •10. Коло
- •11. Декартові координати та вектори на площині
- •Бланк відповідей для першої та другої частини атестаційної роботи
4. Нерівності. Системи нерівностей
Доведення нерівностей. Способи розв’язування нерівностей. Системи нерівностей. («Алгебра», с. 10 – 12).
1(1). Яке з чисел є розв’язком нерівності х2 – 2х < 0?
А) –1 Б) 0 В) 1 Г) 2
2(2).
Розв’яжіть
нерівність
![]()
3(1). Скільки цілих розв’язків має нерівність 2х2 – х + 1 ≤ 0?
4(2). Знайдіть найменше ціле число, що є розв’язком нерівності 12 + 4х – х2 > 0.
5(1). На
якому з рисунків зображено множину
розв’язків системи нерівностей
![]()
А)![]() Б)
Б)![]() В)
В)![]() Г)
Г)![]()
6(3).
Знайдіть
цілі числа, що є розв’язками системи
нерівностей
![]()
7(3). Доведіть, що 10a2 – 6a – 2ab + b2 + 2 > 0 для усіх дійсних чисел a та b.
Завдання для самостійної роботи
8(1). Розв’яжіть нерівність 6х < 16 – 2х.
9(1). Знайдіть кількість цілих розв’язків нерівності – 12 < 8х – 4 ≤ 12.
10(1). Розв’яжіть нерівність 9х2 – 6х + 1 > 0.
А)
(–∞; ∞) Б)
![]() В)
В)
![]() Г)
Г)
![]()
11(2). Знайдіть найменше ціле число, що є розв’язком нерівності
(х – 3)(х + 3) – 4х ≤ (х – 1)2 – 5.
12(2). Розв’яжіть нерівність (3х + 2)2 + (4х – 3)2 ≤ (5х – 1)2.
13(1). Яка з наведених систем нерівностей не має розв’язків?
А)![]() Б)
Б)![]() В)
В)![]() Г)
Г)![]()
14(3).
Розв’яжіть
систему нерівностей
![]()
15(3). Доведіть, що для всіх дійсних значень а виконується нерівність
(а – 2)2 – 5 > 2(а – 6).
Відповіді. 8. (–∞; 2) 9. 3 10. В 11. –2 12. [6; ∞) 13. Б 14. {–3}U[2; ∞) 15. (a – 3)2 + 2 > 0
5. Функції
Види функцій та їх графіки. Властивості функцій. Побудова та перетворення графіків.(«Алгебра», с. 14 – 16).
1(1).
Знайдіть значення функції
![]() ,
якщо значення аргументу дорівнює –2.
,
якщо значення аргументу дорівнює –2.
2(1). Для якої з функцій областю визначення є множина (–∞; 2)?
А)
![]() Б)
Б)
![]() В)
В)
![]() Г)
Г)
![]()
3(1). Графіком якої з функцій є пряма, що проходить через початок координат?
А) у = х2 Б) у = 2х В) у = 2х – 7 Г) у = 2
4(1). Яка з наведених функцій не є оберненою пропорційністю?
А)
![]() Б)
Б)
![]() В)
В)
![]() Г)
Г)
![]()
5(1). Яка з наведених функцій спадає на інтервалі (0; +∞)?
А)
![]() Б)
Б)
![]() В)
В)
![]() Г)
Г)
![]()
6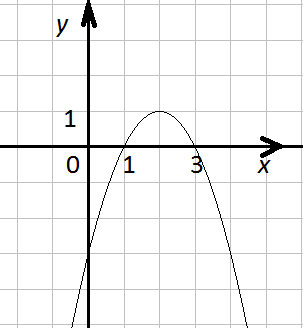 (1).
Знайдіть
область значень функції у
= х2
– 5.
(1).
Знайдіть
область значень функції у
= х2
– 5.
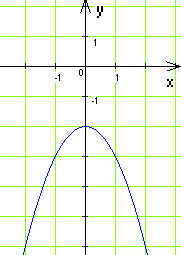
7(1). На рисунку зображено графік функції
у = – х2 + 4х – 3. Розв’яжіть нерівність
– х2 + 4х – 3 ≤ 0.
8(2).
Знайдіть
інтервал зростання функції
![]()
9(3). Парабола у = ах2 + bх + с має вершину в точці А(1; 5) та перетинає вісь ординат в точці В(0; 7). Знайдіть значення коефіцієнтів а, b, с.
10(2). Знайдіть координати точок параболи у = х2 + х – 3, у яких абсциса на 2 більша за ординату.
11(3).
Побудуйте графік функції
![]()
Завдання для самостійної роботи
12(1). Через яку з даних точок проходить графік рівняння 5у – 3х = –1?
А) (2; –1) Б) (–2; 1) В) (2; 1) Г) (–2; –1)
13(3).
Знайдіть
область визначення функції
![]()
14(1). Графік якої з функцій проходить через початок координат?
А)
у
= 0,1х
+ 10 Б) у
= –5х
+ 0,5 В)
![]() Г) у
= 0,8х
– 40
Г) у
= 0,8х
– 40
15(1).
На
якому з рисунків зображено графік
функції
![]()
А)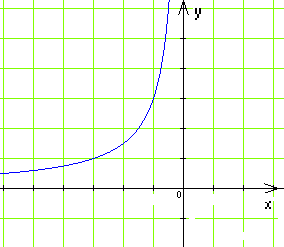 Б)
Б)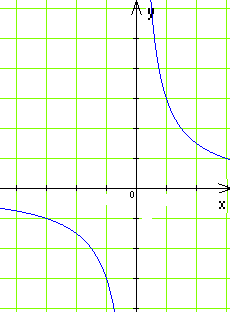 В)
В)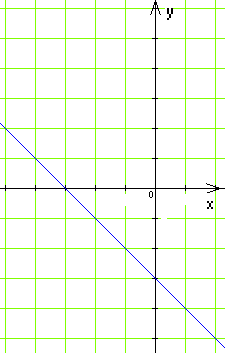 Г)
Г)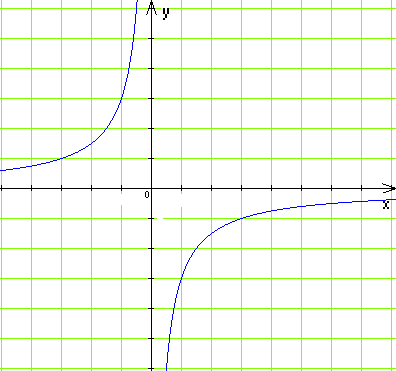
16(1). На якому з рисунків зображено графік функції у = 2?
А)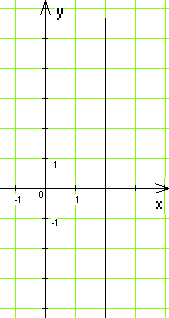 Б)
Б)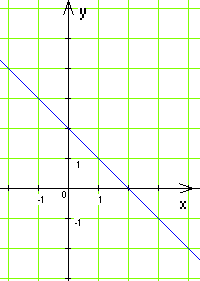 В)
В)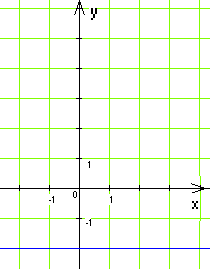 Г)
Г)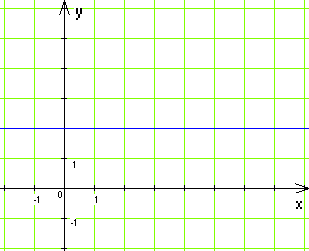
17(2).
Побудуйте графік функції
![]() .
При яких значеннях
х
виконується нерівність
.
При яких значеннях
х
виконується нерівність
![]()
18(1). На якому з рисунків зображено графік функції у = – х2 – 2?
А)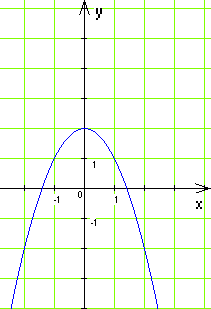 Б)
Б)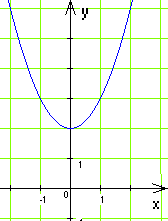 В)
В)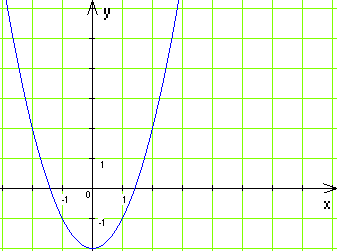 Г)
Г)
19(2). Знайдіть область значень функції у = – х2 + 2х + 7.
20(2).
Знайдіть
інтервал спадання функції
![]()
21(2). При яких значеннях а та с графік функції у = ах2 – 2х + с проходить через точки А(1; 6) та В(2; 19)?
22(2). Знайдіть координати точок параболи у = х2 – 2х + 4, у яких сума абсциси та ординати дорівнює 4.
2 3(3).
Побудуйте графік функції
3(3).
Побудуйте графік функції
![]() .
.
Відповіді. 12. В 13. (–∞; –3)U(–3; 2]U[5; +∞) 14. В 15. Г 16. Г 17. [0; 9) 18. Г 19. (–∞; 8] 20. [3; +∞) 21. a = 5, c = 3
22. (0; 4), (1; 3) 23. Графік зображено на рисунку
