Глава IV. Многочлены
§ 9. Сумма и разность многочленов
25. Многочлен и его стандартный вид
Выражение
представляет
собой сумму одночленов
Такие выражения называют многочленами.
Определение. Многочленом называется сумма одночленов.
Одночлены из которых составлен многочлен, называют членами многочлена.
Если многочлен состоит из двух членов, его называют двучленом; если из трех членов – трехчленом. Одночлен считают многочленом, состоящим из одного члена.
В
многочлене
члены
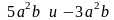являются подобными слагаемыми, так как
они имеют одну и ту же буквенную часть.
Подобными слагаемыми являются и члены
не
имеющие буквенной части. Подобные
слагаемые в многочлене называют подобными
членами многочлена,
а приведение подобных слагаемых в
многочлене – приведением
подобных членов многочлена.
Пример 1. Приведем подобные члены в многочлене
► Имеем
Каждый
член многочлена
является
одночленом стандартного вида, и этот
многочлен не содержит подобных членов.
Такие многочлены называют многочленами
стандартного вида.
Любой многочлен можно привести к стандартному виду. Для этого нужно каждый его член представить в стандартном виде и привести подобные члены.
Членами
многочлена стандартного вида
служат одночлены второй, пятой и нулевой
степеней. Наибольшую из этих степеней
называют степенью многочлена. Таким
образом, многочлен
является
многочленом пятой степени.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
Пример 2. Выясним, какова степень многочлена
►Для этого приведем его к стандартному виду:
Степень
многочлена
равна
двум, поэтому степень многочлена
также равна двум.
26. Сложение и вычитание многочленов
Сложим
многочлены
Для этого составим их сумму, затем раскроем скобки и приведем в полученном многочлене подобные члены:
Вычтем
из многочлена
многочлен
Для этого составим их разность, затем раскроем скобки и приведем в полученном многочлене подобные члены:
Иногда
требуется решить обратную задачу –
представить многочлен в виде суммы или
разности многочленов. При этом пользуются
правилом: если
перед скобками ставится знак «плюс»,
то члены, которые заключают в скобки,
записывают с теми же знаками; если перед
скобками ставится знак «минус», то знаки
членов, заключаются в скобки, меняют на
противоположные.
Например:
27. Умножение одночлена на многочлен
Умножим
одночлен
на многочлен
Правило умножения одночлена на многочлен: чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Задача.
Разъясните геометрический смысл формулы
28. Вынесение общего множителя за скобки
Представление многочлена в виде произведения двух или нескольких многочленов называют разложением многочлена на множители.
Пример.
Разложить на множители многочлен
Примененный способ разложения многочлена на множители называют вынесением общего множителя за скобки.