А.Р. Ганеева линия тождественных преобразований в неполной средней школе
У математиков существует свой язык – формулы.
С. Ковалевская
ВОПРОСЫ ДЛЯ ПРЕДВАРИТЕЛЬНОГО ОБСУЖДЕНИЯ
1. Что называют математическими выражениями? Приведите примеры.
2. Где вы встречались с тождественными преобразованиями?
3. Когда и кем был введен знак «≡» для обозначения тождества?
Линия тождественных преобразований в курсе математики средней школы и ее взаимосвязь с другими линиями школьного курса.
Тождественное преобразование (ТП) в математике понимается как:
• замена одного аналитического выражения другим, тождественно ему равным, но отличным по форме;
• преобразование (отображение в себя) некоторого множества, оставляющее на месте каждый его элемент.
В курсе алгебры ТП рассматриваются в первом смысле, т. е. как замена одного аналитического выражения другим, тождественно ему равным. Знак «≡» для обозначения тождества был введен Бернхардом Риманом (немецким математиком, учеником К. Гаусса) в 1857 г.
Для мотивации изучения сложных тождественных преобразований можно применить прием М. П. Синельникова. "Учитель дает довольно сложное алгебраическое выражение, например и предлагает вычислить его значение при значениях букв, задаваемых учениками. Преподаватель сразу дает ответ, который учащиеся могут найти лишь после более или менее продолжительных вычислений. Этот прием подводит учеников к понятию «тождественные выражения», вызывает у них интерес к изучению правил, по которым можно данное сложное выражение заменить более удобным для вычислений. Значение темы «Тождественные преобразования» состоит в следующем:
• ученики должны понимать, что в алгебре все действия только обозначаются, а затем преобразуются в более простые заменой суммы, произведения тождественно равным выражением;
• тождественные преобразования – не самоцель, они используются для удобства нахождения числовых значений выражений, решения уравнений, доказательства неравенств и выявления свойств функций.
Это значит, что с тождественными преобразованиями связаны все линии курса алгебры. Поэтому ТП – одна из основных линий курса алгебры и начал анализа школьной математики.
Изучение этой линии выполняет различные функции.
Теоретический аппарат служит средством построения теории других линий, таких, как «Уравнения, неравенства и их системы», «Функция» и др. Операционный аппарат является практической базой решения математических и прикладных задач. Школьный курс математики выделяет два основных класса математических выражений: алгебраические (выражения, составленные из конечного числа букв или цифр, соединенные знаками действий, порядок действий может определяться и скобками; арифметические выражения – частный вид выражений, не включающих букв) и трансцендентные (аналитические выражения, не являющиеся алгебраическими).
Основная (базовая) теория тождественных преобразований изложена на множестве алгебраических выражений. Далее при введении трансцендентных функций расширяется область применения тождественных преобразований и, что естественно, свойства введенных функций выделяют особенности преобразований неалгебраических выражений. Уровень строгости изложения темы в школьных учебниках различен.
Основные типы преобразований и этапы их изучения
В учебнике алгебры для 7 класса под редакцией С. А. Теляковского вводится понятие «тождества» на первом этапе изложения курса. Оно определяется как равенство, верное при любых значениях входящих в него переменных. Следует отметить, что этому определению предшествует определение тождественно равных выражений. Два выражения, соответственные значения которых равны при любых значениях переменных, называются тождественно равными.
С введением дробно-рациональных выражений (8 класс) авторы возвращаются к понятию тождества и определяют тождество как равенство, верное при всех допустимых значениях входящих в него переменных.
Изучение линии тождественных преобразований предполагает выделение четырех этапов: пропедевтического (5-6 классы); первого, на котором используется нерасчлененная система преобразований (начало 7 класса); второго, в процессе которого выделяются конкретные виды преобразований (8-9 классы); третьего, который организует целостную систему преобразований (10-11 классы).
Усвоение понятия буквенного выражения осуществляется посредством выполнения учащимися разнообразных письменных и устных упражнений. Вначале выполняются простые упражнения, потом со временем усвоения программы – упражнения с более сложной конструкцией выражений: вводятся новые буквы, увеличивается их число, используются числа из новых числовых множеств, разнообразятся действия над выражениями.
Рассмотрим методику ознакомления учащихся с математической символикой и ее использование для введения некоторых понятий.
При выполнении упражнений всегда имеется в виду, что работа с буквенными данными является естественным продолжением работы с конкретными числами и числовыми выражениями. При выполнении заданий придерживаются общепринятого положения, высказанного профессором В. Л. Гончаровым еще в 1955 г.: «Все, что не сразу выходит с буквами, делайте сначала с числами. Все, что сразу выходит с буквами, сейчас же проверяйте на числах». Это связано с тем, что учащиеся на первых порах испытывают затруднения в усвоении буквенной символики: в усвоении наименования и их записи. В практике обучения поэтому изыскиваются возможности более раннего проведения с учащимися беседы об использовании в математике соответствующей символики.
Содержание этой беседы может быть таким. Вначале мотивируется использование в математике буквенной символики (как средства более яркого, точного и лаконичного представления математических суждений, средства обобщения изученных свойств чисел, способа выделения изученной закономерности, алгоритма вычислений и т. п.), потом отмечается, что в алгебре часто для этой цели используются буквы латинского алфавита.
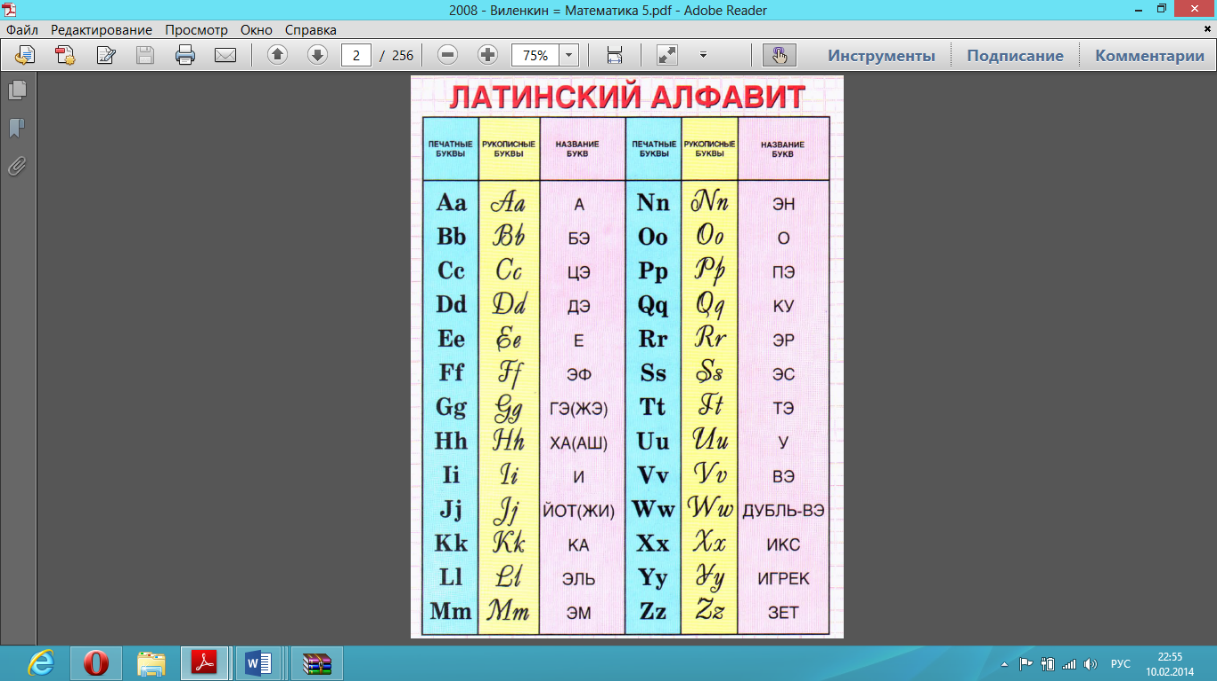
Такая таблица изготавливается для обозрения всего класса и может быть изготовлена каждым учеником в виде отдельной карточки для индивидуального пользования.
Усвоение буквенной символики осуществляется постепенно по мере раскрытия содержания курса, причем на первых порах учитель не только показывает на конкретном материале употребление букв, но и мотивирует их использование, направляет внимание учащихся на более четкое выделение с их помощью соответствующих отношений и функциональных связей, напоминает и закрепляет специфические для математики обороты речи и т. п. Важно при этом использовать задания следующих типов:
1) на чтение и понимание смысла буквенно-символической записи объектов изучения;
2) на запись объектов изучения в буквенно-символической форме;
3) на действия с объектами изучения, записанными в буквенно-символической форме.
Приведем несколько примеров заданий по каждому типу упражнений. Так, например, развитию речевых навыков содействуют такие упражнения:
1. Проанализируйте порядок выполнения действий в каждое из данных выражений и объясните, как оно читается:
Заметим, что каждому такому упражнению предшествуют аналогичные упражнения на числовом материале, например: «Прочитайте выражения: 2 + 3; 2∙3 + 4; 2∙3 + 4-5; 2∙3 – 6:2» и т. п.
Отметим,
что если алгебраическое выражение
содержит действия разных ступеней, то
при чтении его произносят сначала
последнее по порядку действие, а затем
называют остальные действия. Например,
– здесь последнее по порядку действие
– умножение, поэтому читаем так:
«Произведение разности чисел а
и b
на число с».
В учебнике по математике 5 класса Я.Н. Виленкина имеются рубрики, отмеченные славянской буквой «глаголь», которые учат говорить правильно.
Ко второму типу упражнений относятся следующие:
1. Запишите с помощью чисел, букв и знаков действий и отношений предложение:
а) произведение числа а на сумму чисел k и единицы;
б) а – отрицательное число;
в) определение модуля числа b.
2. Укажите на координатной прямой и запишите с помощью символов следующее: а) 2 – положительное число; б) – 3 – отрицательное число; в) отрицательное число, модуль которого равен 7.
3. Используя буквенную символику, запишите общий вид чисел: а) четных; б) нечетных; в) делящихся на 3; г) которые при делении на 3 дают в остатке 1.
К третьему типу упражнений относятся такие:
1.
Закончите запись:
2. В чем сходство и различие выражений
Сравните значения этих выражений при а = 2, b = 3 и с = 5.
Многие из приведенных упражнений выполняются устно. Эти упражнения часто предлагаются учащимся на этапе введения в урок в виде математического диктанта, математической разминки, устного счета и т. п/ В основном они выполняются после проверки учителем домашней работы, но перед заданиями, с помощью которых учитель вводит учащихся в новый материал. Разнотипность заданий позволяет удачно их включать в содержание учебного материала первого этапа урока.
В процессе изучения алгебраического материала данного курса используются упражнения и других типов. Основная их цель – активно использовать буквенную символику в качестве средства обобщения изученного материала. Приведем несколько примеров.
Записи законов арифметических действий в буквенной форме появляются как закономерный итог выполнения учащимися большого количества заданий с конкретными числовыми данными.
Буквенная запись свойств сложения и вычитания
Известные вам свойства сложения и вычитания можно записать с помощью букв.
1. Переместительное свойство сложения записывают так:
В этом равенстве буквы а и b могут принимать любые натуральные значения и значение 0.
2. Сочетательное свойство сложения записывают с помощь букв так:
Здесь a, b и с – любые натуральные числа или нуль.
3. Свойство нуля при сложении можно записать так:
Здесь буква а может иметь любое значение.
4. Свойство вычитания суммы из числа записывают с помощью букв следующим образом:
Здесь
или
5. Свойство вычитаний числа из суммы записывают с помощью букв так:
6. Свойства нуля при вычитании можно записать так:
Здесь а может принимать любые натуральные значения и значение 0.
Буквенная запись свойств умножения
1. Произведение двух чисел не изменяется при перестановке множителей.
Это свойство умножения называют переместительным. С помощью буке его записывают так:
2. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель
Это свойство умножения называют сочетательным. С помощью букв его записывают так:
Сумма
п
слагаемых,
каждое из которых равно 1, равна п.
Поэтому
верно равенство
Сумма
п
слагаемых,
каждое из которых равно нулю, равна
нулю. Поэтому верно равенство
Когда в записи, произведения нет скобок, умножение выполняют по порядку слева направо.
Тождества. Тождественные преобразования
Одна из важных идейных линий курса алгебры – линия тождественных преобразований. Поэтому обучение математике в 5-6 классах строится таким образом, чтобы учащиеся уже в этих классах приобрели навыки простейших тождественных преобразований (без употребления термина «тождественные преобразования»). Эти навыки формируются при выполнении упражнений на приведение подобных слагаемых, раскрытие скобок и заключение в скобки, вынесение множителя за скобки и т. д. Рассматриваются также простейшие преобразования числовых и буквенных выражений. На этом уровне обучения осваиваются преобразования, которые выполняются непосредственно на основе законов и свойств арифметических действий.
В 5 классе изучаются законы и свойства действий над неотрицательными числами:
и
т.д.
Приведем основные виды задач, при решении которых активно попользуются свойства и законы арифметических действий и через которые формируются навыки тождественных преобразований:
1) обоснование алгоритмов выполнения действий над числами изучаемых числовых множеств;
2) вычисление значений числового выражения наиболее рациональным способом;
3) сравнение значений числовых выражений без выполнения указанных действий;
4) упрощение буквенных выражений;
5) получение новых алгоритмов преобразований буквенных выражений;
6) доказательство равенства значений двух буквенных выражений.
Приведем несколько примеров.
1. Представьте число 153 в виде суммы разрядных слагаемых; и в виде разности двух чисел; в виде произведения двух чисел.
2. Представьте число 27 в виде произведений трех одинаковых множителей.
Эти упражнения на представление одного и того же числа в разных формах записи содействуют усвоению понятия о тождественных преобразованиях. Вначале эти представления могут быть произвольными, в дальнейшем – целенаправленными. Например, представление в виде суммы разрядных слагаемых используются для объяснения правил сложения натуральных чисел «столбиком», представление в виде суммы или разности «удобных» чисел – для выполнения быстрых вычислений различных произведений, представление в виде произведения множителей – для упрощения различных дробных выражений. Учащимся объясняется, что целесообразность тех или иных представлений зачастую обусловливается самой постановкой задачи.
3. Найдите значение выражения 928 ∙36 + 72 ∙ 36.
Для нахождения значения выражения целесообразно преобразовать его, применив распределительный закон:
928∙36 + 72∙36 =(928+ +72) ∙36= 1000∙36 = 36000.
4.
Приведите подобные слагаемые:
5. Решите уравнение 7,2 – (6,2 – х) = 2,2.
6. Сколько арифметических действий выполняется при вычислениях по формулам:
Всегда ли при вычислениях по этим двум формулам мы получим одинаковые результаты?
7.
Найдите значение выражения
если
8. При каких значениях х верно равенство:
Изучение тождеств и тождественных преобразований проводится в тесной связи с изучением рассматриваемых в данном курсе числовых множеств. Задания от класса к классу усложняются, но в основном путем постепенного переплетения линии тождественных преобразований с числовой и линией уравнений.
Самые первые задания, в которых требуется выполнить тождественные преобразования, просты и понятны учащимся. В других заданиях цепочки преобразований удлиняются. От учащихся требуется объяснить каждый шаг преобразования, выделить общее положение, подтверждающее правильность произведенного преобразования, а порой объяснить необходимость того или иного обоснования. При выполнении упражнений уделяется внимание формулировке правил, свойств, законов, лежащих в основе данного преобразования, а также их записи в буквенно-символической форме. На первых порах обязательны вопросы к учащимся: «Какие правила, свойства, законы использовались при выполнении задания?», «Как они читаются?», «Как записываются с помощью символов?» и др.
В тождественных преобразованиях алгебраических выражений используются два правила: подстановки и замены равным. В данном курсе математики широко используется операция подстановки (на ней основан счет по формулам). Здесь нередко учащиеся ошибаются. Например, при нахождении числового значения выражения ab при а = 5 и b = – 3 учащиеся полагают, что получится 5 – 3 = 2. Предупреждению ошибок содействует тщательно проводимый анализ выражений (так же как и при решении задач, анализ их условия). На первых порах допущенные ошибки обязательно исправляются с детальным объяснением сущности данного правила подстановки. В дальнейшем учителя требуют от учащихся нахождения и самостоятельного исправления допущенной ошибки (с целью воспитания и развития профессиональных умений и навыков: самопроверки и самоконтроля), и обязательно навыки правильного выполнения операции закрепляются системой соответствующих упражнений. Заметим здесь также, что само по себе выполнение большого числа разнообразных упражнений не всегда обеспечивает получение желаемого результата в обучении и развитии учащихся. Умение пользоваться законами арифметических действий помогает учащимся строить индуктивные и дедуктивные умозаключения. Такой подход помогает учащимся выработать навыки применения алгебраического аппарата и приобрести необходимую логическую культуру.