4.3. Выполнение работы

4.3.1. Описание модели

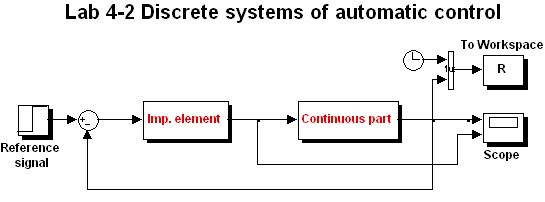
Очевидно, что при моделировании процессов в линейной импульсной системе ее S-модель должна соответствовать структурной схеме системы изображенной на рис. 4.2. Такая S-модель представлена на рис. 4.3.

Рис. 4.3. S-модель линейной импульсной системы

В состав замкнутой системы входят импульсный элемент (Imp. element) и непрерывная часть (Continuous part).

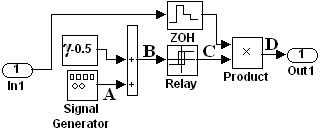
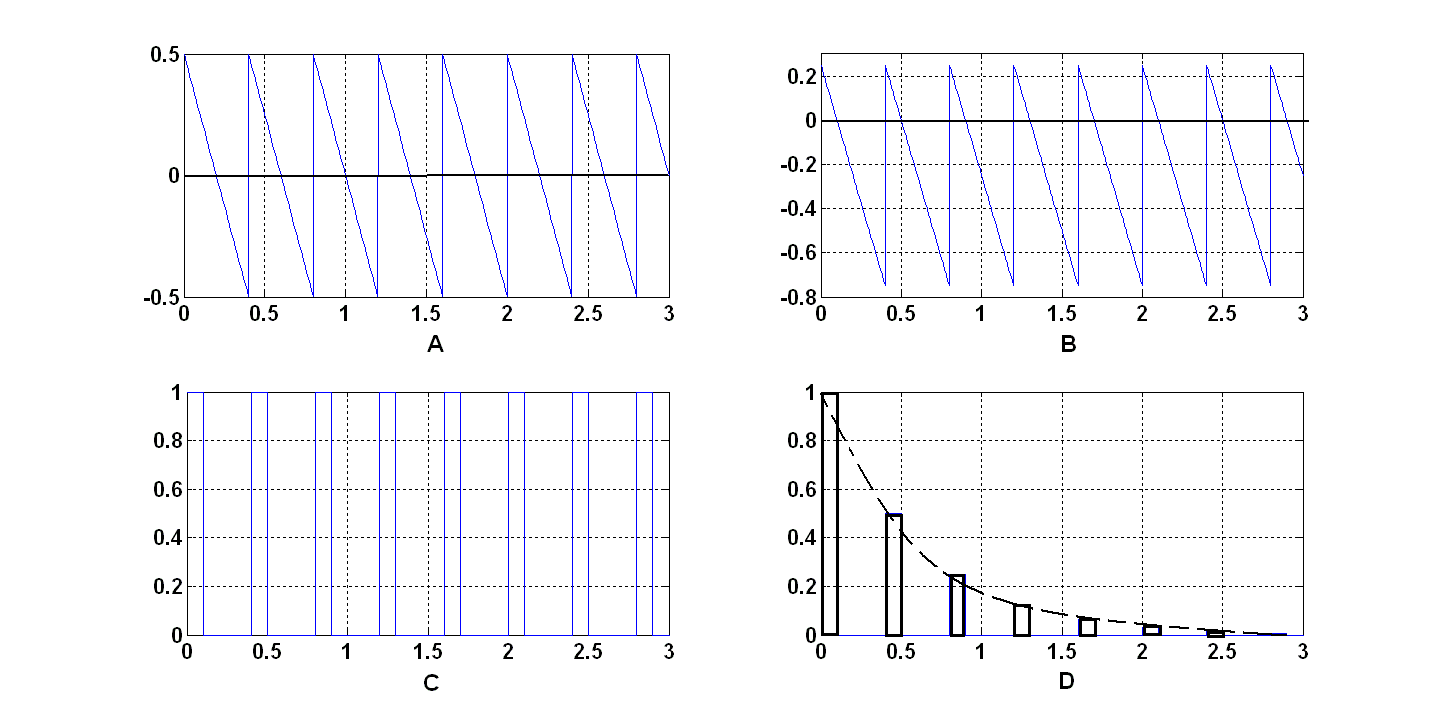
S-модель импульсного элемента, предназначенного для выработки прямоугольных импульсов с заданными значениями длительности γ и времени квантования T, представлена на рис. 4.4. Диаграммы, поясняющие работу импульсного элемента, представлены на рис. 4.5. Буквами A, B, C, D на этих рисунках обозначены зависимости генерируемого сигнала от времени для различных узлов импульсного элемента.

Основным составляющим импульсного элемента является генератор периодических сигналов, который вырабатывает пилообразный сигнал с периодом повторения и амплитудой равной 0,5 (А). Этот сигнал суммируется с постоянным сигналом величиной (γ-0,5). Это позволяет менять часть пилообразного сигнала, который расположен над осью абсцисс (В). Следующий за сумматором релейный элемент вырабатывает прямоугольные импульсы, высота которых равна единице, а длительность определяется величиной и знаком сигнала, поступающего с выхода сумматора (С). Непрерывный сигнал ошибки ε(t) преобразуется в ступенчатый сигнал в звене ZOH (Zero Order Hold – экстраполятор нулевого порядка) с тем же периодом квантования, каков период повторения пилообразного сигнала. Он, в свою очередь, после перемножения на единичные импульсы, формирует импульсы высотой равной величине сигнала ε, а длительностью γТ (D). Здесь же пунктирной линией приведен график непрерывного сигнала ошибки ε(t), являющегося входным для импульсного элемента.

Рис. 4.4. S-модель импульсного элемента

Рис. 4.5. Диаграммы, поясняющие работу импульсного элемента

Диалоговое окно блока позволяет задать параметры γ и Т.

Передаточная функция блока НЧС (Continuous part) записывается в виде:

. (4.13)

Диалоговое окно блока позволяет задать численные значения параметров, реализуя НЧС в виде идеально интегрирующего звена или в виде апериодического звена 1 порядка.

В схеме предусмотрена визуализация результатов расчета с помощью осциллографа (scope) и запись их в память (To Work space) для последующего построения графиков процессов и их анализа.

4.3.2. Настройка модели, выполнение моделирования и анализ

Выполнение работы состоит из двух частей. В первой части исследуются устойчивость импульсных систем и процессы конечной длительности в них.

Курсант, в соответствии со своим номером в академическом журнале, должен выбрать из таблицы 4.3 значения параметров передаточной функции непрерывной части системы и параметры импульсного элемента. Вначале НЧС представляется идеальным интегрирующим звеном, а потом расчеты и моделирование повторяются для апериодического звена 1 порядка. Один из параметров этих звеньев остается незаданным (в соответствующей клеточке таблицы стоит знак вопроса). Его необходимо вычислить так, чтобы замкнутая дискретная система:

• находилась на границе устойчивости;

• была настроена на процесс конечной длительности (оптимальная по быстродействию настройка).

Первый из этих пунктов требует решения алгебраического уравнения (4.11а) или (4.11б), а второй – (4.12а) или (4.12б). Уравнения (4.11а) и (4.12а) являются линейными и решаются легко, а уравнения (4.11б) и (4.12б) целесообразно решить численно, что и реализовано в предлагаемой программе расчета (М-файл сценарий) imp.m, которая приведена в приложении.

Рассмотрим это на примере. Допустим, что заданы следующие значения параметров передаточной функции непрерывной части системы – T₁=3 c (фактически задан параметр а₀), k=7,5 и значение величины заполнения импульса γ=0,8. Время квантования Т неизвестно. Процедура обращения к программе выглядит следующим образом:

>> imp

Введите значение величины постоянной времени А1 звена - T1

T1=3

Введите вектор параметров импульсной системы S, используемых для настройки на нужный режим

Первые 2 компонента вектора S, отвечают значениям двух из трех ("gamma", "T", "k") параметров, вводимых в заданной последовательности

третий компонент может принимать значения 1, 2 или 3. При этом 1 – отвечает поиску gamma", 2 – поиску "T", 3 – поиску "k".

S=[0.8 7.5 2]

Величина периода квантования при настройке на границу устойчивости T_kr=1.048

Величина периода квантования при настройке на режим кон. длительности T_opt=0.46936

Таким образом, если время квантования составляет 1,0480 с, то импульсная система находится на границе колебательной устойчивости, а если – 0,4694 с, то настроена на процесс конечной длительности (оптимальна по быстродействию).

Далее необходимо, настроив соответствующим образом каждый из блоков модели промоделировать протекание процессов в системе.

Исследуйте, как изменяются характеристики процессов (для любого из видов НЧС) при варьировании времени квантования и коэффициента усиления. Результат подтвердите графиками. Сделайте вывод.

Сравните найденные критические и оптимальные настройки для двух видов НЧС. Сделайте вывод.

Поясните отличия в характере процесса конечной длительности при включении в непрерывную часть интегрирующего и апериодического звеньев.

Во второй части работы рассчитывается переходной процесс в импульсной системе, у которой НЧС – идеальное интегрирующее звено, все значения параметров системы соответствуют найденным значениям для границы устойчивости за исключением коэффициента передачи интегрирующего звена – его величина выбирается по формуле . Далее следует:

• записать выражение для дискретной передаточной функции разомкнутой и замкнутой, используя формулы (4.6а) и (4.6б);

• рассчитать установившееся значение по формуле (4.9);

• составить рекуррентное разностное уравнение (4.8);

• составить таблицу, аналогичную приведенной таблице пошагового расчета 4.2;

• провести расчет переходного процесса в S-модели с соответствующими параметрами;

• используя результаты моделирования, сохраненные в память программы, построить график в среде Matlab так, чтобы сравнить найденные значения с результатами расчета S-модели.

Для этого, следует построить график в среде Matlab так, чтобы отдельные отсчеты «отстояли» друг от друга на интервал времени квантования. Это можно осуществить правильным указанием шага выборки из массива, который записан в память программы. Построение графиков следует выполнять без соединения линиями символов, фиксирующих отдельные отсчеты. Такой график будет в наиболее наглядной форме представлять поведение решетчатой функции x[n]. Далее необходимо указать координаты каждой из «дискрет» на плоскости графика, используя функции контекстного меню объекта figure (открытого окна графика Matlab), и, в заключение, сравнить с результатами пошагового расчета.

Так, например сравним результаты рекуррентного расчета с непосредственным моделированием дискретной системы в пакете Simulink при заданном значении времени квантования модели Т=0,2 с. Результаты записывались в двухколоночный массив R. Шаг времени расчета модели (Max step size) составлял 0,01 с, поэтому шаг выборки составляет 0,2/0,01=20 и синтаксис команды имеет вид:

plot(R(1:20:201,1),R(1:20:201,2),'ko').

Рис. 4.6. Результаты моделирования переходного процесса в пакете Simulink.

Результаты моделирования представлены на рис. 4.6. Для каждого из значений переходной функции непосредственно на графике указаны значения ее координат. Для этого в режиме Data Cursor (на панели Figure Toolbar) по каждой из точек графика производился щелчок ЛКМ при нажатой клавише Alt. Как видно из рис. 4.6 результаты моделирования совпадают с данными, приведенными в табл. 4.2.

В отчете должны быть представлены:

• структурная схема исследуемой импульсной системы;

• результаты расчета варьируемого параметра, соответствующего двум режимам работы импульсной системы (распечатку диалогового окна выполнения файла-сценария включать не следует!);

• переходной процесс в системе при настройке на два этих режима;

• анализ изменения переходного режима при изменениях варьируемых параметров системы;

• выражение для передаточной функции замкнутой системы с вычисленными значениями параметров;

• таблица результатов рекуррентного расчета переходного процесса с подтверждением в виде графика моделирования его;

• письменный ответ на вопросы, указанные преподавателем.