1. Линейные однородные уравнения 2-го порядка с постоянными коэффициентами.

1.1. Линейным однородным уравнением 2-го порядка с постоянными коэффициентами называется уравнение вида:

, (32)

где коэффициенты и - некоторые действительные числа.

1.2. Если и - линейно независимые решения уравнения (32), то функция , где и - произвольные постоянные, является общим решением уравнения.

1.3. Для нахождения частных решений уравнения (32) составляют характеристическое уравнение:

(33)

которое получается из уравнения (32) заменой в нем производных искомой функции соответствующими степенями , причем сама функция заменяется единой.

1.4. Уравнение (33) является уравнением 2-ой степени и имеет два корня

(действительных или комплексных, среди которых могут быть и равные).

Тогда общее решение дифференциального уравнения (32) стремится в зависимости от характера корней уравнения (33):

1) каждому действительному простому корню в общем решении соответствует слагаемое вида ; тогда общее решение уравнения (11) записывается следующим образом: , где , - произвольные постоянные, , - корни характеристического уравнения;

2) действительному корню кратности 2 в общем решении соответствует слагаемое вида , т.е. , где

и - постоянные, - корень характеристического уравнения ;

3) паре комплексных сопряженных корней и в общем решении соответствует слагаемое вида

, т.е.

2. Линейное неоднородное уравнение 2-го порядка с постоянными коэффициентами.

2.1. Линейное неоднородное уравнение 2-го порядка с постоянными коэффициентами, т.е. уравнение с правой частью, записывается в следующем виде:

2.2. Общее решение линейного неоднородного уравнения равно сумме любого его частного решения и общего решения соответствующего однородного уравнения , т.е.

2.3. Частное решение уравнения

надо искать в виде:

Во всех случаях за надо взять многочлен с буквенными коэффициентами, которые находятся после подстановки в уравнение методом неопределенных коэффициентов.

2.4. Частное решение уравнения

надо искать в виде:

если не корень

характеристического уравнения;

если простой корень

характеристического уравнения;

если двойной корень

характеристического уравнения.

Во всех случаях за надо взять многочлен с буквенными коэффициентами, которые определяться после подстановки в уравнение методом неопределенных коэффициентов.

2.5. Частное решение уравнения

надо искать в виде:

, если не корень характеристического уравнения;

, если корень характеристического уравнения.

Пример 1.

Найти общее решение дифференциального уравнения

и частное решение, удовлетворяющее начальным условиям:

, при

а) Найдем общее решение однородного уравнения

Характеристическое уравнение имеет два

равных корня . Тогда общее решение (второй вид):

б) Функцию - частное решение данного уравнения найдем методом неопределенных коэффициентов по виду правой части (пункт 2.4)

В нашем примере

Следовательно, , так как

Дифференцируя два раза и подставляя производные в данное уравнение, получим:

; ; ; ; .

Таким образом, , а общее решение данного уравнения

есть (34)

в) Найдем частное решение, удовлетворяющее начальным условиям:

; при

Продифференцируем общее решение (34) и получим:

,

(35)

Полагая , при , и получим систему уравнений (31) и (32) относительно неизвестных , и решим ее:

;

; ;

Следовательно, искомое частное решение имеет вид:

.

Пример 2.

Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям: , при

Общее решение данного уравнения имеет вид

а) Найдем - решение уравнения

Характеристическое уравнение имеет два различных вещественных корня и (первый вид).

Тогда

б) - частное решение данного уравнения, будем искать согласно пункту 2.5, где A=0, B=2

в виде:

Дифференцируя это равенство два раза и подставляя найденные производные в исходное уравнение, получим:

;

;

Т.е.

Таким образом:

или

Приравняем коэффициенты при , , получим систему уравнений относительно неизвестных M и N:

или

или

Решив систему получим: ;

Тогда имеем

Итак, общее решение исходного уравнения имеет вид:

Найдем частное решение уравнения, удовлетворяющее начальным условиям , при

Продифференцируем общее решение уравнения.

Имеем:

Полагая , при , получим систему уравнений

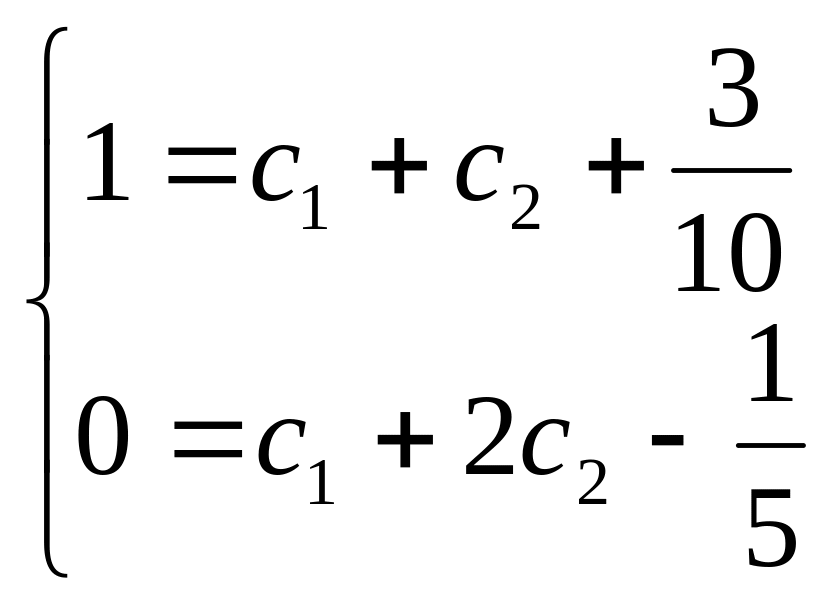
Решив ее имеем: ,

Следовательно, искомое частное решение уравнения имеет вид:

.

Пример 3.

Найти общее решение дифференциального уравнения

и частное решение, удовлетворяющее начальным условиям , при

Решение.

Характеристическое уравнение имеет вид:

Его корни: (третий вид, )

Тогда

Найдем частное решение по виду правой части (2.3), где

т.е. - многочлен второй степени.

Имеем:

Дифференцируя это равенство два раза и подставляя найденные производные и в исходное уравнение, получаем:

; ;

Раскроем скобки, приведем подобные члены и приравняем коэффициенты в обеих частях равенства при , , . В результате получается:

13A=1

13B+8A=0

13C+4B+2A=0

Откуда ;

; ;

; ; .

И следовательно,

Общее решение исходного уравнения:

Найдем частное решение уравнения, удовлетворяющее начальным условиям: , при

Продифференцируем общее решение уравнения, получим:

Полагая , при , получим систему уравнений:

Решив ее имеем: ,

Следовательно, искомое частное решение имеет вид

Задачи 81-90

Для решения задач №81-90 необходимо изучить следующие темы:

1. Числовые ряды. Сумма ряда [2] гл. XVI §1

2. Основные свойства сходящихся числовых рядов [2]гл. XVI §1

3. Необходимый признак сходимости [2] гл. XVI §2

4. Признак сравнения [2] гл. XVI §3

5. Признак Даламбера [2] гл. XVI §4

6. Признак Коши [2] гл. XVI §5

7. Интегральный признак Коши [2] гл. XVI §6

8. Знакочередующиеся ряды. Признак Лейбница [2] гл. XVI §7

9. Функциональные ряды. Область сходимости [2] гл. XVI §8

10. Степенные ряды. Интервал сходимости [2] гл. XVI §13

Указанные разделы учебников содержат следующие основные теоретические сведения

Основные теоретические сведения.