Основные теоретические знания
1.Площадь фигуры, ограниченной графиком непрерывной функции y=ƒ(x) (ƒ(x)≥0), прямыми x=a и x=b отрезком (a,b) оси OX или площадь криволинейной трапецией ограниченной дугой графика функции y=ƒ(x) , a≤x≤b (рис.2), вычисляется по формуле
(25) 
Рис. 5
2.Площадь фигуры ограниченной графиками непрерывных функций и , и двумя прямыми
x=a, x=b (рис.3) определяется по формуле
y
x
X=b
X=a
Рис.6
Рис. 3
Задача №1.
Вычислить
площадь фигуры ограниченной параболой
и прямой y=x+1
.
Найдем абциссы точек пересечения прямой y = x+1 с
параболой
Решая систему уравнений
Получаем
.
Это и есть пределы интегрирования.
Вершину параболы наёдем по формуле;
,
,
.
Найдем ординаты точек пересечения.
,
Имеем
(-1;0)
и (-7;8)
Построим фигуру.
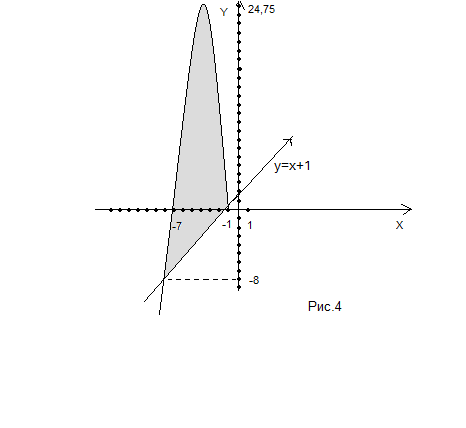
И
Ответ:Площадь
искоймой фигуры равна .
Задача №2.
Вычислить площадь фигуры ограниченной параболой
+5x-6
и прямой y=x+1
.
Найдем абциссы точек пересечения прямой
y=x+1 с параболой +5x-6
Решая систему уравнений
Для построения фигуры найдем координаты вершины параболы по формуле
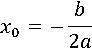
Найдем ординаты точек пересечения.
Имеем
(-1;0) и (-7;-8)
Построим фигуру.
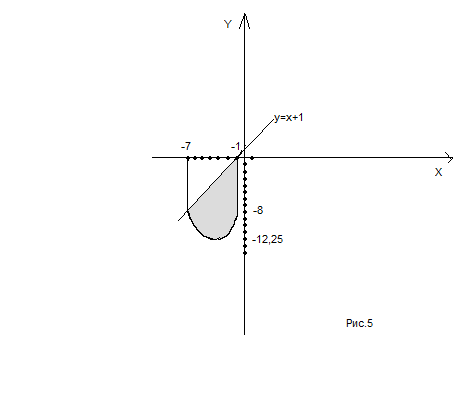
Искомая площадь фигуры согласно по формуле (5) такова:
Ответ:Площадь искомой фигуры равна .
Задачи 61-70
Для решения задач 61-70 необходимо изучить следующие темы:
1. Дифференциальные уравнения (общие понятия) [2] гл. XIII §2
2. Дифференциальные уравнения первого порядка [2] гл. XIII §3
3. Уравнения с разделяющимися переменными [2] гл. XIII §4
4. Однородные уравнения первого порядка [2] гл. XIII §5
5. Линейные уравнения первого порядка [2] гл. XIII §2
Указанные разделы учебников содержат следующие основные теоретические сведения
Основные теоретические сведения.
1. Дифференциальные уравнения (общие понятия).
1.1.
Дифференциальным уравнением называется
уравнение, содержащее независимую
переменную
,
неизвестную функцию
и
ее производные
,
,
… ,
1.2. Уравнение называется обыкновенным, если независимая переменная одна.
1.3. Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения.
1.4. Решением дифференциального уравнения называется функция
,
которая при подстановке в уравнение
вместо неизвестной функции обращает
его тождество. Процесс нахождения
решения дифференциального уравнения
называется интегрированием дифференциального
уравнения.
2. Дифференциальные уравнения первого порядка.
2.1.
Уравнение вида
или
(27)
называется дифференциальным уравнением первого порядка.
2.2. Задача Коши. Одной из важнейших задач в теории дифференциальных уравнений является так называемая задача Коши. Для уравнени задача Коши ставится следующим образом:
среди всех решений
уравнения (27) найти такое решение
,
(28)
в котором функция
принимает заданное числовое значение
при
заданном числовом значении
независимой
переменной
,
т.е.
(29)
где
и
заданные числа, так что решение (28)
удовлетворяет условиям:
при
Условия
при
(другая запись
) называются начальными
условиями
этого решения.
2.3.
Общим решением
дифференциального уравнения первого
порядка
в области
называется функция обладающая
следующими свойствами:
1) она является решением данного уравнения при любых значениях производной постоянной , принадлежащих некоторому множеству;
2) для любого
начального условия
такого, что
,
существует единственное
значение
,
при котором решение
удовлетворяет
заданному начальному условию.
Если общее решение
уравнения (27) задано в неявном виде
или
, то оно называется общим
интегралом
этого уравнения.