§ 12. Мода и медиана
1. Дан ряд распределения дискретной случайной величины
xi |
10 |
20 |
30 |
40 |
50 |
pi |
0,2 |
0,3 |
0,35 |
0,1 |
0,05 |
Найти моду.
2. Дана плотность вероятности непрерывной случайной величины
.
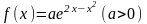Найти моду.
3.
Найти медиану случайной величины, если
известна плотность вероятности:
4.
Найти коэффициент a;
моду и медиану непрерывной случайной
величины с плотностью вероятности
(3/4; 3; 3)
§ 13. Законы распределения:
дискретные (биномиальное, Пуассона) и
непрерывные (равномерное, нормальное, показательное)
1. Бросают 3 монеты. Построить ряд распределения случайной величины X (число выпадений герба) и функцию распределения F(x).
2. С оптовой базы в магазин отправлено 5000 бутылок мин. воды. Вероятность того, что одна бутылка по пути разобьётся равна 0,0002. Найти вероятность, что разобьётся 3 бутылки. (1/6е 0,06)
3. Случайная величина X распределена равномерно на [a, b]; M(X)=6; D(X)=3. Найти её плотность распределения.
4. Мат. ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х равны 10 и 2 соответственно. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервал (12; 14). (0,1359)
Тема 4. Математическая статистика
§ 16. Статистическое распределение. Полигон и гистограмма
1. Задано распределение частот выборки объёма n = 60
xi 4 10 16 20 24 30
ni 15 18 6 4 5 12
Построить полигон частот, найти распределение относительных частот.
2. Исследовать репрезентативность выборки
xi 1 2 3 4 5 6
ni 1 1 3 4 11 5
для генеральной совокупности
xi 1 2 3 4 5 6
ni 4 6 12 16 44 18
3. Из большой группы предприятий одной из отраслей промышленности случайным образом отобрано 30, по которым получены показатели основных фондов (в млн. руб.): 3, 4, 2, 3, 3, 6, 5, 2, 4, 7, 5, 5, 3, 4, 3, 2, 6, 7, 5, 4, 3, 4, 5, 7, 6, 2, 3, 6, 6, 4. Составить дискретное статистическое распределение выборки, распределение относительных частот, построить полигон частот.
4. Найти интервальное статистическое распределение, частоты и относительные частоты для выборки, полученной при измерении электрической ёмкости двадцати пластин в пикофарадах по следующим результатам:
9,9; 11,0; 9,2; 12,0; 8,0; 8,7; 7,0; 11,8; 11,7; 10,3;
11,2; 8,1; 9,5; 11,5; 11,6; 9,7; 10,2; 11,4; 8,6; 10,0.
Построить гистограмму частот.
5. Выборочно обследовано 26 предприятий лёгкой промышленности по валовой продукции. Получены следующие результаты (в млн. руб.):
15,0; 16,4; 17,8; 18,0; 18,4; 19,2; 19,8; 20,2; 20,6; 20,6;
20,6; 21,3; 21,4; 21,7; 22,0; 22,2; 22,3; 22,7; 23,0; 24,2;
24,2; 25,1; 25,3; 26,0; 26,5; 27,1.
Составить интервальное распределение выборки с началом 15,0 и длиной частичного интервала 2,5. Построить гистограмму частот.
6. В результате испытания случайная величина Х приняла следующие значения:
2, 5, 7, 1, 10, 5, 9, 6, 8, 6, 2, 3, 7, 6, 8, 3, 8, 10, 6, 7, 3, 9, 4, 5, 6.
Требуется: 1) составить дискретное распределение выборки (таблицу зависимости значений случайной величины и частот); 2) составить распределение относительных частот; 3) построить полигон относительных частот.
7. В результате испытания случайная величина Х приняла следующие значения: 16, 17, 9, 13, 21, 11, 7, 7, 19, 5, 17, 5, 20, 18, 11, 4, 6, 22, 21, 15, 15, 23, 19, 25, 1. Требуется: 1) составить интервальное распределение, разбив отрезок [0, 25] на 5 промежутков одинаковой длины; 2) построить гистограмму относительных частот.