Тема 3. Случайные величины
§ 8. Дискретные и непрерывные величины.
1. Даны вероятности значений случайной величины X: значение 10 имеет вероятность 0,3; 2 — 0,4; 8 — 0,1; 4 — 0,2. Построить ряд распределения случайной величины и полигон.
2. Стрелок производит по мишени 3 выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения числа попаданий.
§ 9. Функция распределения и плотность распределения вероятности
1. Случайная величина X задана функцией распределения
.
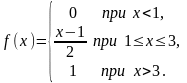Найти вероятности попадания X в интервалы (1,5; 2,5), (2,5; 3,5).
2. Случайная величина X задана функцией распределения
.
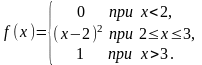Найти вероятности попадания X в интервалы (1; 2,5), (2,5; 3,5).
3. Дан ряд распределения случайной величины X:
xi |
10 |
20 |
30 |
40 |
50 |
pi |
0,2 |
0,3 |
0,35 |
0,1 |
0,05 |
Найти функцию распределения вероятности это случайной величины. Построить график.
4.
Случайная величина X
подчинена закону распределения
Требуется: 1) найти коэффициент a;
2) построить график плотности вероятности
f(x);
3) найти вероятность попадания X
в промежуток (1; 2).
Ответ: а=2/9; p=13/27.
5. В корзине 6 шаров, из которых 4 белых и 2 чёрных. Вынимают 3 шара. Случайной величиной является число белых шаров при вынимании. Для данной случайной величины 1) составить ряд распределения; 2) построить полигон; 3) найти функцию распределения и построить её график; 4) найти вероятность события 0,5<X<2,5.
§ 10, 11. Математическое ожидание и дисперсия
1. Найти мат. ожидание и дисперсию случайной величины X с рядом распределения
xi |
0 |
1 |
2 |
3 |
4 |
pi |
0,2 |
0,4 |
0,3 |
0,08 |
0,02 |
(M(X)=1,32; D(X)=0,897)
2.
Показать, что функция
может служить плотностью вероятности
некоторой случайной величины X.
Найти M(X),
D(X).
(D(X)0,69)
3. Заданы две независимые случайные величины X, Y. Величина X – дискретная, её ряд распределения
xi |
-2 |
-1 |
0 |
2 |
pi |
0,2 |
0,3 |
0,05 |
0,45 |
Величина
Y
– непрерывная с плотностью
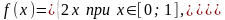
Найти мат. ожидание и дисперсию случайной величины Z=2X-3Y.
Ответ: -0,6; 12,69.
4. Найти D(X), если M(X)=1,5,
xi |
-2 |
-1 |
0 |
1,5 |
8 |
pi |
0,2 |
0,1 |
0,2 |
P4 |
P5 |
5. Производится 3 независимых опыта, в каждом из которых событие А появляется с вероятностью 0,4. Случайной величиной X является число появлений события А в трёх опытах. Построить ряд распределения и функцию распределения для X. Найти мат. ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение (X).
Ответ: 1,2; 0,72; 0,85.
6.
Найти 1) коэффициент a;
2) интегральную функцию распределения
F(x);
3) вероятность попадания X
в промежуток (5,5; 9) 4) мат. ожидание M(X);
5) дисперсию D(X);
6) построить графики f(x)
и
F(x),
если
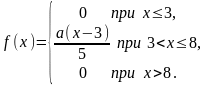
Ответ: a =0,4; p=3/4; M=19/3; D=25/18.