§ 6. Формула Байеса
где
|
,
Д/з 1. В цехе 60 ящиков с исправными деталями и 20 – с бракованными. Среди исправленных деталей 80% отникелированы, а из бракованных – 10%. Вынутая наугад деталь оказалась отникелирована. Найти вероятность того, что она исправна. (0,96)
Д/з 2. Есть 5 урн с белыми и чёрными шарами: в двух урнах – по 2 белых и 3 чёрных шара; ещё в двух урнах – по одному белому и 4 чёрных шара; а в одной – 4 белых и 1 чёрный шар. Из одной наудачу выбранной урны извлечён шар, который оказался чёрным. Найти вероятность того, что он из урны, в которой 1 белый и 4 чёрных шара. (8/15)
3. Известно, что 96% выпускаемой продукции удовлетворяет стандарту. Упрощённая схема контроля признаёт пригодной стандартную продукцию с вероятностью 0,98 и нестандартную – с вероятностью 0,05. Найти вероятность того, что изделие прошедшее упрощённый контроль, удовлетворяет стандарту. (0,998)
4. Предположим, что 5% всех мужчин и 0,25% всех женщин дальтоники. Наугад выбранное лицо оказалось дальтоником. Найти вероятность того, что это мужчина. (Считать, что количество мужчин и женщин одинаково.) (20/21)
5. Счётчик регистрирует частицы трёх типов – А, В, С. Вероятность появления этих частиц Р(А)=0,2; Р(В)=0,5; Р(С)=0,3. Частицы каждого из этих типов счётчик улавливает с вероятностями Р1=0,8; Р2=0,2; Р3=0,4. Счётчик отметил частицу. Найти вероятность того, что это была частица В. (0,2632)
6. Предохранитель в электронной цепи отказывает при коротком замыкании в электронной лампе с вероятностью 0,4; при замыкании в обмотке трансформатора – с вероятностью 0,6; при пробое конденсатора – с вероятностью 0,8; по другим причинам – с вероятностью 0,3. Априорные вероятности событий соответственно – 0,25; 0,15; 0,32; 0,28. Найти наиболее вероятную причину отказа предохранителя после того, как такое событие произошло. (3)
7. Имеется 10 одинаковых урн, из которых в 9 находятся по 2 чёрных и по 2 белых шара, а в одной – 5 белых и 1 чёрный шар. Из урны, выбранной наугад, извлечён белый шар. Найти вероятность того, что шар извлечён из урны, содержащей 5 белых шаров. (5/32)
8. У рыбака есть 3 любимых места для ловли рыбы, которые он посещает с равной вероятностью каждое. Если он закидывает удочку на первом месте, рыба клюёт с вероятностью 0,1; на втором – 0,2; на третьем – 0,2. Известно, что рыбак, выйдя на ловлю рыбы, 3 раза закинул удочку и рыба клюнула только 1 раз. Найти вероятность того, что он удил рыбу на первом месте.
§ 7. Формула Бернулли
Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна р, то вероятность того, что событие А появится в этих n испытаниях k раз выражается формулой Бернулли:
причём Pn(0)+Pn(1)+Pn(2)+…+Pn(n)=1. Вероятность того, что при n независимых испытаниях событие А наступит хотя бы 1 раз, вычисляется по формуле Pn(k≥1)=1 qn. Вероятность того, что при n независимых испытаниях событие А наступит не менее m раз, вычисляется по формуле Pn(k≥m)= Наивероятнейшее значение m числа появлений события в независимых испытаниях определяется из неравенства
|
,
,
.
.
Д/з 1. По мишени производится 7 выстрелов, причём вероятность попадания при каждом выстреле равна 0,7. Найти вероятность того, что мишень будет поражена тремя выстрелами. (0,972)
Д/з 2. При каждом взвешивании возможно как положительная таки отрицательная ошибка. Найти вероятность того, что при пяти взвешиваниях получатся 3 положительные ошибки. (0,3125)
3. Для данного баскетболиста вероятность забросить мяч в корзину при каждом броске равна 0,4. Что вероятнее ожидать: попадания трёх мячей при четырёх бросках или четырёх при шести. (1)
4. В Магазине 11 покупателей. Вероятность совершить покупку каждым их них равна 0,1. Найти вероятность того, что 7 из них совершат покупку. (22.10-6)
5. В урне 20 белых и 10 чёрных шаров. Вынули подряд 4 шара, причём каждый шар снова вернули в урну. Найти вероятность того, что из четырёх вынутых шаров 2 белых. (8/27)
6. В семье 5 детей. Найти вероятность того, что среди них не более трёх девочек. (13/16)
7. Вероятность солнечной погоды для каждого дня равна 0,4. Найти вероятность того, что в течении трёх дней хотя бы 1 день солнечный. (0,784)
8. Стрелок стреляет по мишени 4 раза. Вероятность попадания в цель при каждом выстреле равна 0,6. Найти вероятность того, что произойдёт не менее трёх попаданий. (0,4752)
9. Производится 8 выстрелов по резервуару с горючим. Первое попадание вызывает течь, второе – воспламенение. Найти вероятность того, что резервуар будет подожжён, если вероятность попадания при отдельном выстреле равна 0,2. (0,497)
10. Вероятность поражения мишени лучником при одном выстреле из лука р=0,75. Найти вероятность того, что при 5 выстрелах лучник поразит мишень 3 раза. (0,2637)
11. Событие А состоит в одновременном выпадении двух гербов при бросании трёх монет. Найти вероятность события А. (3/8)
12. Что вероятнее: выиграть у равного по силам противника (ничья исключена) 3 партии из 4 или 5 из 8?
13. В зрительном зале кинотеатра подачу воздуха обеспечивают 6 вентиляторов. Для каждого вентилятора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 вентилятора; б) включены все вентиляторы; в) выключены все вентиляторы. (0,246; 0,26; 0,000064)
14. Вероятность попадания в цель при выстреле из миномёта равна 0,3. Найти вероятность того, что при 5 выстрелах будет не менее двух попаданий в цель. (0,472)
15. Монету бросают 6 раз. Найти вероятность того, что герб выпадет: а) менее 2 раз; б) не менее двух раз. (7/64; 57/64)
16. Проведено 10 независимых испытаний, каждое из которых заключается в одновременном подбрасывании 3 игральных кубиков. Найти вероятность того, что в 4 испытаниях появятся в точности по две единицы. (0,0317)
17. Проводится тестирование студентов. В каждом билете по 5 вопросов. На каждый вопрос даны 3 возможных ответа, среди которых нужно выбрать один правильный. Найти вероятность того, что методом простого угадывания удастся ответить как минимум на 4 вопроса. (0,04527)
18. Две электрические лампочки включены в сеть последовательно. Найти вероятность того, что при повышении напряжения в сети выше номинального произойдёт разрыв цепи, если вероятность того, что лампочка перегорит, для обеих лампочек одинакова и равна 0,4. (0,64)
19. Сервисная компьютерная компания обслуживает 10 организаций, от каждой из которых может поступить заявка на очередной день с вероятностью 0,4, независимо от заявки других организаций. Найти наивероятнейшее число заявок в день и вероятность получения этого числа заявок. (4; 0,251)
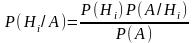
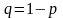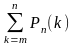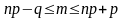