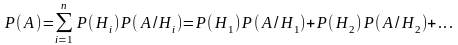§ 5. Формула полной вероятности

1. Из 50 изделий 18 изготовлено в первом цехе, 20 – во втором, остальные – в третьем. Первый и третий цеха дают продукцию отличного качества с вероятностью 0,9, а второй – 0,6. Найти вероятность того, что взятое наугад изделие будет отличного качества. (0,78)

2. Есть 3 набора радиоламп, первый из которых содержит 100 ламп, второй – 300, третий – 600. Вероятность, что лампа, взятая наугад из 1-го набора, стандартна равна 0,9; из второго – 0,85; из третьего – 0,8. Найти вероятность того, что произвольно выбранная лампа стандартна. (0,825)

3. Студент К. знает не все билеты. Что для него выгодней: отвечать первым или вторым?

4. В первую команду шахматистов вошли 7 гроссмейстеров и 3 мастера спорта, во вторую – 4 гроссмейстера и 6 мастеров спорта. Сборная, составленная из двух команд, состоит из 10 человек: 8 человек из 1-й команды и 2 человека из 2-й. Из сборной наугад выбирается шахматист. Найти вероятность того, что он гроссмейстер. (0,64)

5. Есть 5 урн с цветными шарами: в двух урнах по 3 белых и 4 чёрных шара, в одной урне 10 белых шаров, а в двух остальных по 2 белых и 5 чёрных шаров. Наудачу выбирается урна, а из неё извлекается шар. Найти вероятность того, что извлечён чёрный шар. (18/35)

6. В урне 20 шаров, из которых 8 белых. Один шар укатился, и цвет его неизвестен. Вынимают один шар из оставшихся. Найти вероятность того, что он будет белым. (0,4)

7. По цели произведено 3 последовательных выстрела. Вероятность попадания при первом выстреле 0,5; при втором – 0,6; при третьем – 0,8. При одном попадании вероятность поражения цели равна 0,4; при двух – 0,7; при трёх – 1,0. Найти вероятность поражения цели при трёх выстрелах. (0,666)

Д/з 8. Два предприятия изготавливают однотипные детали. Первое предприятие даёт 10% брака, второе – 15%. Для контроля отобрано 20 деталей первого предприятия и 30 – второго. Детали смешаны в одну партию и из неё случайным образом отобрана одна деталь Найти вероятность того, что она бракованная. (0,13)

Д/з 9. Техническое устройство работает 50% времени в первом режиме, 20% – во втором, 30% – в третьем. Надёжность (вероятность безотказной работы) устройства при работе в первом режиме 0.8, во втором – 0,9, в третьем – 0,7. Найти полную надёжность технического устройства. (0,79)

Д/з 10. В первой урне 1 белый и 4 чёрных шара, а во второй – 1 белый и 7 чёрных шаров. В первую урну добавляют 2 шара, извлечённых из второй урны наугад. Найти вероятность того, что шар, наугад извлечённый из пополненной урны, будет белым. (5/28)

11. В первой урне находятся 3 белых и 5 чёрных шаров, во второй – 5 белых и 8 чёрных, в третьей – 8 белых и 4 чёрных. Случайным образом выбирают урну и наугад достают из неё 2 шара. Найти вероятность того, что оба шара белые. (0,2198)

Д/з 12. В первой урне находятся 3 белых и 5 чёрных шаров, во второй – 5 белых и 8 чёрных, в третьей – 8 белых и 4 чёрных. Случайным образом выбирают урну и наугад достают из неё 2 шара. Найти вероятность того, что шары разных цветов. (0,255)

13. В магазин поступают мобильные телефоны от трёх различных производителей. Продукция первой фирмы содержит 5% телефонов со скрытым дефектом, второй – 3%, третьей – 2%. Найти вероятность приобретения исправного телефона, если в магазин поступило 40% телефонов от первого производителя, 25% – от второго и 35% – от третьего. (0,9655)

14. Группа студентов состоит из 5 отличников, 10 хорошистов и 10 троечников. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошисты могут получить с равной вероятностью хорошие и отличные оценки. Троечники могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена наугад вызывается 1 студент. Найти вероятность того, что он получит хорошую или отличную оценку. (0,7333)

15. По цели производится 3 независимых выстрела. Вероятность попадания в цель при первом выстреле равна 0,1; при втором – 0,2; при третьем – 0,3. Для поражения цели достаточно двух попаданий, при одном попадании цель поражается с вероятностью 0,6. Найти вероятность поражения цели. (0,3368)

Д/з 16. В одной урне 5 белых и 5 чёрных шаров, а в другой – 4 белых и 7 чёрных. Из первой урны случайным образом вынимают 2 шара и опускают во вторую урну. После этого из второй урны также случайно вынимают 3 шара. Найти вероятность того, что все шары, вынутые из второй урны, белые. (0,038)